Przez wierzchołek kąta prostego trójkąta prostokątnego o przyprostokątnych 5 i 12 poprowadzono prostą, która dzieli ten trójkąt na dwa trójkąty o równych obwodach. Znajdź stosunek promieni okręgów wpisanych w otrzymane z podziału trójkąty.
/Konkursy/Zadania/Geometria/Planimetria/Trójkąt/Prostokątny
Przez wierzchołek kąta prostego trójkąta prostokątnego o przyprostokątnych 8 i 15 poprowadzono prostą, która dzieli ten trójkąt na dwa trójkąty o równych obwodach. Znajdź stosunek promieni okręgów wpisanych w otrzymane z podziału trójkąty.
Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek 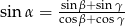 to trójkąt ten jest prostokątny.
to trójkąt ten jest prostokątny.
Trójkąt prostokątny 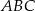 ma boki długości 3, 4, 5. Oblicz promień okręgu stycznego do przeciwprostokątnej i prostych będących przedłużeniami przyprostokątnych.
ma boki długości 3, 4, 5. Oblicz promień okręgu stycznego do przeciwprostokątnej i prostych będących przedłużeniami przyprostokątnych.
Punkt 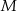 przyprostokątnej
przyprostokątnej 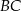 trójkąta prostokątnego
trójkąta prostokątnego 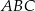 zrzutowano na przeciwprostokątną
zrzutowano na przeciwprostokątną 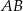 otrzymując punkt
otrzymując punkt 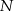 . Wykaż, że
. Wykaż, że 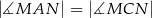 .
.
Wykaż, że w trójkącie prostokątnym suma długości obu przyprostokątnych jest równa sumie długości średnic okręgów wpisanego i opisanego na tym trójkącie.
Przyprostokątne trójkąta prostokątnego mają długości  i
i 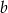 , a jego przeciwprostokątna ma długość
, a jego przeciwprostokątna ma długość  . Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość
. Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość 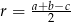 .
.
Oblicz jaka może być najmniejsza możliwa długość przeciwprostokątnej trójkąta prostokątnego o polu 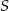 .
.
Okrąg wpisany w trójkąt prostokątny 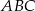 o bokach długości
o bokach długości 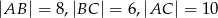 jest styczny do boków
jest styczny do boków 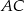 i
i 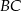 w punktach
w punktach 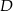 i
i 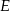 . Proste
. Proste 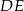 i
i 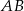 przecinają się punkcie
przecinają się punkcie 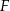 . Oblicz pole trójkąta
. Oblicz pole trójkąta 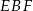 .
.
Na przyprostokątnych 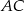 i
i 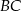 trójkąta prostokątnego
trójkąta prostokątnego 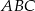 zbudowano, na zewnątrz trójkąta, kwadraty
zbudowano, na zewnątrz trójkąta, kwadraty 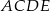 i
i 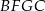 . Odcinek
. Odcinek 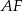 przecina przyprostokątną
przecina przyprostokątną 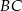 w punkcie
w punkcie 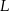 , a odcinek
, a odcinek 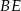 przecina przyprostokątną
przecina przyprostokątną 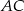 w punkcie
w punkcie 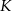 (zobacz rysunek). Udowodnij, że
(zobacz rysunek). Udowodnij, że 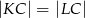 .
.
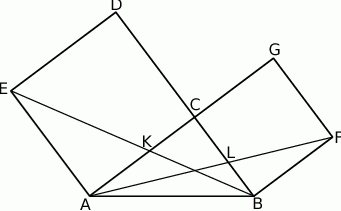
Na przyprostokątnych 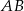 i
i 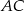 trójkąta prostokątnego równoramiennego
trójkąta prostokątnego równoramiennego 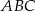 zaznaczono odpowiednio punkty
zaznaczono odpowiednio punkty 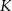 i
i 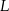 tak, że
tak, że 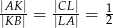 . Odcinki
. Odcinki 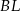 i
i 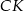 przecinają się w punkcie
przecinają się w punkcie 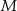 . Oblicz
. Oblicz 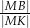 .
.
Przez środek 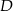 przyprostokątnej
przyprostokątnej 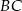 trójkąta prostokątnego
trójkąta prostokątnego 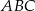 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 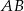 . Prosta ta przecina proste
. Prosta ta przecina proste 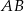 i
i 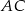 odpowiednio w punktach
odpowiednio w punktach 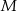 i
i 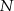 . Wykaż, że
. Wykaż, że 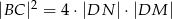 .
.
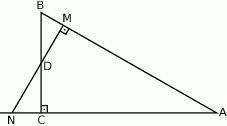
Przez środek 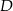 przyprostokątnej
przyprostokątnej 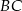 trójkąta prostokątnego
trójkąta prostokątnego 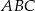 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 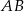 . Prosta ta przecina proste
. Prosta ta przecina proste 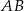 i
i 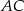 odpowiednio w punktach
odpowiednio w punktach 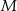 i
i 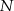 . Wykaż, że skala podobieństwa trójkątów
. Wykaż, że skala podobieństwa trójkątów 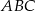 i
i 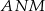 jest równa
jest równa 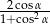 .
.
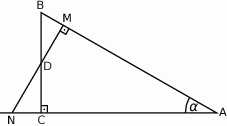
W trójkącie prostokątnym 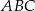 o kącie prostym w wierzchołku
o kącie prostym w wierzchołku 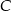 obrano taki punkt
obrano taki punkt 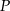 , że pola trójkątów
, że pola trójkątów 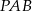 ,
, 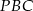 i
i 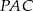 są równe. Oblicz długość odcinka
są równe. Oblicz długość odcinka 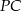 , wiedząc, że
, wiedząc, że 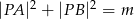 .
.
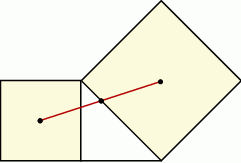
Na zewnątrz równoramiennego trójkąta prostokątnego zbudowano kwadraty – jeden na przyprostokątnej, a drugi na przeciwprostokątnej. Wykaż, że przeciwprostokątna dzieli odcinek łączący środki kwadratów na dwie równe części.
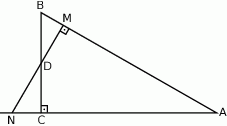
Przez środek 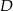 przyprostokątnej
przyprostokątnej 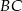 trójkąta prostokątnego
trójkąta prostokątnego 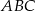 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 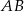 . Prosta ta przecina proste
. Prosta ta przecina proste 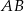 i
i 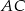 odpowiednio w punktach
odpowiednio w punktach 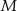 i
i 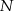 . Wykaż, że
. Wykaż, że 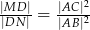 .
.
Środkowa trójkąta jest równa połowie boku, do którego została poprowadzona. Wykaż, że trójkąt ten jest prostokątny.
Wysokość trójkąta prostokątnego poprowadzona do przeciwprostokątnej ma długość 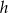 i jest pięć razy krótsza od obwodu tego trójkąta. Oblicz długości boków trójkąta.
i jest pięć razy krótsza od obwodu tego trójkąta. Oblicz długości boków trójkąta.

