Oblicz obwód trójkąta o wierzchołkach: 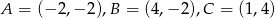 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Dane są trzy wierzchołki
Oblicz obwód trójkąta o wierzchołkach: 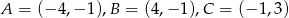 .
.
Wyznacz współrzędne środka ciężkości trójkąta w zależności od współrzędnych jego wierzchołków.
Punkty 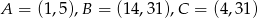 są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka 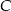 przecina prostą
przecina prostą 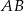 w punkcie
w punkcie 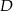 . Oblicz długość odcinka
. Oblicz długość odcinka 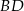 .
.
Punkty 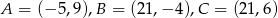 są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka 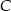 przecina prostą
przecina prostą 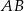 w punkcie
w punkcie 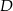 . Oblicz długość odcinka
. Oblicz długość odcinka 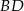 .
.
Dane są punkty 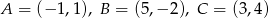 .
.
- Wyznacz równanie prostej przechodzącej przez punkt
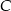 i prostopadłej do prostej
i prostopadłej do prostej 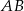 .
. - Oblicz pole trójkąta
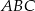 .
.
Wierzchołki trójkąta 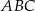 mają współrzędne:
mają współrzędne: 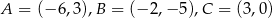 . Okrąg
. Okrąg  jest styczny do prostej
jest styczny do prostej 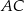 , a jego środek jest punktem przecięcia się wysokości trójkąta
, a jego środek jest punktem przecięcia się wysokości trójkąta 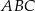 . Okrąg
. Okrąg  przecina prostą
przecina prostą 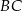 w punkcie
w punkcie 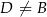 . Oblicz iloraz
. Oblicz iloraz 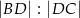 .
.
Wierzchołki trójkąta 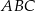 mają współrzędne:
mają współrzędne: 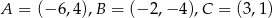 . Napisz równanie okręgu, który jest styczny do prostej
. Napisz równanie okręgu, który jest styczny do prostej 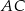 , a jego środek jest punktem przecięcia się wysokości trójkąta
, a jego środek jest punktem przecięcia się wysokości trójkąta 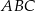 .
.
Dane są wierzchołki trójkąta 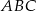 :
: 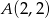 ,
, 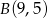 i
i 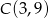 . Z wierzchołka
. Z wierzchołka 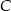 poprowadzono wysokość tego trójkąta, która przecina bok
poprowadzono wysokość tego trójkąta, która przecina bok 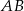 w punkcie
w punkcie 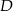 . Wyznacz równanie prostej przechodzącej przez punkt
. Wyznacz równanie prostej przechodzącej przez punkt 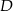 i równoległej do boku
i równoległej do boku 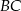 .
.
Wierzchołkami trójkąta 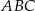 są punkty
są punkty 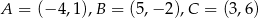 . Oblicz długość środkowej
. Oblicz długość środkowej 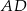 .
.
Wierzchołkami trójkąta 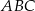 są punkty
są punkty 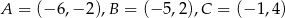 . Oblicz długość środkowej
. Oblicz długość środkowej 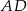 .
.
Dany jest trójkąt 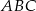 o wierzchołkach
o wierzchołkach 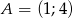 ,
, 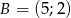 ,
, 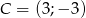 .
.
- Napisz równanie wysokości opuszczonej z wierzchołka
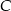 na bok
na bok 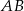 .
. - Napisz równanie środkowej boku
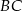 .
. - Napisz równanie symetralnej boku
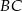 .
. - Oblicz obwód i pole tego trójkąta.
Przekształcenie 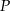 określone jest w następujący sposób:
określone jest w następujący sposób: 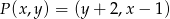 , gdzie
, gdzie 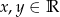 .
.
- Wykaż, że przekształcenie
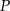 jest izometrią.
jest izometrią. - W prostokątnym układzie współrzędnych narysuj trójkąt o wierzchołkach
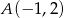 ,
, 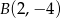 ,
, 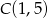 , a następnie znajdź jego obraz w przekształceniu
, a następnie znajdź jego obraz w przekształceniu 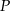 .
. - Wyznacz równanie prostej zawierającej wysokość trójkąta
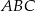 poprowadzoną na bok
poprowadzoną na bok 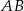 .
. - Oblicz pole trójkąta
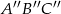 , który jest obrazem trójkąta
, który jest obrazem trójkąta 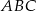 w jednokładności o środku w punkcie (0,0) i skali
w jednokładności o środku w punkcie (0,0) i skali 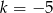 .
.