Wierzchołkami kwadratu  są punkty o współrzędnych
są punkty o współrzędnych 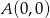 ,
, 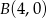 ,
, 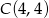 i
i 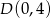 . Dla każdej liczby rzczywistej
. Dla każdej liczby rzczywistej 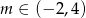 rozważamy trójkąt o wierzchołkach
rozważamy trójkąt o wierzchołkach 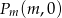 ,
, 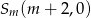 i
i 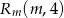 . Wyznacz wszystkie wartości prametru
. Wyznacz wszystkie wartości prametru 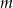 , dla których pole figury, która jest częścią wspólną kwadratu
, dla których pole figury, która jest częścią wspólną kwadratu 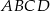 i trójkąta
i trójkąta 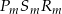 wynosi 2.
wynosi 2.

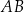 trójkąta
trójkąta 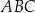 o wierzchołkach
o wierzchołkach 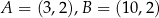 i
i 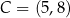 .
. 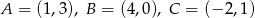 .
. 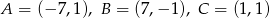 opuszczonej z wierzchołka
opuszczonej z wierzchołka 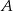 .
. 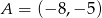 ,
, 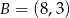 i
i 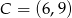 .
. 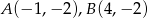 oraz
oraz 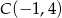 .
. 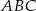 .
. 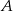 od prostej
od prostej 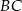 .
. 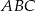 .
. 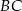 .
. .
.  .
. 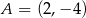 ,
, 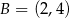 i
i 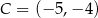 są wierzchołkami trójkąta
są wierzchołkami trójkąta 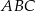 . Napisz równanie prostej zawierającej tą średnicę okręgu opisanego na trójkącie
. Napisz równanie prostej zawierającej tą średnicę okręgu opisanego na trójkącie 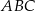 , której końcem jest punkt
, której końcem jest punkt 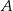 .
. 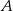 trójkąta
trójkąta 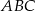 o wierzchołkach
o wierzchołkach 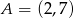 ,
, 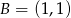 i
i 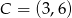 na środkową
na środkową 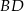 boku
boku 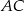 .
.  , gdzie
, gdzie  .
. 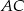 .
. 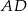 .
. 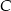 .
. 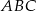 , gdzie
, gdzie 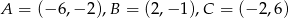 .
. 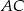 .
. 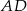 .
. 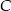 .
. 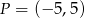 jest środkiem okręgu wpisanego w trójkąt o wierzchołkach
jest środkiem okręgu wpisanego w trójkąt o wierzchołkach 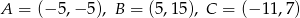 .
. 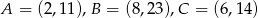 są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka 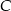 przecina prostą
przecina prostą 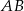 w punkcie
w punkcie 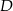 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 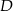 .
. 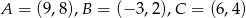 są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka 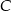 przecina prostą
przecina prostą 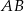 w punkcie
w punkcie 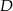 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 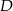 .
. 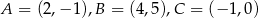 .
. 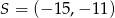 i promieniu
i promieniu 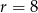 jest w całości zawarte w trójkącie o wierzchołkach
jest w całości zawarte w trójkącie o wierzchołkach 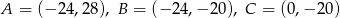 .
. 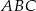 i trójkąt
i trójkąt 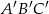 są przystające jeśli współrzędne ich wierzchołków to
są przystające jeśli współrzędne ich wierzchołków to 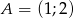 ,
, 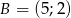 ,
, 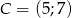 ,
, 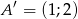 ,
, 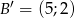 ,
, 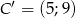 .
. 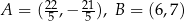 oraz
oraz 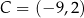 są wierzchołkami trójkąta
są wierzchołkami trójkąta 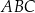 . Symetralna boku
. Symetralna boku 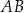 tego trójkąta przecina bok
tego trójkąta przecina bok 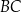 w punkcie
w punkcie 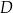 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 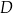 .
. 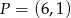 leży na dwusiecznej kąta
leży na dwusiecznej kąta 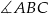 trójkąta o wierzchołkach
trójkąta o wierzchołkach 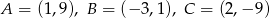 .
. 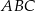 o wierzchołkach:
o wierzchołkach: 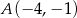 ,
, 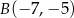 ,
, 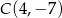 . Oblicz długość odcinka
. Oblicz długość odcinka 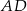 dwusiecznej kąta przy wierzchołku
dwusiecznej kąta przy wierzchołku 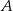 .
. 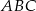 o wierzchołkach
o wierzchołkach 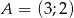 ,
, 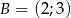 ,
, 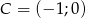 .
. 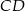 trójkąta
trójkąta 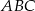 , którego wierzchołkami są punkty:
, którego wierzchołkami są punkty: 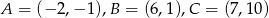 .
. 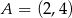 ,
, 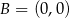 ,
, 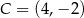 są wierzchołkami trójkąta
są wierzchołkami trójkąta 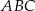 . Punkt
. Punkt 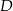 jest środkiem boku
jest środkiem boku 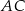 tego trójkąta. Wyznacz równanie prostej
tego trójkąta. Wyznacz równanie prostej 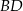 .
. 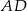 trójkąta
trójkąta 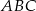 o wierzchołkach
o wierzchołkach 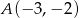 ,
, 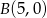 i
i 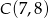 .
.  trójkąta
trójkąta 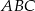 , którego wierzchołkami są punkty:
, którego wierzchołkami są punkty: 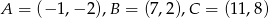 .
. 