Współrzędne przeciwległych wierzchołków prostokąta 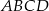 są równe
są równe 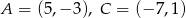 . Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek
. Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek 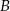 leży na prostej
leży na prostej 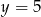 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Prostokąt
Punkt 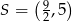 jest środkiem symetrii prostokąta
jest środkiem symetrii prostokąta 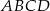 , którego pole jest równe 30, a bok
, którego pole jest równe 30, a bok 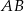 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 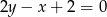 . Oblicz współrzędne wierzchołków prostokąta
. Oblicz współrzędne wierzchołków prostokąta 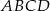 .
.
Dane są dwa przeciwległe wierzchołki 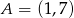 i
i 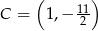 prostokąta
prostokąta 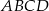 . Prosta o równaniu
. Prosta o równaniu 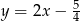 jest osią symetrii tego prostokąta. Oblicz współrzędne wierzchołków
jest osią symetrii tego prostokąta. Oblicz współrzędne wierzchołków 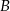 i
i 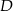 tego prostokąta.
tego prostokąta.
Dane są dwa wierzchołki 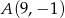 i
i 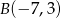 prostokąta
prostokąta 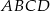 oraz punkt
oraz punkt 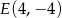 należący do boku CD.
należący do boku CD.
- Wyznacz równanie prostej zawierającej bok
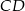 ;
; - Oblicz współrzędne wierzchołka C;
- Oblicz współrzędne punktu
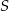 przecięcia się przekątnych tego prostokąta.
przecięcia się przekątnych tego prostokąta.
Punkty 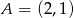 i
i 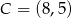 są przeciwległymi wierzchołkami prostokąta, którego bok
są przeciwległymi wierzchołkami prostokąta, którego bok 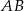 jest równoległy do osi
jest równoległy do osi 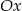 . Punkty
. Punkty 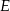 i
i 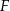 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 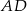 i
i 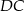 . Oblicz pole trójkąta
. Oblicz pole trójkąta 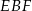 .
.
Dane są punkty 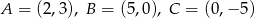 .
.
- Uzasadnij, że proste
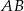 i
i 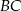 są prostopadłe.
są prostopadłe. - Wyznacz współrzędne takiego punktu
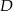 , dla którego czworokąt
, dla którego czworokąt 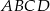 jest prostokątem.
jest prostokątem. - Oblicz pole prostokąta
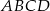 .
.
W prostokącie 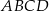 dane są
dane są 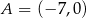 ,
, 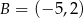 i
i 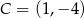 . Napisz równanie prostej, która jest styczna w punkcie
. Napisz równanie prostej, która jest styczna w punkcie 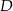 do okręgu opisanego na prostokącie
do okręgu opisanego na prostokącie 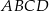 .
.
Dane są dwa wierzchołki 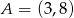 i
i 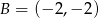 prostokąta
prostokąta 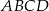 oraz punkt
oraz punkt 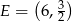 leżący na prostej
leżący na prostej 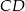 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 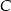 i
i 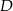 tego prostokąta.
tego prostokąta.
Wyznacz równanie okręgu opisanego na prostokącie 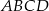 , w którym
, w którym 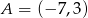 i
i 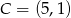 .
.
Przekątne prostokąta 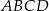 o polu
o polu 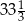 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 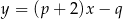 i
i 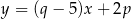 . Ponadto prosta
. Ponadto prosta 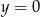 jest osią symetrii tego prostokąta. Oblicz obwód tego prostokąta.
jest osią symetrii tego prostokąta. Oblicz obwód tego prostokąta.
Przekątne prostokąta 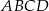 o obwodzie
o obwodzie 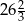 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 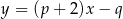 i
i 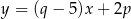 . Ponadto prosta
. Ponadto prosta 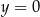 jest osią symetrii tego prostokąta. Oblicz pole tego prostokąta.
jest osią symetrii tego prostokąta. Oblicz pole tego prostokąta.
Dany jest prostokąt o wierzchołkach 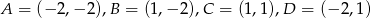 . Wyznacz wszystkie wartości współczynnika
. Wyznacz wszystkie wartości współczynnika 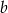 , dla których prosta o równaniu
, dla których prosta o równaniu 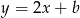 ma co najmniej jeden punkt wspólny z prostokątem
ma co najmniej jeden punkt wspólny z prostokątem 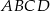 .
.

