W trójkącie ostrokątnym 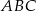 dane są
dane są 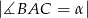 i
i 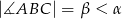 . Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka
. Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka 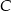 jest równy
jest równy
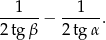
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie ostrokątnym 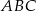 dane są
dane są 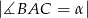 i
i 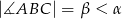 . Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka
. Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka 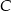 jest równy
jest równy
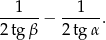
Na boku 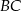 trójkąta
trójkąta 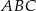 wybrano punkt
wybrano punkt 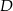 tak, by
tak, by 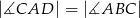 . Odcinek
. Odcinek 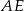 jest dwusieczną kąta
jest dwusieczną kąta 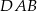 . Udowodnij, że
. Udowodnij, że 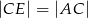 .
.
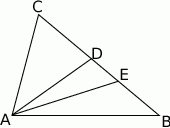
Na bokach 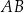 i
i 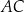 trójkąta
trójkąta 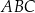 wybrano odpowiednio punkty
wybrano odpowiednio punkty 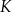 i
i 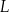 w ten sposób, że
w ten sposób, że 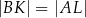 . Punkt
. Punkt 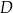 jest środkiem odcinka
jest środkiem odcinka 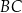 . Przez punkty
. Przez punkty 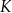 i
i 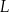 poprowadzono proste równoległe do
poprowadzono proste równoległe do 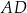 , które wyznaczyły na boku
, które wyznaczyły na boku 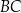 punkty
punkty 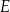 i
i 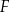 odpowiednio (zobacz rysunek). Wykaż, że jeżeli
odpowiednio (zobacz rysunek). Wykaż, że jeżeli 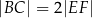 , to
, to 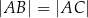 .
.

Punkty 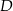 i
i 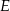 są środkami boków
są środkami boków 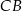 i
i 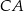 trójkąta
trójkąta 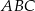 (zobacz rysunek). Wykaż, że odległość punktu
(zobacz rysunek). Wykaż, że odległość punktu 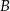 od prostej
od prostej 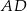 jest dwa razy większa od odległości punktu
jest dwa razy większa od odległości punktu 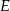 od prostej
od prostej 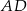 .
.
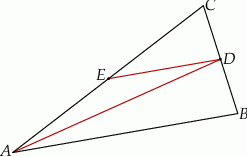
W trójkącie 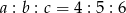 . Wykaż, że w tym trójkącie
. Wykaż, że w tym trójkącie 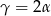 .
.
W trójkącie 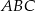 wysokość
wysokość 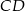 dzieli bok
dzieli bok 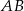 na odcinki
na odcinki 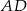 i
i 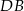 (rysunek), przy czym
(rysunek), przy czym 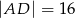 i
i 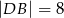 . Wykaż, że symetralna boku
. Wykaż, że symetralna boku 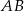 dzieli bok
dzieli bok 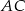 w stosunku 3:1.
w stosunku 3:1.
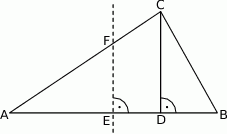
W trójkącie 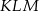 wysokość
wysokość 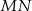 dzieli bok
dzieli bok 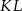 na odcinki
na odcinki 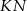 i
i 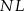 (rysunek), przy czym
(rysunek), przy czym 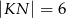 i
i 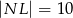 . Wykaż, że symetralna boku
. Wykaż, że symetralna boku 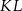 dzieli bok
dzieli bok 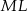 w stosunku 1:4.
w stosunku 1:4.
Dany jest trójkąt 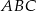 , w którym
, w którym 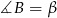 , a kąt zewnętrzny przy wierzchołku
, a kąt zewnętrzny przy wierzchołku 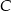 ma miarę
ma miarę  .
.
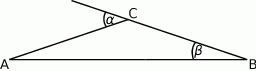
Wykaż, że jeśli 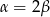 , to trójkąt
, to trójkąt 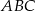 jest równoramienny.
jest równoramienny.
Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek 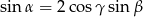 to trójkąt ten jest równoramienny.
to trójkąt ten jest równoramienny.
W trójkącie ostrokątnym 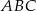 bok
bok 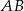 ma długość
ma długość  , długość boku
, długość boku 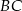 jest równa
jest równa  oraz
oraz 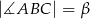 . Dwusieczna kąta
. Dwusieczna kąta 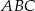 przecina bok
przecina bok 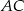 trójkąta w punkcie
trójkąta w punkcie 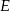 . Wykaż, że długość odcinka
. Wykaż, że długość odcinka 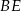 jest równa
jest równa 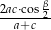 .
.
Na bokach 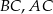 i
i 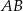 trójkąta
trójkąta 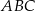 wybrano odpowiednio punkty
wybrano odpowiednio punkty 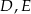 i
i 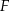 . Wykaż, że jeżeli okręgi opisane na trójkątach
. Wykaż, że jeżeli okręgi opisane na trójkątach 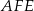 i
i 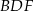 są styczne, to punkt
są styczne, to punkt 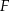 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 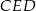 .
.
Suma długości wszystkich wysokości trójkąta 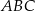 jest 9 razy większa od promienia okręgu wpisanego w ten trójkąt. Udowodnij, że trójkąt
jest 9 razy większa od promienia okręgu wpisanego w ten trójkąt. Udowodnij, że trójkąt 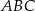 jest równoboczny.
jest równoboczny.
Uzasadnij, że jeżeli dwie dwusieczne trójkąta przecinają się pod kątem 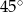 to trójkąt jest prostokątny.
to trójkąt jest prostokątny.
Punkt 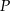 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 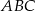 oraz
oraz 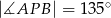 . Wykaż, że trójkąt
. Wykaż, że trójkąt 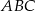 jest prostokątny.
jest prostokątny.
W trójkącie 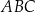 kąt
kąt 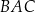 jest dwa razy większy od kąta
jest dwa razy większy od kąta 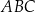 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość 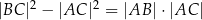 .
.
Dany jest trójkąt 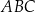 , który nie jest równoramienny. W tym trójkącie miara kąta
, który nie jest równoramienny. W tym trójkącie miara kąta 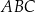 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 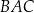 . Wykaż, że długości boków tego trójkąta spełniają warunek
. Wykaż, że długości boków tego trójkąta spełniają warunek
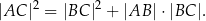
Dany jest trójkąt 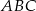 , w którym
, w którym 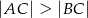 . Na bokach
. Na bokach 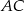 i
i 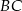 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 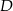 i
i 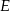 , że
, że 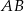 i
i 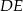 przecinają się w punkcie
przecinają się w punkcie 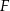 (zobacz rysunek). Wykaż, że jeżeli
(zobacz rysunek). Wykaż, że jeżeli 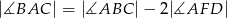 , to
, to 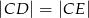 .
.
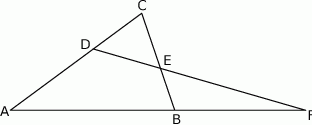
Odcinki 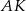 i
i 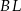 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 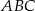 , a punkt
, a punkt 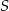 punktem ich przecięcia. Wykaż, że podobne są trójkąty:
punktem ich przecięcia. Wykaż, że podobne są trójkąty:
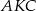 i
i 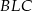 ;
; 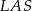 i
i 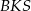 ;
; 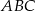 i
i 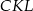 .
.Odcinki 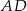 i
i 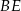 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 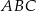 , a punkt
, a punkt 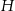 jest punktem ich przecięcia. Uzasadnij, że punkty
jest punktem ich przecięcia. Uzasadnij, że punkty 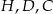 i
i 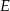 leżą na jednym okręgu.
leżą na jednym okręgu.
