Przez środek  okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt  poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku  , która przecina boki
, która przecina boki 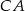 i
i 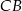 odpowiednio w punktach
odpowiednio w punktach 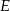 i
i 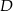 .
.
Wykaż, że 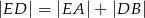 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Przez środek 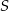 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 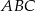 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 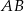 , która przecina boki
, która przecina boki 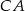 i
i 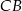 odpowiednio w punktach
odpowiednio w punktach 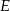 i
i 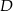 .
.
Wykaż, że 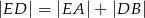 .
.

W trójkącie ostrokątnym 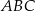 bok
bok 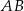 ma długość
ma długość  , długość boku
, długość boku 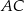 jest równa
jest równa 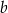 oraz
oraz 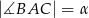 . Dwusieczna kąta
. Dwusieczna kąta 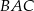 przecina bok
przecina bok 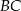 trójkąta w punkcie
trójkąta w punkcie 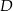 i odcinek
i odcinek 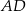 ma długość
ma długość 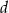 . Wykaż, że
. Wykaż, że
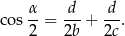
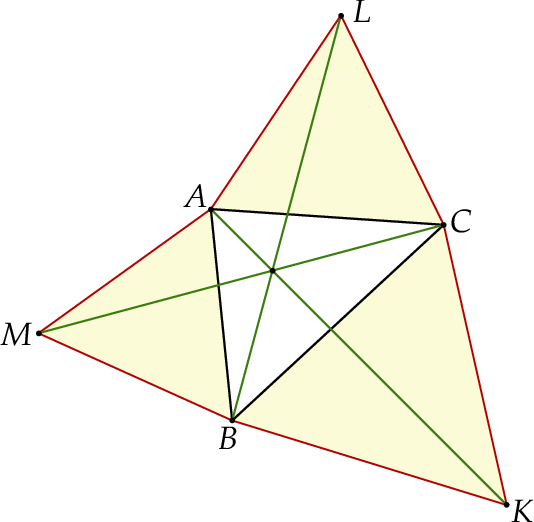
W trójkącie 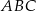 poprowadzono odcinki
poprowadzono odcinki 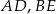 i
i 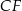 w ten sposób, że punkty
w ten sposób, że punkty 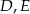 i
i 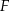 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 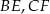 i
i 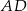 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 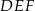 jest siedem razy mniejsze od pola trójkąta
jest siedem razy mniejsze od pola trójkąta 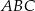 .
.
Na bokach trójkąta 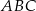 zbudowano kwadraty
zbudowano kwadraty 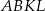 ,
, 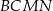 i
i 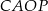 (zobacz rysunek).
(zobacz rysunek).
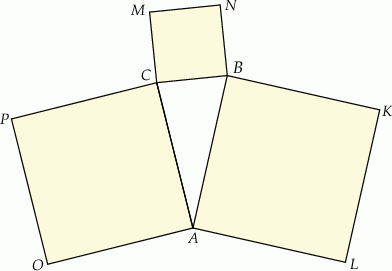
Kąty 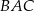 i
i 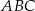 są ostre oraz suma ich tangensów jest równa
są ostre oraz suma ich tangensów jest równa  . Wykaż, że jeżeli pole kwadratu
. Wykaż, że jeżeli pole kwadratu 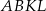 jest pięć razy większe od pola trójkąta
jest pięć razy większe od pola trójkąta 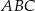 , to suma pól kwadratów
, to suma pól kwadratów 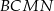 i
i 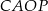 też jest pięć razy większa od pola trójkąta
też jest pięć razy większa od pola trójkąta 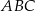 .
.
Wykaż, że istnieją dokładnie dwie liczby naturalne  takie, że trójkąt o bokach
takie, że trójkąt o bokach 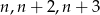 jest rozwartokątny.
jest rozwartokątny.
Każdy kąt trójkąta 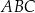 ma miarę mniejszą niż
ma miarę mniejszą niż 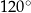 . Na bokach tego trójkąta zbudowano trójkąty równoboczne
. Na bokach tego trójkąta zbudowano trójkąty równoboczne 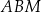 ,
, 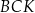 i
i 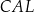 (zobacz rysunek).
(zobacz rysunek).
Wykaż, że  .
.
Wykaż, że proste 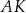 ,
, 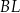 i
i 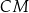 przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
Wykaż, że jeżeli  i
i 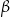 są kątami trójkąta oraz
są kątami trójkąta oraz 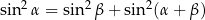 to trójkąt ten jest prostokątny.
to trójkąt ten jest prostokątny.
Dany jest trójkąt 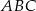 , w którym
, w którym 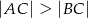 . Na bokach
. Na bokach 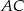 i
i 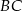 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 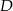 i
i 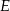 , że zachodzi równość
, że zachodzi równość 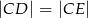 . Proste
. Proste 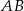 i
i 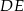 przecinają się w punkcie
przecinają się w punkcie  (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 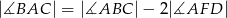 .
.
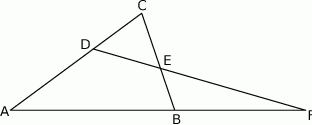
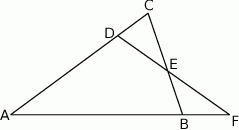
Dany jest trójkąt 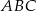 , w którym
, w którym 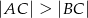 . Na bokach
. Na bokach 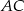 i
i 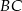 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 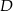 i
i 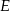 , że zachodzi równość
, że zachodzi równość 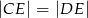 . Proste
. Proste 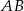 i
i 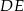 przecinają się w punkcie
przecinają się w punkcie 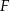 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 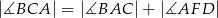 .
.
Wykaż, że jeśli 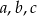 są długościami boków trójkąta ostrokątnego takimi, że
są długościami boków trójkąta ostrokątnego takimi, że 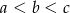 oraz
oraz 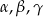 są miarami kątów tego trójkąta leżącymi odpowiednio na przeciwko boków
są miarami kątów tego trójkąta leżącymi odpowiednio na przeciwko boków 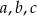 , to
, to 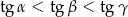 .
.
W trójkącie 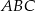 połączono środki boków i otrzymano trójkąt
połączono środki boków i otrzymano trójkąt 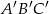 . Uzasadnij, że trójkąty
. Uzasadnij, że trójkąty 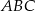 i
i 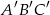 są podobne.
są podobne.
Punkty 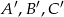 są środkami odpowiednio boków
są środkami odpowiednio boków 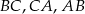 trójkąta
trójkąta 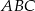 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 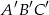 jest przystający do trójkąta
jest przystający do trójkąta 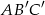 .
.
Trójkąt 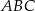 jest ostrokątny oraz
jest ostrokątny oraz 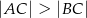 . Dwusieczna
. Dwusieczna 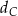 kąta
kąta 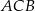 przecina bok
przecina bok 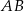 w punkcie
w punkcie 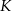 . Punkt
. Punkt 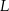 jest obrazem punktu
jest obrazem punktu 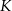 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 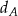 kąta
kąta 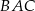 , punkt
, punkt 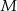 jest obrazem punktu
jest obrazem punktu 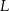 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 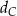 kąta
kąta 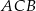 , a punkt
, a punkt 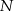 jest obrazem punktu
jest obrazem punktu 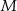 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 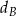 kąta
kąta 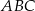 (zobacz rysunek).
(zobacz rysunek).
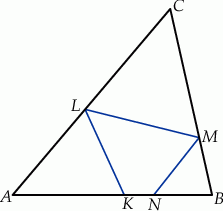
Udowodnij, że na czworokącie 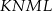 można opisać okrąg.
można opisać okrąg.
Na bokach 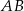 ,
, 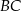 i
i 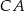 trójkąta
trójkąta 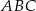 wybrano odpowiednio punkty
wybrano odpowiednio punkty 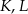 i
i 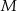 w ten sposób, że
w ten sposób, że 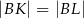 i
i 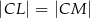 . Okrąg opisany na trójkącie
. Okrąg opisany na trójkącie 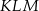 przecina bok
przecina bok 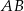 tego trójkąta w punkcie
tego trójkąta w punkcie 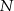 takim, że
takim, że 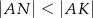 (zobacz rysunek).
(zobacz rysunek).
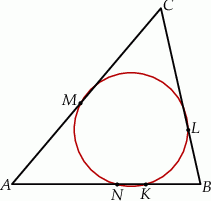
Udowodnij, że 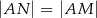 .
.
W trójkącie 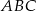 bok
bok 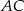 ma długość
ma długość 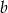 ,
, 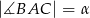 oraz
oraz  . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta  jest równe
jest równe
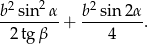
Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek 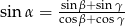 to trójkąt ten jest prostokątny.
to trójkąt ten jest prostokątny.
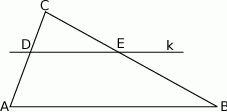
Prosta 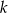 równoległa do boku
równoległa do boku 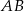 trójkąta
trójkąta 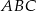 przecina boki
przecina boki 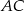 oraz
oraz 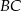 odpowiednio w punktach
odpowiednio w punktach 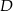 i
i 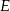 (zobacz rysunek). Wiadomo, że pole trójkąta
(zobacz rysunek). Wiadomo, że pole trójkąta 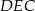 wynosi
wynosi 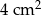 , zaś pole trapezu
, zaś pole trapezu  jest równe
jest równe 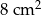 . Wykaż, że
. Wykaż, że 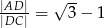 .
.
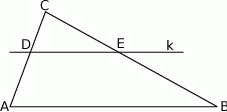
Prosta  równoległa do boku
równoległa do boku  trójkąta
trójkąta  przecina boki
przecina boki 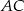 oraz
oraz 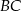 odpowiednio w punktach
odpowiednio w punktach 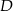 i
i 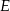 (zobacz rysunek). Wiadomo, że pole trójkąta
(zobacz rysunek). Wiadomo, że pole trójkąta 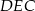 wynosi
wynosi 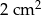 , zaś pole trapezu
, zaś pole trapezu 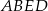 jest równe
jest równe 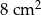 . Wykaż, że
. Wykaż, że 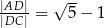 .
.
Udowodnij, że jeżeli w trójkącie dwa kąty nie są równe, to naprzeciw większego z nich leży dłuższy bok.
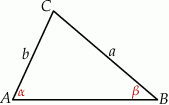
Wykaż, że pole trójkąta o bokach 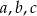 i promieniu
i promieniu 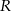 okręgu opisanego na nim jest równe
okręgu opisanego na nim jest równe 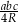 .
.
Wykaż, że pole trójkąta 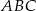 jest równe
jest równe 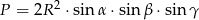 , gdzie
, gdzie 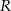 jest promieniem okręgu opisanego na tym trójkącie, a
jest promieniem okręgu opisanego na tym trójkącie, a 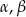 i
i 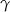 są miarami kątów wewnętrznych tego trójkąta.
są miarami kątów wewnętrznych tego trójkąta.
Dany jest trójkąt 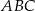 . Punkt
. Punkt  jest środkiem boku
jest środkiem boku 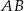 tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów
tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów 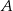 i
i 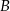 od prostej
od prostej 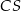 są równe.
są równe.
Na boku  trójkąta
trójkąta  wybrano punkt
wybrano punkt  w ten sposób, że odległości punktów
w ten sposób, że odległości punktów 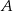 i
i 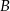 od prostej
od prostej 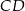 są równe (zobacz rysunek). Wykaż, że trójkąty
są równe (zobacz rysunek). Wykaż, że trójkąty 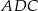 i
i 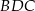 mają równe pola.
mają równe pola.
Odcinki  i
i  są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 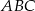 , a punkt
, a punkt 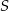 jest punktem ich przecięcia. Uzasadnij, że:
jest punktem ich przecięcia. Uzasadnij, że:
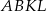 można opisać okrąg;
można opisać okrąg; 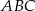 i
i 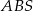 mają promienie równej długości.
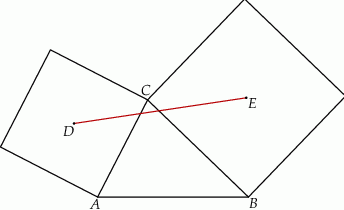
mają promienie równej długości.Pole trójkąta 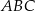 jest równe
jest równe 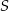 , a długości jego boków
, a długości jego boków 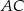 i
i 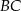 są odpowiednio równe
są odpowiednio równe 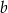 i
i  . Na bokach
. Na bokach 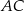 i
i 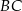 zbudowano kwadraty o środkach odpowiednio
zbudowano kwadraty o środkach odpowiednio 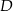 i
i 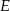 .
.
Wykaż, że
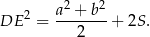
Wykaż, że jeżeli w trójkącie 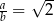 to
to 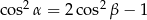 .
.