Na bokach 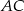 i
i 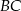 trójkąta
trójkąta 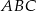 obrano punkty
obrano punkty 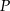 i
i 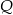 takie, że
takie, że 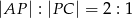 oraz
oraz 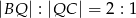 . Odcinki
. Odcinki 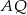 i
i 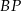 przecinają się w punkcie
przecinają się w punkcie 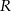 . Wykaż, że pole czworokąta
. Wykaż, że pole czworokąta 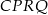 jest równe polu trójkąta
jest równe polu trójkąta 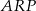 .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Udowodnij...
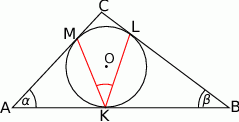
W trójkąt 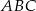 , w którym
, w którym 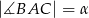 oraz
oraz 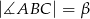 , wpisano okrąg. Punkty
, wpisano okrąg. Punkty 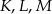 są punktami styczności okręgu odpowiednio z bokami
są punktami styczności okręgu odpowiednio z bokami 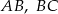 i
i 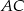 . Wykaż, że
. Wykaż, że 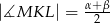 .
.
Proste zawierające wysokości trójkąta ostrokątnego 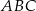 przecinają boki
przecinają boki 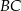 ,
, 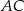 i
i 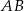 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 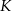 ,
, 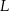 i
i 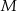 . Wykaż, że jeżeli trójkąt
. Wykaż, że jeżeli trójkąt 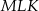 jest podobny do trójkąta
jest podobny do trójkąta 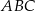 , to trójkąt
, to trójkąt 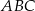 jest równoboczny.
jest równoboczny.
Wysokości w pewnym trójkącie 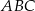 mają długości:
mają długości: 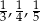 . Wykaż, że jest to trójkąt prostokątny.
. Wykaż, że jest to trójkąt prostokątny.
Dane są dwa trójkąty: 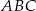 oraz
oraz 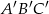 takie, że
takie, że 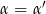 oraz
oraz 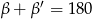 .
.
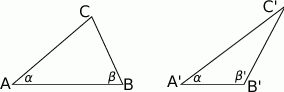
Wykaż, że:
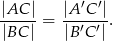
W trójkącie 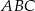 poprowadzono dwusieczne kątów przecinające boki
poprowadzono dwusieczne kątów przecinające boki 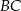 ,
, 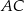 i
i 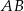 tego trójkąta w punktach – odpowiednio –
tego trójkąta w punktach – odpowiednio – 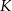 ,
, 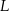 oraz
oraz 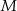 . Punkt
. Punkt 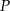 jest punktem przecięcia tych dwusiecznych. Na czworokątach
jest punktem przecięcia tych dwusiecznych. Na czworokątach 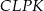 oraz
oraz 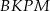 można opisać okrąg. Udowodnij, że trójkąt
można opisać okrąg. Udowodnij, że trójkąt 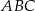 jest równoboczny.
jest równoboczny.
Wykaż, że jeżeli 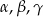 są kątami wewnętrznymi trójkąta i
są kątami wewnętrznymi trójkąta i 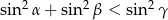 , to
, to 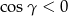 .
.
Wykaż, że jeżeli 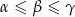 są kątami wewnętrznymi trójkąta rozwartokątnego, to
są kątami wewnętrznymi trójkąta rozwartokątnego, to
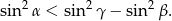
W trójkącie 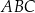 dwusieczna kąta
dwusieczna kąta 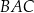 przecina bok
przecina bok 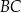 trójkąta w punkcie
trójkąta w punkcie 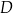 . Wykaż, że
. Wykaż, że
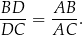
Trójkąty 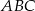 i
i 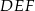 wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
W trójkącie 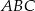 miara kąta
miara kąta 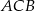 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 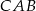 . Dwusieczna kąta
. Dwusieczna kąta 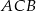 dzieli trójkąt
dzieli trójkąt 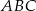 na dwa trójkąty. Uzasadnij, że jeden z otrzymanych trójkątów jest podobny do trójkąta
na dwa trójkąty. Uzasadnij, że jeden z otrzymanych trójkątów jest podobny do trójkąta 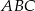 .
.
Miary kątów trójkąta 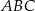 są równe
są równe 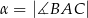 ,
, 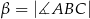 i
i 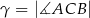 . Punkt
. Punkt 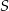 jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki
jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki 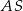 i
i 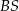 przecinają boki
przecinają boki 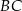 i
i 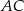 tego trójkąta w punktach odpowiednio
tego trójkąta w punktach odpowiednio 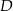 i
i 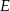 (zobacz rysunek).
(zobacz rysunek).
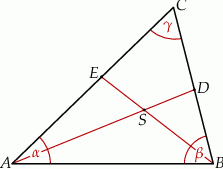
Wykaż, że jeżeli 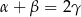 , to na czworokącie
, to na czworokącie 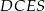 można opisać okrąg.
można opisać okrąg.
Dany jest trójkąt 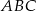 , w którym
, w którym 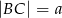 . Z wierzchołka
. Z wierzchołka 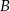 poprowadzono środkową
poprowadzono środkową 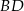 do boku
do boku 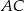 . Punkt
. Punkt 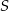 jest środkiem odcinka
jest środkiem odcinka 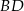 . Przez punkty
. Przez punkty 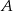 i
i 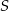 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 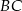 w punkcie
w punkcie 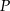 . Wykaż, że długość odcinka
. Wykaż, że długość odcinka 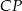 jest równa
jest równa 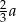 .
.
Dany jest trójkąt 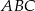 oraz punkt
oraz punkt 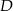 na jego boku
na jego boku 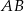 taki, że
taki, że 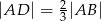 . Z wierzchołka
. Z wierzchołka 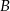 poprowadzono środkową
poprowadzono środkową 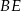 do boku
do boku 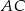 . Punkt
. Punkt 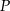 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 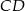 i
i 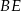 . Wykaż, że punkt
. Wykaż, że punkt 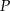 jest środkiem odcinka
jest środkiem odcinka 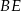 .
.
Wykaż, że jeżeli trójkąt nie jest rozwartokątny, oraz miara  jednego z jego kątów spełnia warunek
jednego z jego kątów spełnia warunek 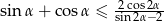 to trójkąt ten jest prostokątny.
to trójkąt ten jest prostokątny.
Wierzchołek 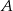 trójkąta ostrokątnego
trójkąta ostrokątnego 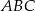 połączono odcinkiem ze środkiem
połączono odcinkiem ze środkiem 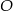 okręgu opisanego. Z wierzchołka
okręgu opisanego. Z wierzchołka 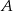 poprowadzono wysokość
poprowadzono wysokość 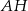 . Wykaż, że
. Wykaż, że 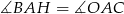 .
.
Trójkąt 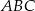 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 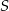 . Kąty wewnętrzne
. Kąty wewnętrzne 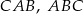 i
i 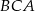 tego trójkąta są równe, odpowiednio,
tego trójkąta są równe, odpowiednio, 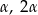 i
i 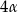 . Wykaż, że trójkąt
. Wykaż, że trójkąt 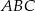 jest rozwartokątny, i udowodnij, że miary wypukłych kątów środkowych
jest rozwartokątny, i udowodnij, że miary wypukłych kątów środkowych 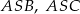 i
i 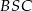 tworzą w podanej kolejności ciąg arytmetyczny.
tworzą w podanej kolejności ciąg arytmetyczny.
W trójkącie 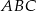 przedłużono bok
przedłużono bok 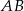 poza wierzchołek
poza wierzchołek 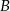 i odłożono odcinek
i odłożono odcinek 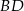 taki, że
taki, że 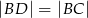 . Następnie połączono punkty
. Następnie połączono punkty 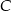 i
i 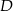 (rysunek). Wykaż, że
(rysunek). Wykaż, że 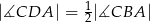 .
.
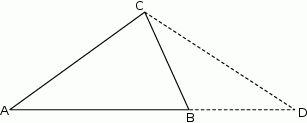
W trójkącie 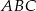 przedłużono bok
przedłużono bok 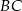 poza wierzchołek
poza wierzchołek 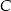 i odłożono odcinek
i odłożono odcinek 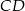 taki, że
taki, że 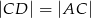 . Następnie połączono punkty
. Następnie połączono punkty 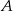 i
i 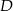 (rysunek). Wykaż, że
(rysunek). Wykaż, że 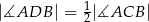 .
.
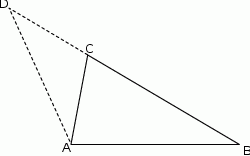
Uzasadnij wzór na pole trójkąta 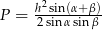 , gdzie
, gdzie  i
i 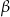 są miarami kątów trójkąta przyległych do boku, na który opuszczono wysokość
są miarami kątów trójkąta przyległych do boku, na który opuszczono wysokość 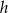 .
.
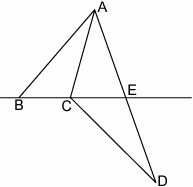
Wiedząc, że punkt 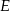 jest środkiem odcinka
jest środkiem odcinka 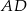 , a punkt
, a punkt 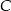 jest środkiem odcinka
jest środkiem odcinka 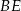 oraz
oraz 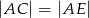 , wykaż, że
, wykaż, że 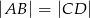 .
.
W trójkącie 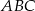 na boku
na boku 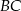 zaznaczono punkt
zaznaczono punkt 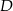 , na boku
, na boku 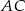 zaznaczono punkt
zaznaczono punkt 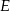 , na boku
, na boku 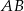 punkt
punkt 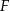 . Poprowadzono okręgi
. Poprowadzono okręgi 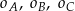 , w ten sposób, że do okręgu
, w ten sposób, że do okręgu 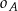 należą punkty
należą punkty 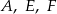 , do
, do 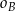 – punkty
– punkty 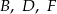 , a do
, a do 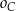 – punkty
– punkty 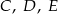 . Wykaż, że te trzy okręgi przecinają się w jednym punkcie.
. Wykaż, że te trzy okręgi przecinają się w jednym punkcie.
Okrąg 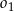 przechodzi przez wierzchołek
przechodzi przez wierzchołek 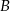 trójkąta
trójkąta 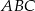 i przecina jego boki
i przecina jego boki 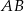 i
i 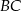 odpowiednio w punktach
odpowiednio w punktach 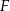 i
i 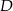 . Okrąg
. Okrąg 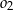 przechodzi przez wierzchołek
przechodzi przez wierzchołek 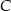 , przecina okrąg
, przecina okrąg 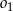 w punkcie
w punkcie 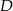 oraz w punkcie
oraz w punkcie 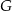 leżącym wewnątrz trójkąta
leżącym wewnątrz trójkąta 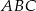 . Ponadto okrąg
. Ponadto okrąg 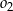 przecina bok
przecina bok 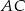 trójkąta w punkcie
trójkąta w punkcie 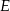 .
.
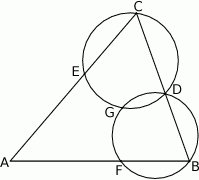
Udowodnij, że punkt 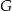 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 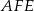 .
.
W trójkącie 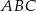 na boku
na boku 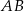 wybrano takie punkty
wybrano takie punkty 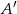 i
i 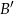 , że
, że
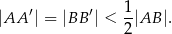
Przez punkty 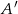 i
i 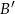 poprowadzono proste równoległe do boków odpowiednio
poprowadzono proste równoległe do boków odpowiednio 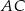 i
i 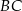 . Proste te przecięły się w punkcie
. Proste te przecięły się w punkcie 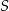 . Wykaż, że odcinek
. Wykaż, że odcinek 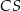 jest zawarty w środkowej trójkąta
jest zawarty w środkowej trójkąta 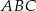 .
.

