Punkty 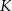 i
i 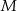 oraz
oraz 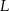 i
i 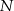 dzielą odpowiednio boki
dzielą odpowiednio boki 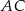 i
i 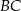 trójkąta
trójkąta 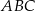 w stosunku
w stosunku 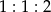 (zobacz rysunek). Odcinki
(zobacz rysunek). Odcinki 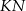 i
i 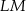 przecinają się w punkcie
przecinają się w punkcie 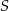 .
.
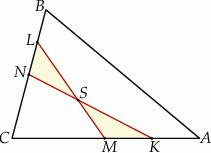
Uzasadnij, że pola trójkątów 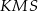 i
i 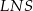 są równe.
są równe.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkty 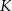 i
i 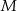 oraz
oraz 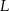 i
i 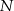 dzielą odpowiednio boki
dzielą odpowiednio boki 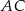 i
i 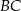 trójkąta
trójkąta 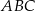 w stosunku
w stosunku 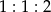 (zobacz rysunek). Odcinki
(zobacz rysunek). Odcinki 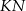 i
i 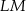 przecinają się w punkcie
przecinają się w punkcie 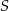 .
.

Uzasadnij, że pola trójkątów 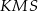 i
i 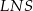 są równe.
są równe.
Wykaż, że jeżeli 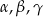 są kątami wewnętrznymi trójkąta i
są kątami wewnętrznymi trójkąta i 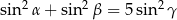 , to
, to 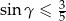 .
.
W trójkącie 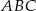 poprowadzono dwusieczne kątów
poprowadzono dwusieczne kątów 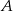 i
i 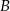 . Dwusieczne te przecinają się w punkcie
. Dwusieczne te przecinają się w punkcie 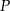 . Uzasadnij, że kąt
. Uzasadnij, że kąt 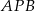 jest rozwarty.
jest rozwarty.
W trójkącie ostrokątnym 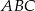 proste
proste 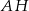 i
i 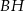 zawierają wysokości poprowadzone z wierzchołków
zawierają wysokości poprowadzone z wierzchołków 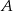 i
i 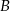 . Uzasadnij, że kąt
. Uzasadnij, że kąt 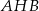 jest rozwarty.
jest rozwarty.
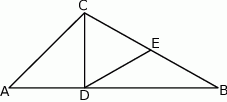
Dany jest trójkąt 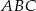 . Odcinek
. Odcinek 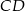 jest wysokością tego trójkąta, punkt
jest wysokością tego trójkąta, punkt 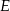 jest środkiem boku
jest środkiem boku 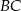 (tak jak na rysunku) i
(tak jak na rysunku) i 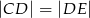 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 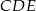 jest równoboczny.
jest równoboczny.
Wykaż, że jeżeli kąty trójkąta: 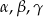 spełniają równanie
spełniają równanie 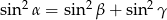 to trójkąt jest prostokątny.
to trójkąt jest prostokątny.
Wykaż, że jeżeli środkowa trójkąta jest dwa razy krótsza od boku, do którego jest poprowadzona, to trójkąt ten jest prostokątny.
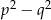 ,
, 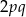 i
i 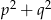 , gdzie
, gdzie 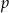 i
i 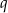 są liczbami dodatnimi takimi, że
są liczbami dodatnimi takimi, że 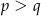 , to trójkąt ten jest prostokątny.
, to trójkąt ten jest prostokątny. 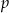 i
i 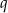 , dla których najkrótszy bok otrzymanego trójkąta ma długość 13.
, dla których najkrótszy bok otrzymanego trójkąta ma długość 13.Udowodnij, że jeżeli środek okręgu opisanego na trójkącie leży na jednym z jego boków, to trójkąt ten jest prostokątny.
Wykaż, że jeżeli długości 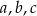 boków trójkąta spełniają równość
boków trójkąta spełniają równość
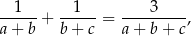
to promień okręgu opisanego na tym trójkącie jest równy 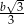 .
.
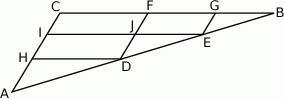
Odcinki 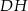 i
i 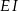 są równoległe do boku
są równoległe do boku 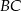 trójkąta
trójkąta 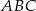 , a odcinki
, a odcinki 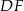 i
i 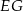 są równoległe do boku
są równoległe do boku 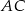 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 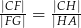 , to
, to 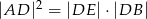 .
.
W trójkącie 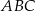 poprowadzono dwusieczne kątów przecinające boki
poprowadzono dwusieczne kątów przecinające boki 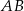 i
i 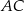 tego trójkąta w punktach – odpowiednio –
tego trójkąta w punktach – odpowiednio – 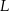 i
i 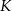 . Punkt
. Punkt 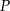 jest punktem przecięcia tych dwusiecznych. Długości boków trójkąta
jest punktem przecięcia tych dwusiecznych. Długości boków trójkąta 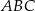 spełniają warunki:
spełniają warunki: 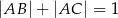 oraz
oraz
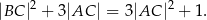
Udowodnij, że punkt 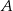 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 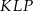 .
.
W trójkącie 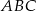 dwusieczna kąta
dwusieczna kąta 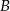 przecina bok
przecina bok 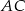 w punkcie
w punkcie 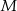 . Przez punkt
. Przez punkt 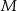 prowadzimy prostą równoległą do
prowadzimy prostą równoległą do 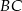 , przecinającą bok
, przecinającą bok 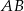 w punkcie
w punkcie 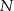 (rys.). Udowodnij, że
(rys.). Udowodnij, że 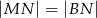 .
.
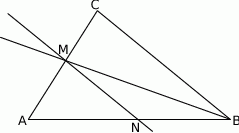
W trójkącie 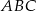 dwusieczna kąta
dwusieczna kąta 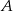 przecina bok
przecina bok 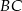 w punkcie
w punkcie 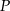 . Przez punkt
. Przez punkt 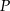 prowadzimy prostą równoległą do
prowadzimy prostą równoległą do 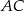 , przecinającą bok
, przecinającą bok 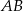 w punkcie
w punkcie 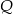 (rys.). Udowodnij, że
(rys.). Udowodnij, że 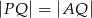 .
.
Wykaż, że jeżeli kąty 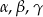 trójkąta
trójkąta 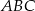 spełniają warunek
spełniają warunek 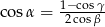 to trójkąt jest równoramienny.
to trójkąt jest równoramienny.
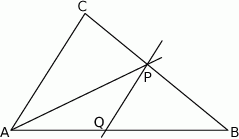
Odcinek 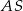 jest środkową trójkąta
jest środkową trójkąta 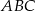 . Udowodnij, że
. Udowodnij, że 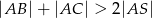 .
.
Okrąg wpisany w trójkąt 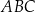 jest styczny do boków
jest styczny do boków 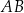 i
i 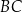 w punktach
w punktach 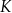 i
i 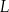 odpowiednio. Na bokach
odpowiednio. Na bokach 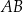 i
i 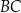 tego trójkąta wybrano punkty
tego trójkąta wybrano punkty 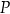 i
i 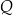 w ten sposób, że odcinek
w ten sposób, że odcinek 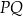 jest styczny do okręgu wpisanego w trójkąt
jest styczny do okręgu wpisanego w trójkąt 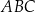 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że jeżeli 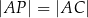 ,
, 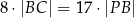 i
i 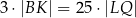 , to trójkąt
, to trójkąt 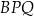 jest rozwartokątny.
jest rozwartokątny.
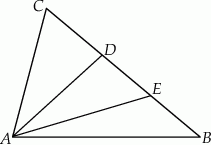
Punkty 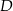 i
i 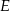 dzielą bok
dzielą bok 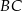 trójkąta
trójkąta 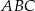 na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta
na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta 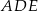 jest trzy razy mniejsze od pola trójkąta
jest trzy razy mniejsze od pola trójkąta  .
.
Wykaż, że suma odległości dowolnego punktu wewnętrznego trójkąta od jego wierzchołków jest większa od połowy obwodu trójkąta.
Wykaż, że odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i ma długość równą połowie tego boku.
W trójkącie ostrokątnym  prawdziwa jest równość
prawdziwa jest równość 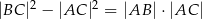 . Wykaż, że kąt
. Wykaż, że kąt 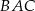 jest dwa razy większy od kąta
jest dwa razy większy od kąta 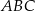 .
.
Wykaż, że jeżeli w trójkącie dwusieczna pokrywa się ze środkową, to trójkąt ten jest równoramienny.
