W trójkącie 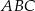 punkt
punkt 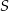 jest środkiem okręgu wpisanego, a punkty
jest środkiem okręgu wpisanego, a punkty 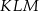 są punktami styczności okręgu wpisanego w trójkąt z bokami
są punktami styczności okręgu wpisanego w trójkąt z bokami 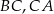 i
i 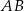 odpowiednio.
odpowiednio.
- Uzasadnij, że na czworokącie
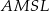 można opisać okrąg.
można opisać okrąg. - Wiedząc, że
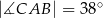 oraz
oraz 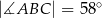 oblicz miary kątów trójkąta
oblicz miary kątów trójkąta 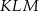 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie 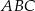 punkt
punkt 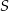 jest środkiem okręgu wpisanego, a punkty
jest środkiem okręgu wpisanego, a punkty 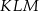 są punktami styczności okręgu wpisanego w trójkąt z bokami
są punktami styczności okręgu wpisanego w trójkąt z bokami 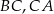 i
i 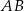 odpowiednio.
odpowiednio.
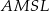 można opisać okrąg.
można opisać okrąg. 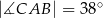 oraz
oraz 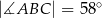 oblicz miary kątów trójkąta
oblicz miary kątów trójkąta 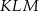 .
.Wykaż, że jeżeli 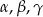 są kątami trójkąta, to
są kątami trójkąta, to
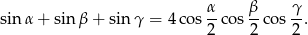
W trójkącie 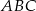 środkowa
środkowa 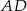 jest prostopadła do boku
jest prostopadła do boku 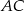 . Kąt
. Kąt 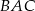 ma miarę
ma miarę 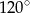 . Wykaż, że
. Wykaż, że 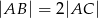 .
.
Środkowa 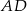 trójkąta
trójkąta 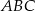 ma długość równą połowie długości boku
ma długość równą połowie długości boku 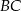 oraz
oraz 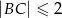 . Wykaż, że
. Wykaż, że 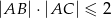 .
.
Na bokach 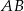 ,
, 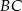 i
i 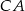 trójkąta
trójkąta 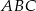 wybrano odpowiednio punkty
wybrano odpowiednio punkty 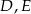 i
i 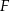 . Wykaż, że okręgi opisane na trójkątach
. Wykaż, że okręgi opisane na trójkątach 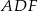 ,
, 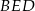 i
i 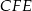 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
W trójkącie 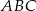 środkowe
środkowe 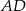 i
i 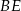 są prostopadłe. Wykaż, że
są prostopadłe. Wykaż, że 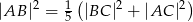 .
.
Wykaż, że jeśli 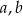 są długościami boków trójkąta ostrokątnego takimi, że
są długościami boków trójkąta ostrokątnego takimi, że 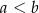 oraz
oraz 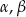 są miarami kątów tego trójkąta leżącymi odpowiednio naprzeciwko boków
są miarami kątów tego trójkąta leżącymi odpowiednio naprzeciwko boków 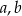 , to
, to 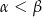 .
.
W trójkącie 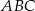 punkt
punkt 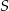 jest środkiem okręgu wpisanego, a punkty
jest środkiem okręgu wpisanego, a punkty 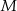 i
i 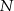 są punktami styczności tego okręgu z bokami
są punktami styczności tego okręgu z bokami 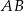 i
i 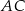 odpowiednio. Wykaż, że punkt
odpowiednio. Wykaż, że punkt 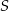 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 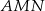 .
.
Wykaż, że jeżeli 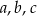 są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach
są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach 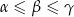 to
to 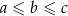 .
.
Każdy kąt trójkąta 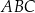 ma miarę mniejszą niż
ma miarę mniejszą niż 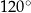 . Udowodnij, że wewnątrz trójkąta
. Udowodnij, że wewnątrz trójkąta 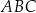 istnieje punkt
istnieje punkt 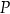 taki, że
taki, że
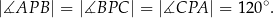
Dwa boki trójkąta ostrokątnego wpisanego w okrąg o promieniu 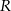 mają długości
mają długości 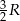 i
i 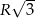 . Wykaż, że długość trzeciego boku wynosi
. Wykaż, że długość trzeciego boku wynosi 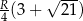 .
.
Trzy cięciwy okręgu o promieniu  tworzą trójkąt wpisany w ten okrąg. Dwie najkrótsze z tych cięciw mają długości
tworzą trójkąt wpisany w ten okrąg. Dwie najkrótsze z tych cięciw mają długości 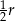 i
i 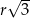 . Wykaż, że trzecia cięciwa ma długość
. Wykaż, że trzecia cięciwa ma długość 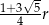 .
.
Wykaż, że jeżeli 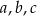 są długościami boków trójkąta to
są długościami boków trójkąta to 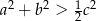 .
.
Na bokach trójkąta zbudowano kwadraty o polach 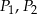 i
i  (zobacz rysunek)
(zobacz rysunek)
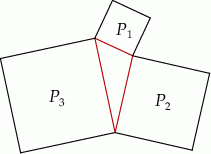
Wykaż, że 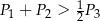 .
.
Styczna w punkcie 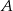 do okręgu opisanego na trójkącie
do okręgu opisanego na trójkącie 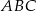 przecina prostą
przecina prostą 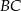 w punkcie
w punkcie 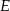 . Niech
. Niech 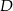 będzie punktem przecięcia dwusiecznej kąta
będzie punktem przecięcia dwusiecznej kąta 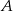 z prostą
z prostą 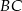 . Udowodnić, że
. Udowodnić, że 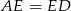 .
.
W trójkącie 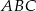 , o bokach długości
, o bokach długości 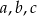 , połączono odcinkiem wierzchołek
, połączono odcinkiem wierzchołek 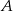 z punktem
z punktem 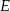 na boku
na boku 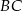 takim, że
takim, że 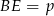 i
i 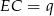 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 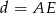 , to
, to 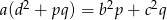 (twierdzenie Stewarta).
(twierdzenie Stewarta).
Dany jest trójkąt 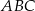 . Na boku
. Na boku 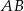 tego trójkąta obrano punkty
tego trójkąta obrano punkty 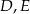 i
i 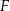 tak, że
tak, że 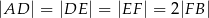 . Na bokach
. Na bokach 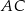 i
i 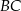 obrano – odpowiednio – punkty
obrano – odpowiednio – punkty 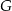 i
i 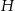 tak, że
tak, że 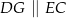 oraz
oraz 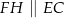 (zobacz rysunek). Wykaż, że jeżeli pole trójkąta
(zobacz rysunek). Wykaż, że jeżeli pole trójkąta 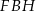 jest równe
jest równe 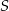 , to pole trójkąta
, to pole trójkąta 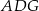 jest równe
jest równe  .
.
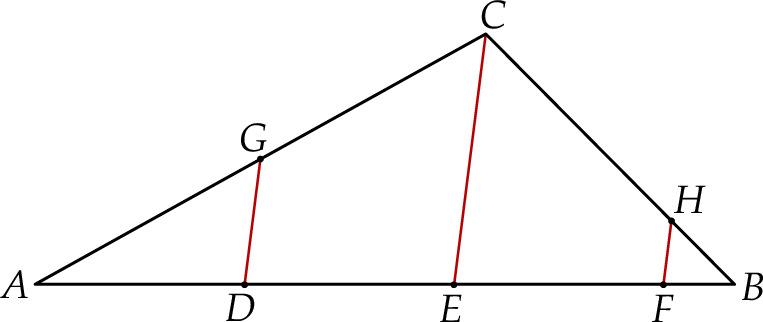
Dany jest trójkąt 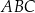 . Na boku
. Na boku 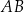 tego trójkąta obrano punkty
tego trójkąta obrano punkty 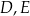 i
i 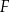 tak, że
tak, że 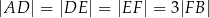 . Na bokach
. Na bokach 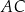 i
i 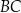 obrano – odpowiednio – punkty
obrano – odpowiednio – punkty 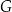 i
i 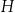 tak, że
tak, że 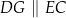 oraz
oraz 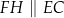 (zobacz rysunek). Wykaż, że jeżeli pole trójkąta
(zobacz rysunek). Wykaż, że jeżeli pole trójkąta 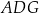 jest równe
jest równe 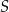 , to pole trójkąta
, to pole trójkąta 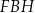 jest równe
jest równe 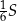 .
.
Wykaż, że jeśli  i
i 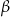 są kątami trójkąta oraz
są kątami trójkąta oraz 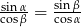 to trójkąt ten jest równoramienny lub prostokątny.
to trójkąt ten jest równoramienny lub prostokątny.
Kąty w trójkącie mają miary: 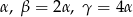 . Wykaż, że długości boków
. Wykaż, że długości boków 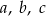 tego trójkąta spełniają równość:
tego trójkąta spełniają równość: 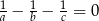 .
.
Punkty 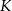 i
i 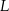 są środkami boków
są środkami boków 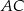 i
i 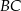 trójkąta
trójkąta 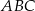 . Odcinki
. Odcinki 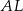 i
i 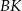 przecinają się w punkcie
przecinają się w punkcie 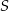 .
.
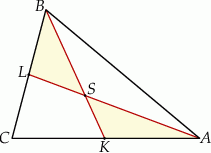
Uzasadnij, że pola trójkątów 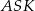 i
i 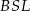 są równe.
są równe.
Punkt 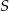 jest punktem przecięcia się wysokości trójkąta ostrokątnego
jest punktem przecięcia się wysokości trójkąta ostrokątnego 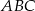 . Wykaż, że jeżeli
. Wykaż, że jeżeli 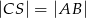 to
to 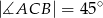 .
.
Środkowa trójkąta jest równa połowie boku, do którego została poprowadzona. Wykaż, że trójkąt ten jest prostokątny.
