Czworokąt 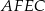 jest wpisany w okrąg i jego przekątna
jest wpisany w okrąg i jego przekątna 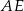 przecina okrąg opisany na trójkącie
przecina okrąg opisany na trójkącie 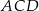 w punkcie
w punkcie 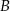 (zobacz rysunek).
(zobacz rysunek).
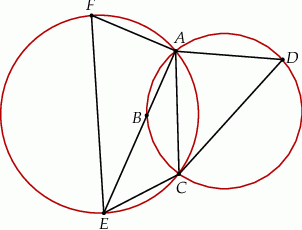
Zachodzi ponadto równość 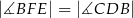 . Udowodnij, że punkty
. Udowodnij, że punkty 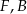 i
i 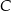 są współliniowe.
są współliniowe.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Czworokąt 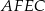 jest wpisany w okrąg i jego przekątna
jest wpisany w okrąg i jego przekątna 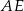 przecina okrąg opisany na trójkącie
przecina okrąg opisany na trójkącie 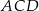 w punkcie
w punkcie 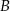 (zobacz rysunek).
(zobacz rysunek).

Zachodzi ponadto równość 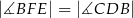 . Udowodnij, że punkty
. Udowodnij, że punkty 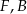 i
i 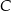 są współliniowe.
są współliniowe.
Przekątne podzieliły czworokąt na 4 trójkąty.
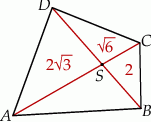
Korzystając z podanych pól trzech z tych trójkątów, wyznacz pole trójkąta 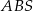 .
.
Dany jest czworokąt wypukły 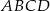 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 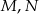 są odpowiednio środkami boków
są odpowiednio środkami boków 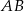 i
i 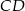 . Punkty
. Punkty 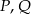 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 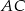 i
i 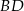 . Uzasadnij, że jeżeli odcinki
. Uzasadnij, że jeżeli odcinki 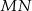 i
i 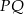 są prostopadłe, to
są prostopadłe, to 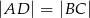 .
.
Wykaż, że jeżeli odcinki łączące środki przeciwległych boków czworokąta są prostopadłe, to przekątne tego czworokąta mają równe długości.
Wierzchołki rombu 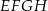 leżą na bokach trójkąta
leżą na bokach trójkąta 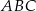 , przy czym boki
, przy czym boki 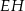 i
i 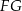 są równoległe do środkowej
są równoległe do środkowej 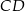 trójkąta
trójkąta 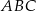 (zobacz rysunek).
(zobacz rysunek).
Oblicz długość boku rombu 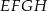 jeżeli
jeżeli 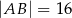 i
i 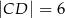 .
.
Na czworokącie wypukłym 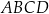 można opisać okrąg. Wiadomo, że
można opisać okrąg. Wiadomo, że 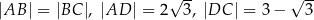 oraz przekątna
oraz przekątna 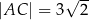 . Oblicz pole tego czworokąta.
. Oblicz pole tego czworokąta.
W okrąg o promieniu 7 wpisano czworokąt 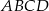 . Oblicz obwód i pole tego czworokąta, wiedząc, że
. Oblicz obwód i pole tego czworokąta, wiedząc, że 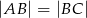 ,
, 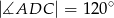 i stosunek pola trójkąta
i stosunek pola trójkąta 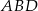 do pola trójkąta
do pola trójkąta 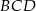 wynosi 2:1.
wynosi 2:1.
Przekątne czworokąta 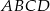 są prostopadłe.
są prostopadłe.
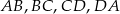 są kolejnymi wyrazami ciągu geometrycznego to czworokąt ten jest rombem.
są kolejnymi wyrazami ciągu geometrycznego to czworokąt ten jest rombem.Wykaż, że jeżeli dwusieczne dwóch sąsiednich kątów wewnętrznych czworokąta wypukłego są prostopadłe, to czworokąt ten jest trapezem.
W czworokącie wypukłym 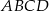 dane są:
dane są: 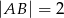 ,
, 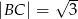 ,
, 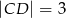 ,
, 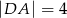 i
i 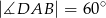 . Oblicz pole tego czworokąta.
. Oblicz pole tego czworokąta.
Czworokąt 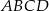 jest wpisany w okrąg oraz
jest wpisany w okrąg oraz 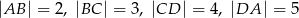 .
.
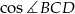 .
. 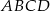 .
.Przekątne czworokąta wypukłego 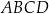 wpisanego w okrąg przecinają się w punkcie
wpisanego w okrąg przecinają się w punkcie 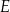 tak, że
tak, że 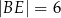 ,
, 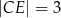 i
i 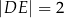 . Ponadto
. Ponadto 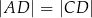 (zobacz rysunek).
(zobacz rysunek).

Oblicz długości boków czworokąta 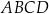 oraz promień opisanego na nim okręgu.
oraz promień opisanego na nim okręgu.
W czworokącie wypukłym 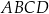 , długości boków
, długości boków 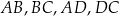 są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że dwusieczne kątów wewnętrznych tego czworokąta przecinają się w jednym punkcie.
są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że dwusieczne kątów wewnętrznych tego czworokąta przecinają się w jednym punkcie.
Dany jest czworokąt wypukły 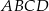 , w którym
, w którym 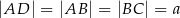 ,
, 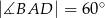 i
i 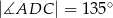 . Oblicz pole czworokąta
. Oblicz pole czworokąta 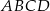 .
.
Boki 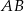 i
i 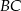 czworokąta
czworokąta 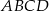 wpisanego w okrąg są równe przekątnej
wpisanego w okrąg są równe przekątnej 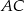 . Kąt
. Kąt 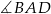 ma miarę
ma miarę 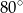 . Znajdź miary pozostałych kątów czworokąta
. Znajdź miary pozostałych kątów czworokąta 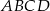 .
.
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
Czworokąt 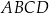 , w którym
, w którym 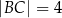 i
i 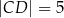 , jest opisany na okręgu. Przekątna
, jest opisany na okręgu. Przekątna 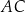 tego czworokąta tworzy z bokiem
tego czworokąta tworzy z bokiem 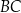 kąt o mierze
kąt o mierze 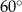 , natomiast z bokiem
, natomiast z bokiem 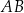 – kąt ostry, którego sinus jest równy
– kąt ostry, którego sinus jest równy  . Oblicz obwód czworokąta
. Oblicz obwód czworokąta 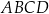 .
.
Czworokąt 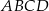 jest wpisany w okrąg o promieniu
jest wpisany w okrąg o promieniu 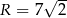 . Kąt
. Kąt 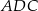 tego czworokąta jest ostry i jego miara jest o
tego czworokąta jest ostry i jego miara jest o 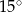 większa od miary kąta
większa od miary kąta 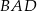 . Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta
. Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta 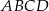 jest równy
jest równy  . Oblicz długości przekątnych
. Oblicz długości przekątnych 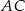 i
i 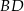 tego czworokąta.
tego czworokąta.
Na czworokącie wypukłym 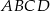 , w którym
, w którym 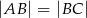 ,
, 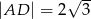 ,
, 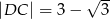 można opisać okrąg. Wiedząc, że przekątna
można opisać okrąg. Wiedząc, że przekątna 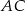 ma długość
ma długość 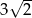 , oblicz pole tego czworokąta.
, oblicz pole tego czworokąta.
Czworokąt wypukły 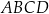 jest wpisany w okrąg o promieniu 4. Kąty
jest wpisany w okrąg o promieniu 4. Kąty 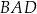 i
i 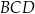 są proste (zobacz rysunek). Przekątne
są proste (zobacz rysunek). Przekątne 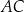 i
i 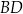 tego czworokąta przecinają się w punkcie
tego czworokąta przecinają się w punkcie 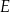 tak, że
tak, że 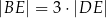 oraz
oraz 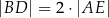 .
.

Oblicz długości boków czworokąta 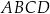 .
.
Czworokąt wypukły 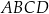 jest wpisany w okrąg o promieniu 9. Kąty
jest wpisany w okrąg o promieniu 9. Kąty 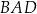 i
i 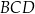 są proste (zobacz rysunek). Przekątne
są proste (zobacz rysunek). Przekątne 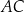 i
i 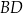 tego czworokąta przecinają się w punkcie
tego czworokąta przecinają się w punkcie 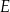 tak, że
tak, że  oraz
oraz 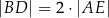 .
.

Oblicz długości boków czworokąta 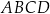 .
.
Dwusieczne kątów 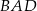 i
i 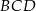 czworokąta wypukłego
czworokąta wypukłego 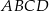 przecinają się w punkcie
przecinają się w punkcie 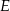 , przy czym punkty
, przy czym punkty 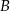 i
i 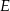 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 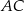 (zobacz rysunek).
(zobacz rysunek).
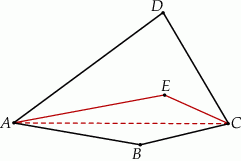
Wykaż, że 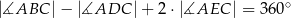 .
.
