Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku. Jaka figurę otrzymamy, łącząc kolejno środki boków: a) rombu, b) prostokąta, c) kwadratu?
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
Trapez równoramienny 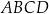 nie jest równoległobokiem. Przekątna
nie jest równoległobokiem. Przekątna 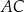 tego trapezu tworzy z podstawą
tego trapezu tworzy z podstawą 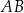 kąt o mierze
kąt o mierze 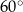 . Wykaż, że trapez
. Wykaż, że trapez 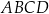 nie może być opisany na okręgu.
nie może być opisany na okręgu.
Czworokąt 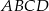 jest wpisany w okrąg oraz pola trójkątów
jest wpisany w okrąg oraz pola trójkątów 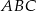 i
i 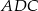 są równe. Wykaż, że
są równe. Wykaż, że
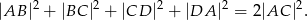
W czworokąt 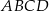 , w którym
, w którym 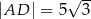 i
i 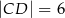 , można wpisać okrąg. Przekątna
, można wpisać okrąg. Przekątna 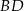 tworzy z bokiem
tworzy z bokiem 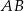 czworokąta kąt o mierze
czworokąta kąt o mierze 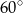 , natomiast z bokiem
, natomiast z bokiem 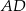 tworzy kąt, którego sinus jest równy
tworzy kąt, którego sinus jest równy  . Wyznacz długości boków
. Wyznacz długości boków 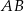 i
i 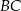 oraz długość przekątnej
oraz długość przekątnej 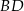 tego czworokąta.
tego czworokąta.
Przekątna 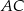 czworokąta
czworokąta 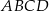 tworzy z bokiem
tworzy z bokiem 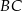 kąt
kąt 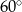 , a z bokiem
, a z bokiem 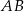 kąt
kąt 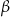 taki, że
taki, że 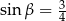 . Promień okręgu opisanego na trójkącie
. Promień okręgu opisanego na trójkącie 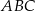 ma długość 5, a bok
ma długość 5, a bok 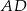 długość
długość 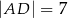 . Wiedząc, że w czworokąt
. Wiedząc, że w czworokąt 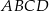 można wpisać okrąg oblicz długości pozostałych boków czworokąta oraz długość przekątnej
można wpisać okrąg oblicz długości pozostałych boków czworokąta oraz długość przekątnej 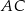 .
.
Na okręgu jest opisany czworokąt 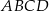 . Bok
. Bok 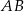 tego czworokąta jest trzy razy krótszy od przekątnej
tego czworokąta jest trzy razy krótszy od przekątnej 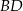 , a bok
, a bok 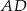 ma długość 10. Ponadto spełnione są następujące warunki:
ma długość 10. Ponadto spełnione są następujące warunki:
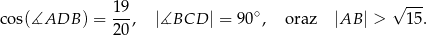
Oblicz długość boku 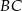 tego czworokąta.
tego czworokąta.
W czworokąt 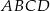 , w którym
, w którym 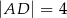 i
i 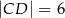 , można wpisać okrąg. Przekątna
, można wpisać okrąg. Przekątna 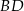 tworzy z bokiem
tworzy z bokiem 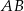 czworokąta kąt o mierze
czworokąta kąt o mierze 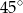 , natomiast z bokiem
, natomiast z bokiem 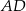 tworzy kąt, którego sinus jest równy
tworzy kąt, którego sinus jest równy 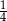 . Wyznacz długości boków
. Wyznacz długości boków 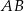 i
i 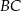 oraz długość przekątnej
oraz długość przekątnej 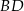 tego czworokąta.
tego czworokąta.
Na okręgu jest opisany czworokąt 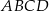 . Bok
. Bok 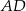 tego czworokąta jest dwa razy dłuższy od boku
tego czworokąta jest dwa razy dłuższy od boku 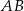 , a przekątna
, a przekątna 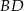 ma długość równą 6. Ponadto spełnione są następujące warunki:
ma długość równą 6. Ponadto spełnione są następujące warunki:
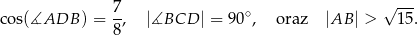
Oblicz długość boku 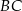 tego czworokąta.
tego czworokąta.
Na bokach 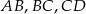 i
i 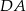 czworokąta
czworokąta 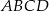 wybrano punkty
wybrano punkty 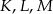 i
i 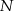 takie, że
takie, że
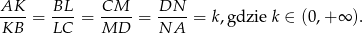
Oblicz stosunek pola czworokąta 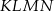 do pola czworokąta
do pola czworokąta 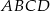 .
.
Czworokąt 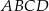 jest wpisany w okrąg o promieniu
jest wpisany w okrąg o promieniu 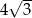 (patrz rysunek). Przekątna
(patrz rysunek). Przekątna 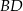 czworokąta ma długość 12. Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta jest równy
czworokąta ma długość 12. Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta jest równy 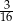 . Wiedząc, że
. Wiedząc, że 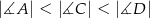 , oblicz miary kątów czworokąta
, oblicz miary kątów czworokąta 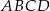 .
.
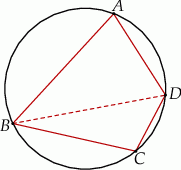
Czworokąt 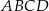 jest wpisany w okrąg o promieniu
jest wpisany w okrąg o promieniu 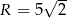 . Przekątna
. Przekątna 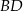 tego czworokąta ma długość 10. Kąty wewnętrzne
tego czworokąta ma długość 10. Kąty wewnętrzne 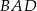 i
i 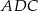 czworokąta
czworokąta 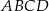 są ostre, a iloczyn sinusów wszystkich jego kątów wewnętrznych jest równy
są ostre, a iloczyn sinusów wszystkich jego kątów wewnętrznych jest równy  . Oblicz miary kątów wewnętrznych tego czworokąta.
. Oblicz miary kątów wewnętrznych tego czworokąta.
W czworokącie wypukłym 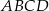 kąty przy wierzchołkach
kąty przy wierzchołkach 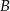 i
i 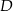 są proste (zobacz rysunek).
są proste (zobacz rysunek).
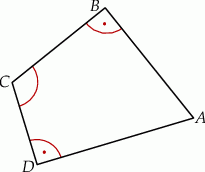
Oblicz sinus kąta przy wierzchołku 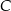 jeżeli
jeżeli 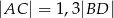 .
.
Dwa przeciwległe boki czworokąta wpisanego w okrąg mają równe długości. Wykaż, że czworokąt ten jest trapezem.
Dany jest czworokąt wypukły 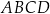 . Przekątne
. Przekątne 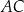 oraz
oraz 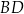 tego czworokąta przecinają się w punkcie
tego czworokąta przecinają się w punkcie 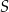 . Wykaż, że jeżeli
. Wykaż, że jeżeli 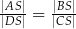 , to na czworokącie
, to na czworokącie 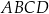 można opisać okrąg.
można opisać okrąg.
Dany jest czworokąt wypukły 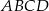 , w którym:
, w którym: 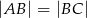 ,
, 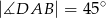 ,
, 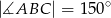 ,
, 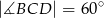 . Wykaż, że trójkąt
. Wykaż, że trójkąt 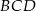 jest równoboczny.
jest równoboczny.
Na czworokącie 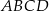 można opisać okrąg. Długości boków tego czworokąta są równe
można opisać okrąg. Długości boków tego czworokąta są równe 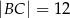 ,
, 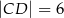 ,
, 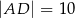 , a kąt
, a kąt 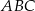 ma miarę
ma miarę 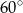 . Oblicz długość promienia okręgu opisanego na czworokącie
. Oblicz długość promienia okręgu opisanego na czworokącie 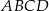 .
.
Oblicz pole czworokąta wypukłego 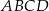 , w którym kąty wewnętrzne mają odpowiednio miary:
, w którym kąty wewnętrzne mają odpowiednio miary: 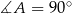 ,
, 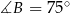 ,
, 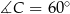 ,
, 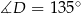 , a boki
, a boki 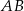 i
i 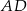 mają długość 3 cm. Sporządź rysunek pomocniczy.
mają długość 3 cm. Sporządź rysunek pomocniczy.
Przekątne czworokąta wypukłego 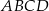 dzielą go na cztery trójkąty. Wykaż, że jeżeli promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt
dzielą go na cztery trójkąty. Wykaż, że jeżeli promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt 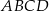 można wpisać okrąg.
można wpisać okrąg.
W czworokącie 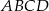 o obwodzie 24 dane są
o obwodzie 24 dane są 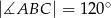 oraz
oraz 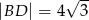 . Wiedząc, że środek przekątnej
. Wiedząc, że środek przekątnej 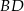 jest środkiem symetrii tego czworokąta oblicz jego pole.
jest środkiem symetrii tego czworokąta oblicz jego pole.
Przez każde dwa sąsiednie wierzchołki czworokąta 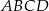 wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
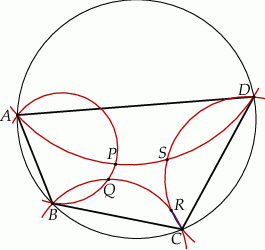
Wykaż, że punkty 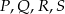 , w których przecinają się te okręgi, leżą na jednym okręgu.
, w których przecinają się te okręgi, leżą na jednym okręgu.
Czworokąt 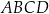 , w którym
, w którym 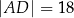 i
i 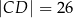 , jest opisany na okręgu. Kąt
, jest opisany na okręgu. Kąt 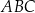 tego czworokąta jest rozwarty, a promień okręgu opisanego na trójkącie
tego czworokąta jest rozwarty, a promień okręgu opisanego na trójkącie 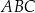 jest równy 12,5. Obwód czworokąta
jest równy 12,5. Obwód czworokąta 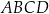 jest równy 66. Oblicz długość przekątnej
jest równy 66. Oblicz długość przekątnej 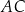 tego czworokąta.
tego czworokąta.
Dany jest czworokąt 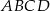 , którego kolejne boki mają długości 4,5,7,8. Kat między najkrótszymi bokami ma miarę
, którego kolejne boki mają długości 4,5,7,8. Kat między najkrótszymi bokami ma miarę  , taką że
, taką że 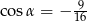 . Sprawdź czy na tym czworokącie można opisać okrąg.
. Sprawdź czy na tym czworokącie można opisać okrąg.
Dany jest czworokąt 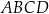 . Niech
. Niech 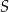 będzie punktem przecięcia jego przekątnych. Udowodnij, że czworokąt
będzie punktem przecięcia jego przekątnych. Udowodnij, że czworokąt 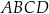 można wpisać w okrąg wtedy i tylko wtedy, gdy
można wpisać w okrąg wtedy i tylko wtedy, gdy 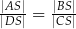 .
.
Obwód czworokąta wypukłego 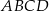 jest równy 50 cm. Obwód trójkąta
jest równy 50 cm. Obwód trójkąta 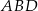 jest równy 46 cm, a obwód trójkąta
jest równy 46 cm, a obwód trójkąta 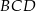 jest równy 36 cm. Oblicz długość przekątnej
jest równy 36 cm. Oblicz długość przekątnej 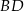 .
.
Przedłużenia przeciwległych boków czworokąta wpisanego w okrąg tworzą kąty ostre o miarach 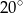 i
i 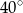 . Oblicz miary kątów czworokąta.
. Oblicz miary kątów czworokąta.

