Okrąg przecina boki czworokąta 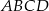 kolejno w punktach
kolejno w punktach 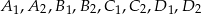 (zobacz rysunek).
(zobacz rysunek).
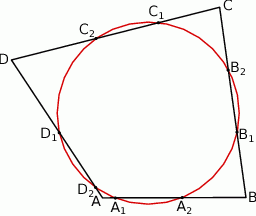
Wykaż, że jeżeli 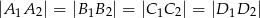 , to w czworokąt
, to w czworokąt  można wpisać okrąg.
można wpisać okrąg.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Okrąg przecina boki czworokąta 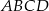 kolejno w punktach
kolejno w punktach 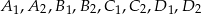 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że jeżeli 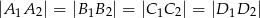 , to w czworokąt
, to w czworokąt 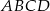 można wpisać okrąg.
można wpisać okrąg.
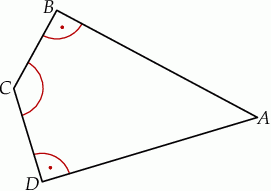
W czworokącie wypukłym 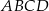 (zobacz rysunek poniżej) dane są kąty:
(zobacz rysunek poniżej) dane są kąty: 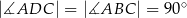 oraz
oraz 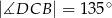 . Wykaż, że
. Wykaż, że 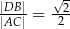 .
.
Przekątne czworokąta 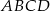 są prostopadłe. Wykaż, że
są prostopadłe. Wykaż, że 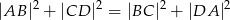 .
.
Dany jest czworokąt wypukły 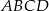 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 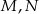 są odpowiednio środkami boków
są odpowiednio środkami boków 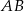 i
i 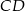 . Punkty
. Punkty 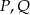 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 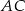 i
i 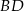 . Uzasadnij, że
. Uzasadnij, że 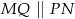 .
.
Dany jest czworokąt wypukły 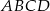 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 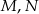 są odpowiednio środkami boków
są odpowiednio środkami boków 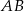 i
i 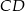 . Punkty
. Punkty 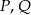 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 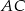 i
i 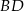 . Uzasadnij, że czworokąt
. Uzasadnij, że czworokąt 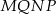 jest równoległobokiem.
jest równoległobokiem.
Wszystkie wierzchołki czworokąta 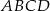 leżą na okręgu oraz
leżą na okręgu oraz 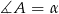 . Oblicz miarę kąta
. Oblicz miarę kąta 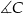 .
.
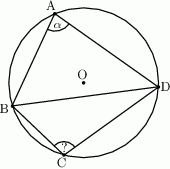
W okrąg o promieniu 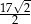 wpisano czworokąt
wpisano czworokąt 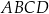 tak, że
tak, że 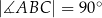 oraz
oraz 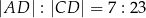 . Oblicz obwód czworokąta
. Oblicz obwód czworokąta 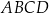 jeżeli jego pole jest równe 192.
jeżeli jego pole jest równe 192.
Przeciwległe boki czworokąta 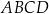 wpisanego w okrąg przecinają się w punktach
wpisanego w okrąg przecinają się w punktach 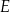 i
i 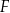 (zobacz rysunek), przy czym odcinek
(zobacz rysunek), przy czym odcinek 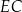 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 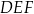 , a odcinek
, a odcinek 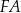 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 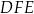 . Wykaż, że
. Wykaż, że 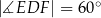 .
.

Dwusieczne czworokąta 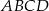 wpisanego w okrąg przecinają się w czterech różnych punktach:
wpisanego w okrąg przecinają się w czterech różnych punktach: 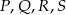 (zobacz rysunek).
(zobacz rysunek).
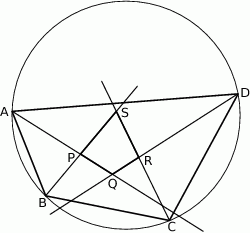
Wykaż, że na czworokącie 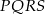 można opisać okrąg.
można opisać okrąg.
Z wierzchołków czworokąta 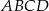 poprowadzono półproste, które przecinają się w wierzchołkach czworokąta
poprowadzono półproste, które przecinają się w wierzchołkach czworokąta 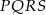 wpisanego w okrąg (zobacz rysunek).
wpisanego w okrąg (zobacz rysunek).
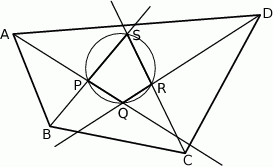
Wykaż, że jeżeli półproste 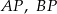 i
i 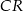 są dwusiecznymi odpowiednio kątów
są dwusiecznymi odpowiednio kątów 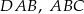 i
i 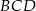 , to półprosta
, to półprosta 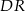 jest dwusieczną kąta
jest dwusieczną kąta 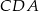 .
.
Długości boków czworokąta 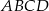 są równe:
są równe: 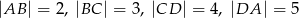 . Na czworokącie
. Na czworokącie 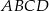 opisano okrąg. Oblicz długość przekątnej
opisano okrąg. Oblicz długość przekątnej 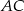 tego czworokąta.
tego czworokąta.
Długości boków czworokąta 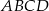 są równe:
są równe: 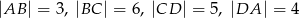 . Na czworokącie
. Na czworokącie 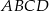 opisano okrąg. Oblicz długość przekątnej
opisano okrąg. Oblicz długość przekątnej 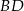 tego czworokąta.
tego czworokąta.
Wykaż, że jeżeli w czworokącie 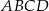 dwusieczne kątów przy wierzchołkach
dwusieczne kątów przy wierzchołkach 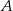 i
i 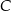 przecinają dwusieczne kątów przy wierzchołkach
przecinają dwusieczne kątów przy wierzchołkach 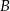 i
i 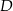 w czterech różnych punktach, to punkty te leżą na pewnym okręgu.
w czterech różnych punktach, to punkty te leżą na pewnym okręgu.
W czworokącie wypukłym 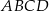 poprowadzono przekątną
poprowadzono przekątną 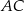 . Okręgi wpisane w trójkąty
. Okręgi wpisane w trójkąty 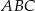 i
i 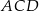 są styczne zewnętrznie. Wykaż, że w czworokąt
są styczne zewnętrznie. Wykaż, że w czworokąt 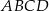 można wpisać okrąg.
można wpisać okrąg.
Przekątne czworokąta 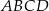 wpisanego w okrąg przecinają się w punkcie
wpisanego w okrąg przecinają się w punkcie 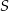 , a punkt
, a punkt 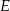 jest takim punktem przekątnej
jest takim punktem przekątnej 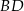 , że
, że 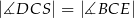 (zobacz rysunek).
(zobacz rysunek).
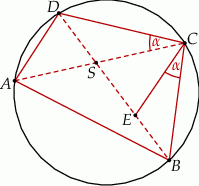
Wykaż, że 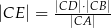 .
.
W czworokącie 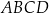 dane są długości boków:
dane są długości boków: 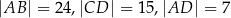 . Ponadto kąty
. Ponadto kąty 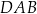 oraz
oraz 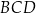 są proste. Oblicz pole tego czworokąta oraz długości jego przekątnych.
są proste. Oblicz pole tego czworokąta oraz długości jego przekątnych.
Udowodnij, że jeżeli środki boków dwóch czworokątów wypukłych pokrywają się, to pola tych czworokątów są równe.
W czworokącie 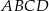 spełniony jest warunek
spełniony jest warunek 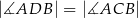 . Wykaż, że na czworokącie
. Wykaż, że na czworokącie 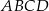 można opisać okrąg.
można opisać okrąg.
Dany jest czworokąt o kolejnych bokach długości 3,4,5 oraz kącie  między bokami długości 3 i 4 takim, że
między bokami długości 3 i 4 takim, że 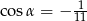 . Wyznacz długość czwartego boku, jeśli wiadomo, że na czworokącie można opisać okrąg.
. Wyznacz długość czwartego boku, jeśli wiadomo, że na czworokącie można opisać okrąg.
Czworokąt 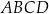 , w którym
, w którym 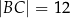 i
i 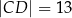 , jest opisany na okręgu. Przekątna
, jest opisany na okręgu. Przekątna 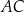 tego czworokąta tworzy z bokiem
tego czworokąta tworzy z bokiem 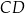 kąt, którego tangens jest równy
kąt, którego tangens jest równy 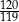 . Tangens kąta
. Tangens kąta 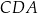 jest równy
jest równy 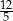 . Oblicz długość odcinka
. Oblicz długość odcinka 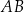 .
.
W czworokącie wypukłym 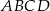 dane są długości jego boków i miara kąta
dane są długości jego boków i miara kąta 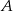 . Wyznacz miary pozostałych kątów tego czworokąta.
. Wyznacz miary pozostałych kątów tego czworokąta.
Wykaż, że jeżeli każda przekątna czworokąta wypukłego dzieli go na trójkąty o równych polach to czworokąt ten jest równoległobokiem.
W trójkącie 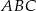 kąt wewnętrzny przy wierzchołku
kąt wewnętrzny przy wierzchołku 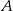 ma miarę
ma miarę 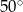 , a kąt wewnętrzny przy wierzchołku
, a kąt wewnętrzny przy wierzchołku 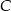 ma miarę
ma miarę 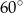 . Okrąg
. Okrąg 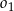 przechodzi przez punkt
przechodzi przez punkt 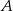 i przecina boki
i przecina boki 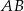 i
i 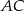 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 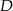 i
i 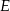 . Okrąg
. Okrąg 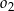 przechodzi przez punkt
przechodzi przez punkt 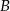 , przecina okrąg
, przecina okrąg 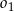 w punkcie
w punkcie 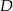 oraz w punkcie
oraz w punkcie 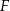 leżącym wewnątrz trójkąta
leżącym wewnątrz trójkąta 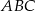 . Ponadto okrąg
. Ponadto okrąg 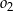 przecina bok
przecina bok 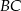 trójkąta w punkcie
trójkąta w punkcie 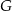 .
.
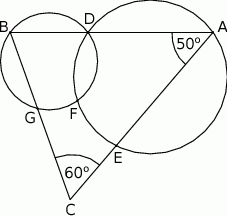
Udowodnij, że na czworokącie 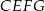 można opisać okrąg.
można opisać okrąg.
