Rzucamy raz sześcienną kostką do gry, a następnie rzucamy tyloma monetami, ile oczek wypadło na kostce. Oblicz prawdopodobieństwo tego, że dokładnie na jednej z wyrzuconych monet jest reszka. Wynik podaj w postaci ułamka nieskracalnego.
/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite
Wśród 390 pracowników pewnej firmy jest 150 kobiet i 240 mężczyzn. Wśród nich w wieku przedemerytalnym jest 21 kobiet i 43 mężczyzn. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrany pracownik tej firmy jest w wieku przedemerytalnym – pod warunkiem że jest mężczyzną.
Z trzech urn, w których jest po 2 kule białe i 3 czarne, wyjmujemy po jednej kuli i wkładamy do czwartej urny, w której była jedna kula biała. Losujemy teraz jedną kulę z czwartej urny. Oblicz prawdopodobieństwo, że z czwartej urny wyjmiemy białą kulę.
Zestaw tematów egzaminacyjnych składa się z 15 tematów z algebry, 15 z geometrii i 
tematów z prawdopodobieństwa. Z zestawu usunięto jeden temat, a następnie wylosowano z pozostałych jeden temat. Oblicz 
, jeśli wiadomo, że prawdopodobieństwo wylosowania tematu z prawdopodobieństwa wynosi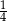 
.
Janek przeprowadza doświadczenie losowe, w którym jako wynik może otrzymać jedną z liczb: 0, 1, 2, 3, 4, 5, 6. Prawdopodobieństwo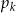 
otrzymania liczby 
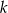jest dane wzorem: 
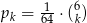. Rozważamy dwa zdarzenia:
– zdarzenie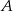 
polegające na otrzymaniu liczby ze zbioru 
,
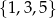– zdarzenie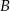 
polegające na otrzymaniu liczby ze zbioru 
.
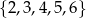Oblicz prawdopodobieństwo warunkowe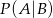 
W klasie IIIA jest 12 dziewcząt i 14 chłopców, natomiast w klasie IIIB jest 10 dziewcząt i 16 chłopców. Rzucamy cztery razy sześcienną kostką do gry. Jeśli suma wyrzuconych oczek jest liczbą parzystą i co najmniej na jednej kostce wypadła parzysta liczba oczek, to wybieramy trzyosobową delegację z klasy IIIA, w przeciwnym wypadku z klasy IIIB. Oblicz prawdopodobieństwo, że w skład delegacji wejdzie co najmniej jeden chłopiec.
Doświadczenie losowe polega na dziesięciokrotnym rzucie symetryczną monetą. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tym doświadczeniu losowym orzeł wypadł dokładnie trzy razy z rzędu, jeśli wiadomo, że wypadł dokładnie trzy razy.
W pudełku znajduje się 6 kul czarnych i 4 kule białe. Rzucamy dwa razy monetą. Jeśli otrzymamy 2 orły, losujemy z pudełka kolejno bez zwracania 2 kule. W pozostałych przypadkach losujemy jedną kulę. Oblicz prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna kula czarna.
Ukryj
Podobne zadania
W pudełku znajdują się 4 kule czarne i 6 kul białych. Rzucamy dwa razy monetą. Jeśli otrzymamy 2 reszki, losujemy z pudełka kolejno bez zwracania 2 kule. W pozostałych przypadkach losujemy trzy kule. Oblicz prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna kula czarna.
Karol i Antek grają w rzutki. Karol trafia w środek tarczy z prawdopodobieństwem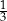 
, a Antek z prawdopodobieństwem 
. Rzucamy symetryczną, sześcienną kostką do gry. Jeżeli wypadnie liczba podzielna przez 3, to Karol dwa razy rzuca do tarczy. W przeciwnym wypadku Antek dwa razy rzuca do tarczy. Oblicz prawdopodobieństwa zdarzenia polegającego na tym, że w żadnym z tych dwóch wykonanych rzutów nie zostanie trafiony środek tarczy.
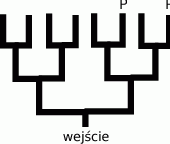
- Wpuszczony do labiryntu szczur, dochodząc do rozwidlenia dróg, dwa razy częściej skręca w lewo niż w prawo. Jakie jest prawdopodobieństwo tego, że dotrze do pokarmu (oznaczonego na rysunku
)? 
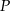- Inny szczur wpuszczony do tego samego labiryntu, dochodząc do rozwidlenia dróg, skręca w prawo w
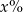przypadków. Oblicz 
, jeśli prawdopodobieństwo tego, że dotrze do pokarmu, jest równe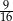 
.
Rzucamy dwukrotnie kostką do gry. Jakie jest prawdopodobieństwo, że suma wyrzuconych oczek jest większa niż 9, jeżeli wiadomo, że dokładnie jeden raz wypadło 6 oczek?
Wśród 10 tysięcy mieszkańców pewnego miasta przeprowadzono sondaż dotyczący budowy przedszkola publicznego. Wyniki sondażu przedstawiono w tabeli.
| Badane grupy | Liczba osób popierających budowę przedszkola | Liczba osób niepopierających budowy przedszkola |
| Kobiety | 5140 | 1860 |
| Mężczyźni | 2260 | 740 |
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, popiera budowę przedszkola, jeśli wiadomo, że jest mężczyzną.
Ukryj
Podobne zadania
Wśród 1200 uczniów pewnego liceum przeprowadzono sondaż dotyczący funkcjonowania sklepiku szkolnego. Wyniki sondażu przedstawiono w tabeli.
| Badane grupy | Liczba uczniów zadowolonych z asortymentu sklepiku | Liczba uczniów niezadowolonych z asortymentu sklepiku |
| Chłopcy | 320 | 260 |
| Dziewczęta | 280 | 340 |
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, jest zadowolona z asortymentu sklepiku, jeśli wiadomo, że jest dziewczynką.
Z talii 52 kart w czterech kolorach wybieramy losowo 2 karty. Oblicz prawdopodobieństwo, że wybrane karty to król i as, przy założeniu, że wybrane karty mają różne kolory.
W pierwszej urnie umieszczono 3 kule białe i 5 kul czarnych, a w drugiej urnie 7 kul białych i 4 kule czarne. Losujemy jedną kulę z pierwszej urny i przekładamy ją do drugiej urny. Następnie losujemy dwie kule z urny drugiej. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dwie kule wylosowane z drugiej urny są w różnych kolorach.
Mamy dwie talie kart po 24 karty. Z pierwszej talii losujemy jedną kartę i nie oglądając jej wkładamy do drugiej talii. Następnie z drugiej talii losujemy jedną kartę.
- Jakie jest prawdopodobieństwo wylosowania króla, jeżeli wiemy, że z pierwszej talii przełożono do drugiej trefla?
- Obliczyć prawdopodobieństwo, że wylosowana karta jest kierem.
- Wylosowana karta okazała się kierem. Jakie jest prawdopodobieństwo tego, że z pierwszej talii także został wylosowany kier?
Oblicz prawdopodobieństwo warunkowe, że w czterokrotnym rzucie symetryczną sześcienną kostką do gry otrzymamy co najmniej dwie „dwójki”, pod warunkiem że otrzymamy co najmniej jedną „piątkę”.
Urzędnik bankowy wie, że 12% kredytobiorców hipotecznych traci pracę i przestaje spłacać pożyczkę w ciągu 5 lat. Wie też, że 20% kredytobiorców hipotecznych traci pracę w ciągu 5 lat. Przy założeniu, że kredytobiorca hipoteczny stracił pracę, jakie jest prawdopodobieństwo, iż przestanie spłacać pożyczkę.
W loterii szkolnej losujemy jeden spośród 100 losów, przy czym w przypadku wyciągnięcia losu przegrywającego możemy wylosować jeszcze jeden los. Ile losów w tej loterii jest wygrywających, jeżeli prawdopodobieństwo wygranej jest równe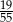 
?
Ukryj
Podobne zadania
W loterii szkolnej losujemy jeden spośród 100 losów, przy czym w przypadku wyciągnięcia losu przegrywającego możemy wylosować jeszcze jeden los. Ile losów w tej loterii jest przegrywających, jeżeli prawdopodobieństwo wygranej jest równe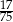 
?
Do koszyka włożono 12 jabłek, w tym dwa jabłka lobo. Po kilku dniach przechowywania z koszyka usunięto dwa popsute jabłka. Następnie losowo wybrano jedno jabłko. Oblicz prawdopodobieństwo, że wybrano jabłko lobo. Wynik podaj w postaci ułamka nieskracalnego.
Doświadczenie losowe polega na tym, że losujemy jednocześnie dwie liczby ze zbioru
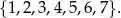
Oblicz prawdopodobieństwo warunkowe, że wśród wylosowanych liczb jest liczba 6, pod warunkiem, że suma wylosowanych liczb jest parzysta.
