Rzucamy dwa razy kostką do gry. Jeśli suma oczek wyrzuconych na obu kostkach jest liczbą podzielną przez 3, losujemy jedną liczbę ze zbioru 
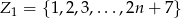, w przeciwnym przypadku losujemy jedną liczbę ze zbioru 
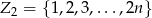. Oblicz prawdopodobieństwo wylosowania liczby parzystej.
/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite
Ze zbioru wszystkich liczb naturalnych czterocyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 4 lub 9, jeśli wiadomo, że jest ona podzielna przez 6.
Dwóch strzelców strzela do celu. Jeden trafia z prawdopodobieństwem 0,6, a drugi trafia z prawdopodobieństwem 0,8. Oblicz prawdopodobieństwo, że jeśli wykonają po jednym strzale, to cel zostanie trafiony dokładnie 1 raz.
Dwa zakłady pracy produkują takie same akumulatory, przy czym stosunek liczby akumulatorów produkowanych dziennie przez pierwszy zakład do liczby akumulatorów produkowanych dziennie przez drugi zakład jest równy 
. Badania wykazały, że niektóre z wyprodukowanych akumulatorów mają podwyższoną pojemność, przy czym własność tą ma 40% akumulatorów pochodzących z pierwszego zakładu i 30% akumulatorów pochodzących z drugiego zakładu. Oblicz jakie jest prawdopodobieństwo, że losowo wybrany akumulator pochodzący z dziennej produkcji obu zakładów nie ma podwyższonej pojemności.
W pudełku umieszczono 
kul (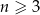
) wśród których dokładnie 2 kule są czarne, a pozostałe kule są białe. Z tego pudełka losujemy jedną kulę i odkładamy ją na bok. Jeżeli wylosowana kula jest biała, to do pudełka wrzucamy kulę czarną, a gdy wylosowana kula jest czarna, to do pudełka wrzucamy kulę białą. Po przeprowadzonej w ten sposób zmianie zawartości prawdopodobieństwo wylosowania kuli białej z tego pudełka jest równe 
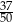. Oblicz 
.
Dane są dwie urny z kulami. W każdej z urn jest siedem kul. W pierwszej urnie są trzy kule czarne i cztery kule białe, w drugiej urnie są dwie kule czarne i pięć białych. Rzucamy jeden raz symetryczną monetą. Jeżeli wypadnie reszka, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – jedną kulę z drugiej urny. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tym doświadczeniu wylosujemy kulę białą.
Każda z urn oznaczonych liczbami 1, 2, 3 zawiera po 3 kule czarne i 4 białe, a każda urna oznaczona liczbami 4, 5, 6 zawiera po 3 czarne i 2 białe kule. Rzucamy sześcienną kostką do gry, a następnie z urny o numerze równym liczbie wyrzuconych oczek losujemy bez zwracania 2 kule. Co jest bardziej prawdopodobne: wylosowanie dwóch kul czarnych, czy dwóch kul białych?
W pudełku znajduje się 
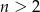sześciennych kostek do gry, przy czym 
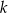spośród tych kostek (
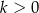i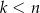 
) ma na dwóch ściankach jedno oczko, a na pozostałych czterech ściankach sześć oczek. Wybieramy losowo jedną z tych kostek i wykonujemy nią cztery kolejne rzuty. Oblicz jakie jest prawdopodobieństwo, że wybrana kostka miała jedno oczko na dwóch ściankach, jeżeli wiadomo, że w każdym z czterech wykonanych rzutów otrzymano ściankę z sześcioma oczkami.
Oblicz prawdopodobieństwo warunkowe, że w trzykrotnym rzucie symetryczną sześcienną kostką do gry otrzymamy co najmniej jedną „jedynkę”, pod warunkiem że otrzymamy co najmniej jedną „szóstkę”.
Na stu mężczyzn ośmiu, zaś na tysiąc kobiet pięć ma zaburzenie rozpoznawania barw. Z grupy, w której stosunek liczby mężczyzn do liczby kobiet wynosi 7:11 wybrano losowo jedną osobę. Jakie jest prawdopodobieństwo, że wylosowana osoba prawidłowo rozpoznaje kolory?
W pierwszej urnie umieszczono 3 kule białe i 5 kul czarnych, a w drugiej urnie 7 kul białych i 2 kule czarne. Losujemy jedną kulę z pierwszej urny, przekładamy ją do urny drugiej i dodatkowo dokładamy do urny drugiej jeszcze dwie kule tego samego koloru, co wylosowana kula. Następnie losujemy dwie kule z urny drugiej. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że obie kule wylosowane z drugiej urny będą białe.
Ukryj
Podobne zadania
W pierwszej urnie umieszczono 5 kul białych i 4 kule czarne, a w drugiej urnie 6 kul białych i 7 kul czarnych. Losujemy jedną kulę z pierwszej urny, przekładamy ją do urny drugiej i dodatkowo wyjmujemy z drugiej urny jeszcze dwie kule koloru innego, niż kolor wylosowanej kuli. Następnie losujemy dwie kule z urny drugiej. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że obie kule wylosowane z drugiej urny będą czarne.
W pierwszej urnie są 4 kule zielone i 5 czerwonych, w drugiej urnie 3 zielone i 6 czerwonych. Z pierwszej urny losujemy jedną kulę i przekładamy ją do drugiej urny. Następnie do drugiej urny dokładamy 2 kule tego samego koloru co wylosowana kula. Losujemy dwie kule z drugiej urny. Oblicz prawdopodobieństwo, że obie będą zielone.
Siedmiokrotnie rzucamy kostką do gry. Wśród otrzymanych wyników jest 5 czwórek. Jakie jest prawdopodobieństwo, że w pierwszym rzucie otrzymaliśmy czwórkę?
Ukryj
Podobne zadania
Sześciokrotnie rzucamy kostką do gry. Wśród otrzymanych wyników są dokładnie trzy dwójki. Jakie jest prawdopodobieństwo, że w pierwszym rzucie otrzymaliśmy piątkę?
Rzucamy sześcienną kostką do gry tak długo, aż otrzymamy co najmniej dwie nieparzyste liczby oczek, albo 10 parzystych liczb oczek. Oblicz prawdopodobieństwo, że w przeprowadzonym doświadczeniu otrzymaliśmy liczbę oczek równą 5, przy założeniu, że otrzymaliśmy tylko jedną nieparzystą liczbę oczek.
Dwie maszyny wykonują detale: pierwsza maszyna 75%, a druga 25%. Wśród detali maszyny pierwszej 95%, a maszyny drugiej 80% odpowiada wymogom technicznym. Wylosowano jeden detal, który odpowiada wymogom technicznym. Jakie jest prawdopodobieństwo, że detal ten pochodzi z maszyny drugiej?
Pewne doświadczenie polega na rzucie monetą i wylosowaniu jednej karty. Jeśli wypadnie reszka, to karta jest losowania z talii 52 kart, a jeśli wypadnie orzeł, to kartę losujemy z talii, z której usunięto wszystkie figury. Oblicz jakie jest prawdopodobieństwo:
- wylosowania króla;
- wylosowania króla trefl;
- wylosowania dwójki;
- wylosowania dwójki pik.
W dwóch pudełkach umieszczono po pięć kul, przy czym w pierwszym pudełku: 2 kule białe i 3 kule czerwone, a w drugim pudełku: 1 kulę białą i 4 kule czerwone. Z pierwszego pudełka losujemy jedną kulę i bez oglądania wkładamy ją do drugiego pudełka. Następnie losujemy jedną kulę z drugiego pudełka. Oblicz prawdopodobieństwo wylosowania kuli białej z drugiego pudełka.
W pewnym przedsiębiorstwie 9% wyrobów jest brakami. Na 100 dobrych wyrobów 70 jest pierwszego gatunku. Jakie jest prawdopodobieństwo, że wylosowany wyrób jest pierwszego gatunku?
W pojemniku ze słodyczami znajduje się 48 cukierków i 32 lizaki. Osiem lizaków i piętnaście cukierków ma smak jabłkowy, a pozostałe słodycze mają smak pomarańczowy. Z pojemnika wybrano losowo jeden słodycz (cukierek lub lizak) i okazało się, że ma smak pomarańczowy. Oblicz prawdopodobieństwo zdarzenia, że wybrany słodycz jest lizakiem.
Ze zbioru liczb 
losujemy kolejno bez zwracania dwie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3, jeżeli pierwsza z wylosowanych liczb jest liczbą pierwszą.
Oblicz prawdopodobieństwo warunkowe, że w czterokrotnym rzucie symetryczną sześcienną kostką do gry otrzymamy co najmniej jedną „czwórkę”, pod warunkiem że otrzymamy co najmniej jedną „piątkę”.
