Dany jest wielomian 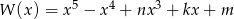 . Wyznacz wszystkie wartości parametrów
. Wyznacz wszystkie wartości parametrów 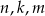 dla których reszta z dzielenia wielomianu
dla których reszta z dzielenia wielomianu 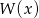 przez wielomian
przez wielomian 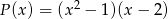 jest równa
jest równa 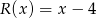 .
.
/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą/Przez stopnia 3
Wielomian 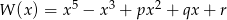 jest podzielny przez wielomian
jest podzielny przez wielomian 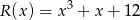 . Wyznacz liczby
. Wyznacz liczby 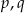 i
i  .
.
Wyznacz wszystkie wartości parametrów 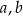 i
i  , dla których wielomian
, dla których wielomian
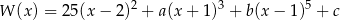
jest podzielny przez wielomian 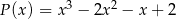 .
.
Wyznacz resztę z dzielenia wielomianu 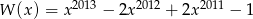 przez wielomian
przez wielomian 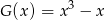 .
.
Wielomian 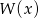 przy dzieleniu przez dwumiany
przy dzieleniu przez dwumiany 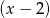 ,
, 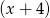 daje reszty odpowiednio równe -3 oraz -51. Wyznacz resztę z dzielenia wielomianu
daje reszty odpowiednio równe -3 oraz -51. Wyznacz resztę z dzielenia wielomianu 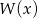 przez wielomian
przez wielomian 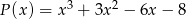 , wiedząc, że liczba -1 jest miejscem zerowym wielomianu
, wiedząc, że liczba -1 jest miejscem zerowym wielomianu 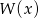 .
.
Wielomian 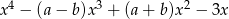 jest podzielny przez wielomian
jest podzielny przez wielomian 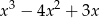 . Oblicz
. Oblicz  i
i 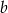 .
.
Wiedząc, że wielomian 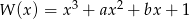 jest podzielny przez wielomian
jest podzielny przez wielomian 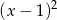 , oblicz
, oblicz  i
i 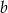 .
.
Wykaż, że jeżeli wielomian 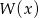 jest podzielny przez
jest podzielny przez 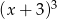 , to wielomian
, to wielomian 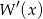 jest podzielny przez
jest podzielny przez 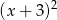 .
.
Wielomian 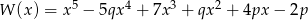 jest podzielny przez wielomian
jest podzielny przez wielomian 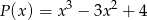 . Wyznacz
. Wyznacz 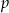 i
i 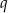 .
.
Wielomian 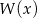 przy dzieleniu przez dwumiany
przy dzieleniu przez dwumiany 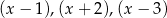 daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian
daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 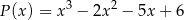 .
.
Przy dzieleniu wielomianu 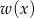 przez dwumian
przez dwumian 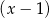 otrzymujemy resztę
otrzymujemy resztę 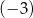 , przy dzieleniu przez dwumian
, przy dzieleniu przez dwumian 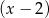 resztę 6, a przy dzieleniu przez dwumian
resztę 6, a przy dzieleniu przez dwumian 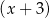 resztę 1. Wyznacz resztę z dzielenia wielomianu
resztę 1. Wyznacz resztę z dzielenia wielomianu 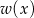 przez wielomian
przez wielomian 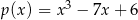 .
.
Wyznacz resztę 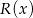 z dzielenia wielomianu
z dzielenia wielomianu 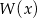 przez wielomian
przez wielomian 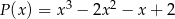 wiedząc, że
wiedząc, że 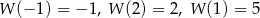 .
.
Wielomian 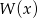 przy dzieleniu przez dwumiany
przy dzieleniu przez dwumiany 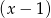 ,
, 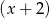 ,
, 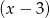 daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian
daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 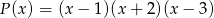 .
.

