Rzucamy trzy razy monetą, a następnie rzucamy tyle razy kostką, ile orłów otrzymaliśmy w rzutach monetami. Oblicz prawdopodobieństwo tego, że suma oczek otrzymanych w rzutach kostką jest dwa razy większa od liczby orłów otrzymanych w rzutach monetą jeżeli wiadomo, że w rzutach monetą otrzymaliśmy przynajmniej jednego orła.
/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite/Różne
Rzucamy raz sześcienną kostką do gry, a następnie rzucamy tyloma monetami, ile oczek wypadło na kostce. Oblicz prawdopodobieństwo tego, że dokładnie na jednej z wyrzuconych monet jest reszka. Wynik podaj w postaci ułamka nieskracalnego.
Zestaw tematów egzaminacyjnych składa się z 15 tematów z algebry, 15 z geometrii i 
tematów z prawdopodobieństwa. Z zestawu usunięto jeden temat, a następnie wylosowano z pozostałych jeden temat. Oblicz 
, jeśli wiadomo, że prawdopodobieństwo wylosowania tematu z prawdopodobieństwa wynosi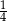 
.
W pudełku znajduje się 6 kul czarnych i 4 kule białe. Rzucamy dwa razy monetą. Jeśli otrzymamy 2 orły, losujemy z pudełka kolejno bez zwracania 2 kule. W pozostałych przypadkach losujemy jedną kulę. Oblicz prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna kula czarna.
Ukryj
Podobne zadania
W pudełku znajdują się 4 kule czarne i 6 kul białych. Rzucamy dwa razy monetą. Jeśli otrzymamy 2 reszki, losujemy z pudełka kolejno bez zwracania 2 kule. W pozostałych przypadkach losujemy trzy kule. Oblicz prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna kula czarna.
Karol i Antek grają w rzutki. Karol trafia w środek tarczy z prawdopodobieństwem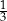 
, a Antek z prawdopodobieństwem 
. Rzucamy symetryczną, sześcienną kostką do gry. Jeżeli wypadnie liczba podzielna przez 3, to Karol dwa razy rzuca do tarczy. W przeciwnym wypadku Antek dwa razy rzuca do tarczy. Oblicz prawdopodobieństwa zdarzenia polegającego na tym, że w żadnym z tych dwóch wykonanych rzutów nie zostanie trafiony środek tarczy.
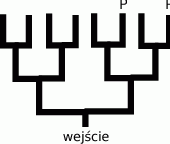
- Wpuszczony do labiryntu szczur, dochodząc do rozwidlenia dróg, dwa razy częściej skręca w lewo niż w prawo. Jakie jest prawdopodobieństwo tego, że dotrze do pokarmu (oznaczonego na rysunku
)? 
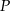- Inny szczur wpuszczony do tego samego labiryntu, dochodząc do rozwidlenia dróg, skręca w prawo w
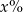przypadków. Oblicz 
, jeśli prawdopodobieństwo tego, że dotrze do pokarmu, jest równe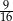 
.
Do koszyka włożono 12 jabłek, w tym dwa jabłka lobo. Po kilku dniach przechowywania z koszyka usunięto dwa popsute jabłka. Następnie losowo wybrano jedno jabłko. Oblicz prawdopodobieństwo, że wybrano jabłko lobo. Wynik podaj w postaci ułamka nieskracalnego.
W fabryce obuwia pracuje pięć linii produkcyjnych produkujących ten sam model butów. W poniższej tabeli zawarto informacje o wydajności tych linii oraz o odsetku wadliwych par obuwia produkowanych przez każdą z nich.
| Linia produkcyjna | Wydajność | Odsetek wadliwych par |
| I | 60 par/godzinę | 2% |
| II | 50 par/godzinę | 3% |
| III | 40 par/godzinę | 1% |
| IV | 80 par/godzinę | 3% |
| V | 70 par/godzinę | 2% |
Wybieramy losowo jedną parę obuwia wyprodukowaną przez te linie produkcyjne. Jakie jest prawdopodobieństwo, że wybrana para nie okaże się wadliwa?
Dwóch strzelców strzela do celu. Jeden trafia z prawdopodobieństwem 0,6, a drugi trafia z prawdopodobieństwem 0,8. Oblicz prawdopodobieństwo, że jeśli wykonają po jednym strzale, to cel zostanie trafiony dokładnie 1 raz.
Dwa zakłady pracy produkują takie same akumulatory, przy czym stosunek liczby akumulatorów produkowanych dziennie przez pierwszy zakład do liczby akumulatorów produkowanych dziennie przez drugi zakład jest równy 
. Badania wykazały, że niektóre z wyprodukowanych akumulatorów mają podwyższoną pojemność, przy czym własność tą ma 40% akumulatorów pochodzących z pierwszego zakładu i 30% akumulatorów pochodzących z drugiego zakładu. Oblicz jakie jest prawdopodobieństwo, że losowo wybrany akumulator pochodzący z dziennej produkcji obu zakładów nie ma podwyższonej pojemności.
Dane są dwie urny z kulami. W każdej z urn jest siedem kul. W pierwszej urnie są trzy kule czarne i cztery kule białe, w drugiej urnie są dwie kule czarne i pięć białych. Rzucamy jeden raz symetryczną monetą. Jeżeli wypadnie reszka, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – jedną kulę z drugiej urny. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tym doświadczeniu wylosujemy kulę białą.
Dwie maszyny wykonują detale: pierwsza maszyna 75%, a druga 25%. Wśród detali maszyny pierwszej 95%, a maszyny drugiej 80% odpowiada wymogom technicznym. Wylosowano jeden detal, który odpowiada wymogom technicznym. Jakie jest prawdopodobieństwo, że detal ten pochodzi z maszyny drugiej?
Pewne doświadczenie polega na rzucie monetą i wylosowaniu jednej karty. Jeśli wypadnie reszka, to karta jest losowania z talii 52 kart, a jeśli wypadnie orzeł, to kartę losujemy z talii, z której usunięto wszystkie figury. Oblicz jakie jest prawdopodobieństwo:
- wylosowania króla;
- wylosowania króla trefl;
- wylosowania dwójki;
- wylosowania dwójki pik.
W pewnym przedsiębiorstwie 9% wyrobów jest brakami. Na 100 dobrych wyrobów 70 jest pierwszego gatunku. Jakie jest prawdopodobieństwo, że wylosowany wyrób jest pierwszego gatunku?
