Ramię trapezu równoramiennego 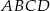 ma długość
ma długość 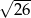 . Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Równoramienny
Wysokość trapezu równoramiennego ma długość 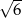 , a jedna z podstaw jest trzy razy dłuższa od drugiej. Oblicz pole trapezu wiedząc, że sinus jego kąta ostrego jest równy 0,2.
, a jedna z podstaw jest trzy razy dłuższa od drugiej. Oblicz pole trapezu wiedząc, że sinus jego kąta ostrego jest równy 0,2.
Wykaż, że jeśli przekątna trapezu równoramiennego zawiera się w dwusiecznej jego kąta ostrego, to ramię jest równe krótszej podstawie.
Obwód trapezu równoramiennego wynosi 32 cm. Wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach 3 cm i 11 cm. Oblicz pole trapezu.
Obwód trapezu równoramiennego wynosi 50 cm. Wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach 5 cm i 12 cm. Oblicz pole trapezu.
Przekątne trapezu równoramiennego 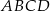 przecinają się w punkcie
przecinają się w punkcie 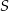 . Przekątna
. Przekątna 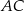 tworzy z dłuższą podstawą
tworzy z dłuższą podstawą 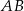 kąt
kąt  i z ramieniem
i z ramieniem 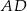 kąt
kąt 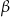 takie, że
takie, że 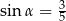 i
i 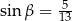 . Pole trapezu
. Pole trapezu 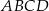 jest równe 448. Oblicz pole trójkąta
jest równe 448. Oblicz pole trójkąta 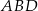 .
.
W trapezie równoramiennym 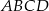 przekątna
przekątna 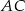 jest prostopadła do ramienia i tworzy z dłuższą podstawą
jest prostopadła do ramienia i tworzy z dłuższą podstawą 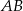 trapezu kąt o mierze
trapezu kąt o mierze 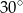 . Oblicz pole powierzchni tego trapezu wiedząc, że długość przekątnej
. Oblicz pole powierzchni tego trapezu wiedząc, że długość przekątnej 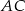 wynosi
wynosi 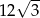 .
.
W trapezie równoramiennym 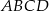 przekątna
przekątna 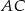 jest prostopadła do ramienia. Kąt ostry trapezu ma miarę
jest prostopadła do ramienia. Kąt ostry trapezu ma miarę 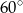 . Oblicz pole powierzchni tego trapezu wiedząc, że długość przekątnej
. Oblicz pole powierzchni tego trapezu wiedząc, że długość przekątnej 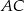 wynosi
wynosi 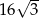 .
.
Oblicz wysokość i przekątną trapezu równoramiennego o podstawach 21 cm i 11 cm oraz ramieniu równym 13 cm.
W trapezie równoramiennym 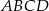 ramię ma długość 10. Obwód tego trapezu jest równy 40. Wiedząc, że tangens kąta ostrego w trapezie
ramię ma długość 10. Obwód tego trapezu jest równy 40. Wiedząc, że tangens kąta ostrego w trapezie 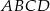 jest równy
jest równy  , oblicz długości jego podstaw.
, oblicz długości jego podstaw.
W trapezie równoramiennym 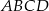 ramię ma długość 13. Obwód tego trapezu jest równy 52. Wiedząc, że tangens kąta ostrego w trapezie
ramię ma długość 13. Obwód tego trapezu jest równy 52. Wiedząc, że tangens kąta ostrego w trapezie 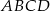 jest równy
jest równy 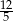 , oblicz długości jego podstaw.
, oblicz długości jego podstaw.
Dany jest trapez równoramienny 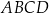 , w którym podstawa
, w którym podstawa 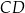 ma długość 6, ramię
ma długość 6, ramię 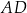 ma długość 4, a kąty
ma długość 4, a kąty 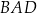 oraz
oraz 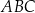 mają miarę
mają miarę 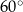 (zobacz rysunek).
(zobacz rysunek).
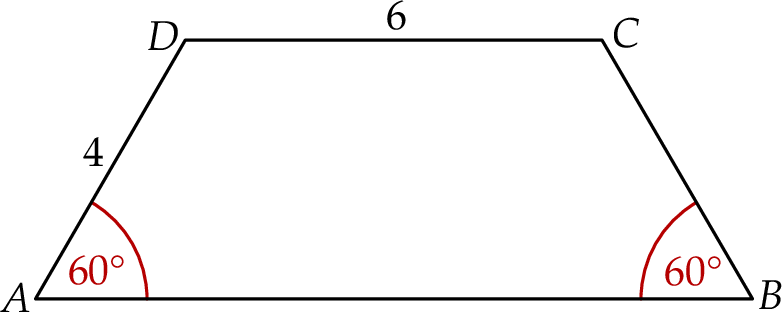
Oblicz pole tego trapezu.
Dany jest trapez równoramienny 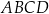 , w którym podstawa
, w którym podstawa 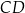 ma długość 8, ramię
ma długość 8, ramię 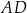 ma długość 6, a kąty
ma długość 6, a kąty 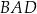 oraz
oraz 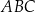 mają miarę
mają miarę 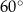 (zobacz rysunek).
(zobacz rysunek).
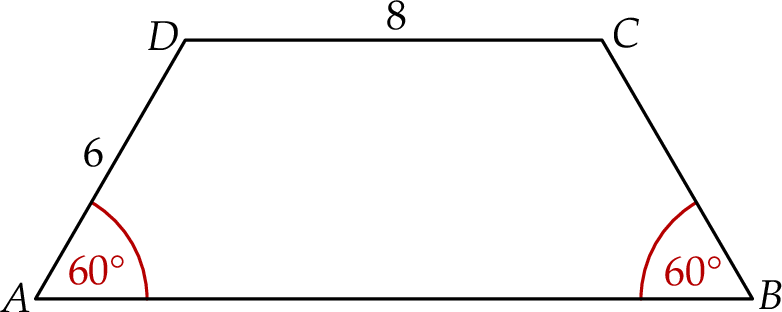
Oblicz pole tego trapezu.
W trapezie równoramiennym 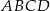 krótsza podstawa
krótsza podstawa 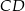 ma długość równą 6 i jest równa wysokości trapezu. Długość dłuższej podstawy
ma długość równą 6 i jest równa wysokości trapezu. Długość dłuższej podstawy 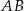 jest równa długości przekątnej trapezu. Oblicz pole tego trapezu.
jest równa długości przekątnej trapezu. Oblicz pole tego trapezu.
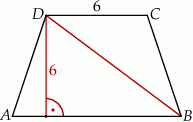
W trapezie równoramiennym o podstawach długości 20 i 40, oraz kącie ostrym o mierze 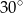 połączono środki wszystkich boków. Oblicz pole otrzymanego czworokąta.
połączono środki wszystkich boków. Oblicz pole otrzymanego czworokąta.
Podstawy trapezu równoramiennego mają długości  i
i 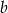 , a jego przekątna ma długość
, a jego przekątna ma długość 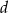 . Wyznacz cosinus kąta między przekątnymi tego trapezu.
. Wyznacz cosinus kąta między przekątnymi tego trapezu.
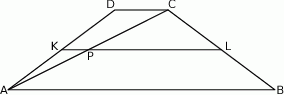
W trapezie równoramiennym 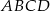 punkty
punkty 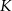 i
i 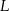 są odpowiednio środkami ramion
są odpowiednio środkami ramion 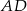 i
i 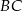 . Przekątna
. Przekątna 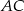 przecina odcinek
przecina odcinek 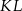 w punkcie
w punkcie 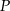 . Wiedząc, że
. Wiedząc, że 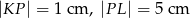 oraz wysokość trapezu jest równa 3 cm, oblicz długość boków trapezu.
oraz wysokość trapezu jest równa 3 cm, oblicz długość boków trapezu.
W trapezie równoramiennym 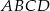 , wysokość
, wysokość 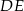 ma długość 6 cm. Punkt
ma długość 6 cm. Punkt 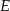 dzieli dłuższą podstawę
dzieli dłuższą podstawę 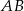 na dwa odcinki. Wiedząc, że
na dwa odcinki. Wiedząc, że 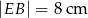 , oblicz pole trapezu
, oblicz pole trapezu 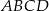 .
.
W trapezie równoramiennym 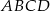 przekątna
przekątna 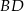 jest prostopadła do ramienia
jest prostopadła do ramienia 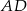 (zobacz rysunek). Podstawy trapezu mają długość:
(zobacz rysunek). Podstawy trapezu mają długość: 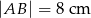 i
i 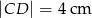 . Oblicz pole oraz miary kątów trapezu.
. Oblicz pole oraz miary kątów trapezu.
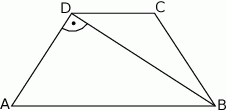
W trapezie równoramiennym 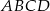 przekątna
przekątna 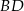 jest prostopadła do ramienia
jest prostopadła do ramienia 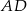 (zobacz rysunek). Podstawy trapezu mają długość:
(zobacz rysunek). Podstawy trapezu mają długość: 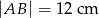 i
i 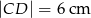 . Oblicz pole oraz miary kątów trapezu.
. Oblicz pole oraz miary kątów trapezu.
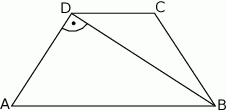
Oblicz pole trapezu równoramiennego o podstawach długości 10 cm i 6 cm oraz przekątnej o długości 9 cm.
W trapezie równoramiennym 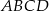 , w którym
, w którym 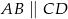 , dane są
, dane są 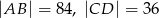 ,
, 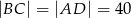 . Oblicz promień okręgu wpisanego w trójkąt
. Oblicz promień okręgu wpisanego w trójkąt 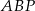 , gdzie
, gdzie 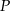 jest punktem przecięcia przekątnych tego trapezu.
jest punktem przecięcia przekątnych tego trapezu.
W trapezie równoramiennym przekątna ma długość 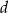 i tworzy z dłuższą podstawą kąt o mierze
i tworzy z dłuższą podstawą kąt o mierze  . Wykaż, że pole tego trapezu jest równe
. Wykaż, że pole tego trapezu jest równe 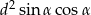 .
.
Stosunek długości boków trapezu równoramiennego wynosi 17:13:7:13. Oblicz obwód trapezu wiedząc, że jego pole jest równe 36.
W trapezie równoramiennym, którego podstawy mają długość  i
i 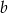 (
(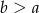 ), kąt ostry ma miarę
), kąt ostry ma miarę  , połączono odcinkami środki sąsiednich boków. Oblicz pole powstałego czworokąta.
, połączono odcinkami środki sąsiednich boków. Oblicz pole powstałego czworokąta.

