Na bokach 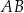 i
i 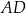 rombu
rombu 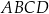 wybrano odpowiednio punkty
wybrano odpowiednio punkty 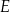 i
i 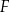 tak, że
tak, że 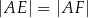 . Pole pięciokąta
. Pole pięciokąta 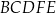 jest 17 razy większe niż pole trójkąta
jest 17 razy większe niż pole trójkąta 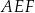 . Punkt
. Punkt 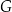 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 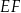 i przekątnej
i przekątnej 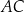 . Oblicz Oblicz
. Oblicz Oblicz 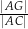 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
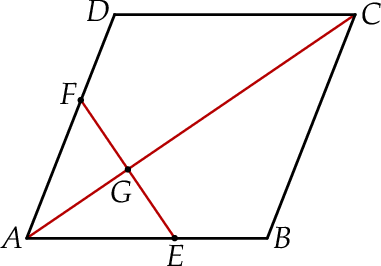
Na bokach 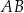 i
i 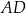 rombu
rombu 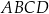 wybrano odpowiednio punkty
wybrano odpowiednio punkty 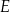 i
i 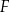 tak, że
tak, że 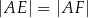 . Pole pięciokąta
. Pole pięciokąta 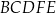 jest 17 razy większe niż pole trójkąta
jest 17 razy większe niż pole trójkąta 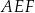 . Punkt
. Punkt 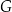 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 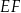 i przekątnej
i przekątnej 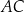 . Oblicz Oblicz
. Oblicz Oblicz 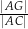 .
.

Pole rombu jest równe 120. Gdyby zwiększyć długości jego przekątnych odpowiednio o 2 i 5 to pole wzrosłoby o 55. Oblicz obwód rombu. Podaj wszystkie możliwe odpowiedzi.
Bok rombu 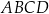 ma długość
ma długość  , a sinus jego kąta ostrego
, a sinus jego kąta ostrego 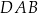 jest równy
jest równy 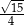 . Na bokach
. Na bokach 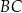 i
i 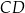 wybrano punkty
wybrano punkty 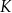 i
i 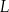 odpowiednio tak, że odcinki
odpowiednio tak, że odcinki 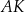 i
i 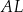 podzieliły pole rombu
podzieliły pole rombu 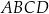 na trzy równe części (zobacz rysunek).
na trzy równe części (zobacz rysunek).
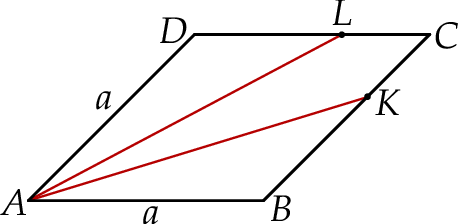
Oblicz długość odcinka 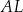 .
.
Bok rombu 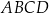 ma długość
ma długość  , a kąt ostry przy wierzchołku
, a kąt ostry przy wierzchołku 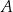 ma miarę
ma miarę 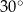 . Oblicz długość odcinka łączącego wierzchołek
. Oblicz długość odcinka łączącego wierzchołek 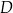 rombu z punktem boku
rombu z punktem boku 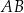 , dzielącego ten bok w stosunku
, dzielącego ten bok w stosunku 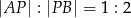 .
.
Oblicz długość boku rombu wiedząc, że prosta poprowadzona przez jeden z jego wierzchołków odcina na przedłużeniach dwóch jego boków odcinki o długościach 4 i 9.
Obwód rombu wynosi 18 cm, a jego pole 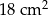 . Oblicz wysokość tego rombu.
. Oblicz wysokość tego rombu.
Bok rombu ma długość 13 cm, a jedna z jego przekątnych ma długość 24 cm. Oblicz długość drugiej przekątnej.
Jedna z przekątnych rombu jest dwa razy dłuższa od drugiej. Wyznacz stosunek obwodu rombu do sumy jego przekątnych.
Oblicz sumę długości przekątnych rombu wiedząc, że suma ich kwadratów jest równa 313, a pole rombu jest równe 78.
Znajdź długości przekątnych rombu o boku 29 jeżeli wiadomo, że ich różnica długości jest równa 2.
Jaką wysokość ma romb, jeżeli wiadomo, że jego przekątne mają długości 12 i 16 centymetrów?
Jaką wysokość ma romb, jeżeli wiadomo, że jego przekątne mają długości 16 i 30?
Pole rombu jest równe 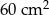 . Dłuższa przekątna rombu podzieliła kąt ostry rombu na takie dwa kąty o mierze
. Dłuższa przekątna rombu podzieliła kąt ostry rombu na takie dwa kąty o mierze  , że
, że 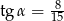 . Oblicz długość boku rombu.
. Oblicz długość boku rombu.
W rombie jedna z przekątnych jest dłuższa od drugiej o 3 cm. Dla jakich długości przekątnych pole rombu jest większe od 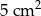 ?
?
Dany jest romb, którego kąt ostry ma miarę 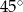 , a jego pole jest równe
, a jego pole jest równe 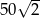 . Oblicz wysokość tego rombu.
. Oblicz wysokość tego rombu.
Dany jest romb, którego kąt ostry ma miarę 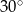 , a jego pole jest równe
, a jego pole jest równe 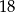 . Oblicz wysokość tego rombu.
. Oblicz wysokość tego rombu.
