Wykres funkcji 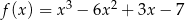 przesunięto o wektor
przesunięto o wektor 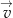 i wyniku tej operacji otrzymano wykres, który jest symetryczny względem początku układu współrzędnych. Wyznacz współrzędne wektora
i wyniku tej operacji otrzymano wykres, który jest symetryczny względem początku układu współrzędnych. Wyznacz współrzędne wektora 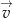 .
.
/Szkoła średnia/Funkcje - wykresy/Wielomiany
Na wykresie przedstawiono fragment wykresu wielomianu 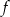 stopnia 3.
stopnia 3.
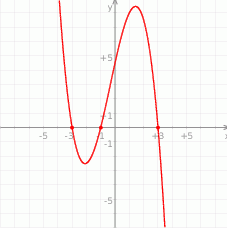
Widząc, że 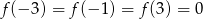 oraz
oraz 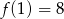 wykaż, że
wykaż, że 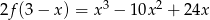 .
.
Wyznacz punkty wspólne wykresu wielomianu 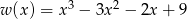 i prostej
i prostej 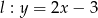 .
.
Wyznacz punkty wspólne wykresu wielomianu 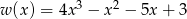 i prostej
i prostej 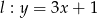 .
.
Wyznacz punkty wspólne wykresu wielomianu 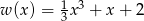 i prostej
i prostej 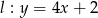 .
.
Dany jest wielomian 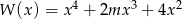 z parametrem
z parametrem 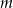 .
.
- Wiedząc, że wykres tego wielomianu jest symetryczny względem prostej
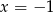 , wyznacz
, wyznacz 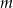 .
. - Dla wyznaczonej wartości parametru
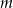 uzasadnij, że nierówność
uzasadnij, że nierówność 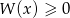 jest spełniona przez każdą liczbę rzeczywistą
jest spełniona przez każdą liczbę rzeczywistą 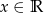 .
.
Korzystając z danego wykresu funkcji 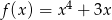 naszkicuj wykres funkcji
naszkicuj wykres funkcji 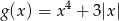 .
.
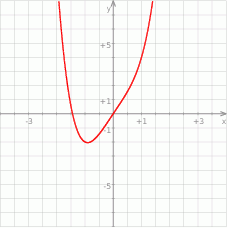
Korzystając z danego wykresu funkcji 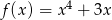 naszkicuj wykres funkcji
naszkicuj wykres funkcji 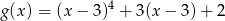 .
.
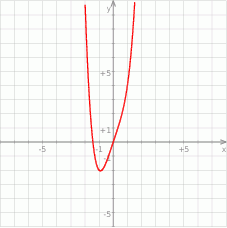
Korzystając z danego wykresu funkcji 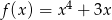 naszkicuj wykres funkcji
naszkicuj wykres funkcji 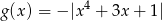 .
.
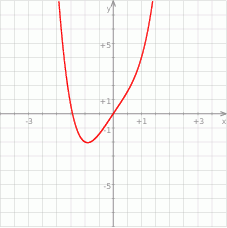
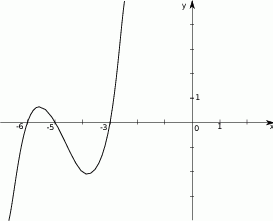
Na rysunku przedstawiony jest wykres pewnego wielomianu  stopnia trzeciego.
stopnia trzeciego.
- Czy wielomian
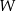 jest podzielny przez wielomian
jest podzielny przez wielomian 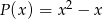 ?
? - Napisz wzór wielomianu
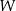 .
.
Wyznacz punkty wspólne wykresu wielomianu 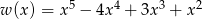 i prostej
i prostej 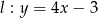 .
.
Wyznacz punkty wspólne wykresów funkcji 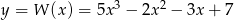 oraz
oraz 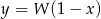 .
.
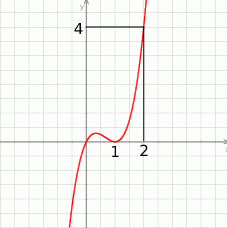
Wielomian stopnia trzeciego 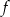 , którego fragment wykresu przedstawiono na poniższym rysunku spełnia warunek
, którego fragment wykresu przedstawiono na poniższym rysunku spełnia warunek 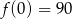 .
.
Wielomian 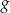 dany jest wzorem
dany jest wzorem 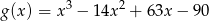 . Wykaż, że
. Wykaż, że 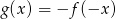 dla
dla 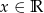 .
.
Wykres funkcji 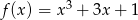 przekształcono w symetrii względem prostej
przekształcono w symetrii względem prostej 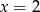 i otrzymano wykres funkcji
i otrzymano wykres funkcji 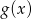 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 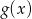 .
.
Funkcja 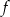 określona jest wzorem
określona jest wzorem 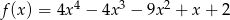 .
.
- Znajdź punkt przecięcia wykresu funkcji
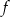 z osia
z osia 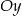 .
. - Znajdź, o ile istnieją, punkty przecięcia funkcji
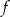 z osia
z osia 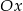 .
. - Wyznacz te argumenty, dla których funkcje
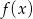 i funkcja
i funkcja 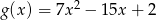 przyjmują tę samą wartość.
przyjmują tę samą wartość.

