Kąty/Równoramienny/Trójkąt - zadania z matematyki

/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny/Kąty

W trójkącie równoramiennym 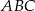ABC , w którym 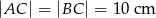|AC | = |BC | = 10 cm , wysokość poprowadzona z wierzchołka 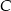jest równa 5 cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w stopniach.

Dany jest trójkąt 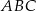ABC , w którym 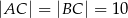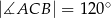|AC | = |BC | = 10 , ∘ |∡ACB | = 1 20 . Na boku 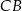obrano punkt 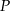dzielący ten bok w stosunku 3:2 (licząc od punktu 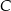). Oblicz sinus kąta PAB .

Ukryj Podobne zadania

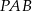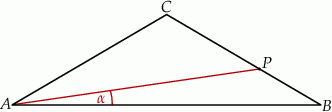
W trójkącie równoramiennym 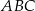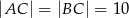ABC : |AC | = |BC | = 10 , a miara kąta 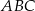ABC jest równa 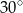30∘ . Na boku 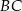wybrano punkt 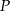, taki, że 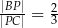|BP|= 2 |PC| 3 . Oblicz sinus kąta (zobacz rysunek).

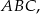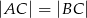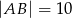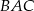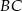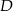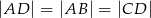W trójkącie równoramiennym ABC , w którym |AC | = |BC | i |AB | = 10 , poprowadzono dwusieczną kąta BAC przecinająca bok w punkcie . Wówczas okazało się, że |AD | = |AB | = |CD | .

Wyznacz miary kątów trójkąta .
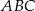Oblicz długość ramienia .
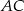Oblicz .

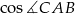W trójkącie równoramiennym środkowe ramion są prostopadłe. Oblicz cosinus kąta między ramionami.

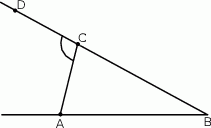
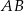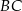Odcinki oraz (rysunek) są równej długości. Kąt 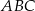ABC ma miarę o 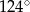12 4∘ mniejszą od miary kąta do niego przyległego. Oblicz miarę kąta ACD .

Ukryj Podobne zadania

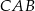Odcinki oraz (rysunek) są równej długości. Kąt CAB ma miarę o 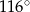11 6∘ mniejszą od miary kąta do niego przyległego. Oblicz miarę kąta BCD .

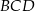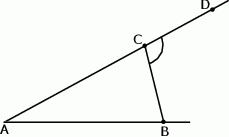
Dany jest trójkąt równoramienny 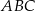ABC , w którym podstawa 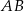ma długość 12, a każde z ramion 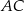i 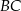ma długość równą 10. Punkt jest środkiem ramienia (zobacz rysunek).

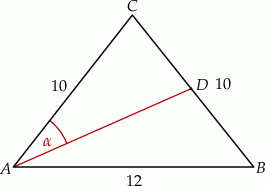
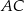Oblicz sinus kąta , jaki środkowa tworzy z ramieniem trójkąta ABC .

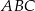Punkt 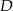leży na boku 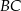trójkąta równoramiennego 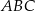ABC , w którym |AC | = |BC | .

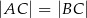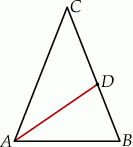
Odcinek 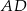dzieli trójkąt 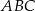ABC na dwa trójkąty równoramienne w taki sposób, że 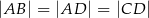|AB | = |AD | = |CD | . Oblicz miary kątów trójkąta ABC .

Ukryj Podobne zadania

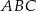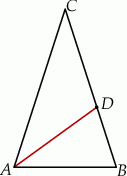
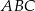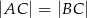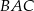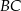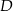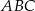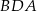Dany jest trójkąt równoramienny ABC , w którym |AC | = |BC | . Dwusieczna kąta BAC przecina bok w takim punkcie , że trójkąty ABC i BDA są podobne (zobacz rysunek). Oblicz miarę kąta BAC .

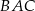Podstawą trójkąta równoramiennego 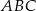ABC jest średnica 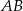okręgu, którego środkiem jest punkt 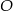. Punkty 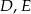D ,E są punktami przecięcia ramion 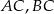AC ,BC trójkąta z okręgiem. Miara kąta 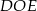DOE jest równa 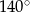140 ∘ . Wykaż, że miara kąta 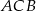ACB jest równa 20∘ .

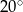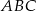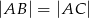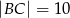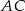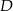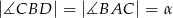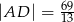Dany jest trójkąt równoramienny ABC , w którym |AB | = |AC | i |BC | = 10 . Na boku wybrano punkt w ten sposób, że |∡CBD | = |∡BAC | = α oraz |AD | = 6193 . Oblicz sin α .

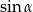Ostrokątny trójkąt równoramienny 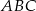ABC o podstawie 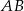jest wpisany w okrąg o środku 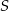, przy czym kąt 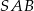SAB ma miarę 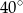4 0∘ . Oblicz miarę kąta CAB .

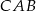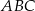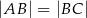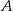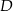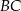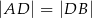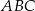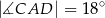W trójkącie ABC , w którym |AB | = |BC | połączono wierzchołek punktem na boku w ten sposób, że |AD | = |DB | . Wyznacz miary kątów trójkąta ABC jeżeli |∡CAD | = 18 ∘ .