Wyznacz zbiór wartości funkcji określonej wzorem: 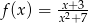 dla
dla 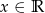 .
.
/Szkoła średnia/Funkcje/Wymierna/Zbiór wartości
Wyznacz wartość największą i najmniejszą funkcji 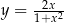 w przedziale
w przedziale 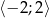 .
.
Dana jest funkcja 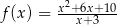 .
.
- Określ przedziały monotoniczności tej funkcji.
- Znajdź ekstrema lokalne funkcji
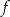 .
.
Funkcja 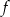 określona jest wzorem
określona jest wzorem 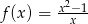 .
.
- Wykaż ze zbiorem wartości funkcji
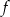 jest zbiór liczb rzeczywistych.
jest zbiór liczb rzeczywistych. - Uzasadnij, że funkcja
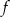 nie jest rożnowartościowa.
nie jest rożnowartościowa.
Dana jest funkcja 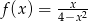 , gdzie
, gdzie 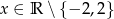 . Wykaż, że zbiorem wartości tej funkcji jest zbiór liczb rzeczywistych.
. Wykaż, że zbiorem wartości tej funkcji jest zbiór liczb rzeczywistych.
Uzasadnij, że funkcja 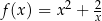 przyjmuje dla dodatnich argumentów wartości nie mniejsze niż 3.
przyjmuje dla dodatnich argumentów wartości nie mniejsze niż 3.
Wykaż, że dla każdej liczby rzeczywistej dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność
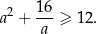
Wykaż, że dla każdej liczby rzeczywistej dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność
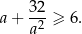
Uzasadnij, że dla każdej liczby dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność 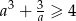 .
.
Wyznacz największą wartość funkcji 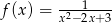 .
.
Wyznacz przedziały monotoniczności i ekstrema lokalne funkcji 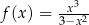 .
.
Liczby rzeczywiste  i
i  spełniają warunek
spełniają warunek 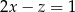 . Wyznacz takie wartości
. Wyznacz takie wartości  i
i  , dla których wyrażenie
, dla których wyrażenie 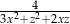 przyjmuje największą wartość. Podaj tę największą wartość.
przyjmuje największą wartość. Podaj tę największą wartość.
Funkcja 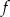 określona jest wzorem
określona jest wzorem 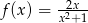 .
.
- Wykaż, że funkcja
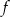 jest nieparzysta.
jest nieparzysta. - Wykaż, że zbiór wartości funkcji
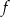 zawiera się w zbiorze
zawiera się w zbiorze 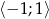 .
.

