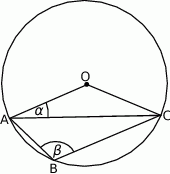
Udowodnij, że jeżeli  jest środkiem okręgu, na którym leżą punkty
jest środkiem okręgu, na którym leżą punkty  , to
, to  .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Udowodnij, że jeżeli  jest środkiem okręgu, na którym leżą punkty
jest środkiem okręgu, na którym leżą punkty  , to
, to  .
.

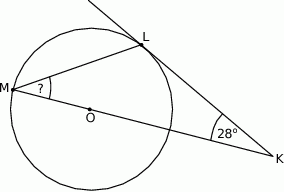
Dany jest okrąg o środku w punkcie 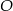 . Prosta
. Prosta 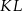 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 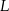 , a środek
, a środek 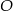 tego okręgu leży na odcinku
tego okręgu leży na odcinku 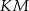 (zob. rysunek). Udowodnij, że kąt
(zob. rysunek). Udowodnij, że kąt 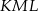 ma miarę
ma miarę 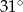 .
.
Okrąg dopisany do boku 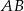 trójkąta
trójkąta 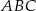 to okrąg, który jest jednocześnie styczny do tego boku, oraz do przedłużeń boków
to okrąg, który jest jednocześnie styczny do tego boku, oraz do przedłużeń boków 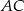 i
i 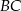 .
.
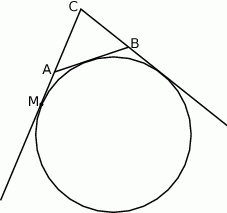
Wykaż, że jeżeli 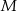 jest punktem styczności tego okręgu z przedłużeniem boku
jest punktem styczności tego okręgu z przedłużeniem boku 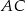 to długość odcinka
to długość odcinka  jest równa połowie obwodu trójkąta
jest równa połowie obwodu trójkąta 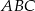 .
.
Wykaż, że stosunek pola kwadratu wpisanego w koło do pola tego koła jest mniejszy od  .
.
Wykaż, że stosunek pola kwadratu opisanego na kole do pola tego koła jest mniejszy od 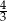 .
.
Na okręgu o promieniu  wybrano punkty
wybrano punkty 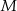 i
i 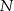 w ten sposób, że proste
w ten sposób, że proste 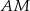 i
i 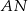 są styczne do okręgu. Punkt
są styczne do okręgu. Punkt 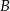 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 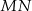 i prostej łączącej
i prostej łączącej 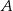 ze środkiem
ze środkiem 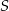 tego okręgu. Wykaż, że
tego okręgu. Wykaż, że 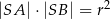 .
.
Z półokręgów budujemy krzywą (patrz rysunek). Pierwszy półokrąg ma promień długości 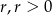 , a promień każdego następnego półokręgu stanowi
, a promień każdego następnego półokręgu stanowi  promienia poprzedniego. Niech
promienia poprzedniego. Niech  oznacza liczbę półokręgów tworzących tę krzywą. Udowodnij, że dla dowolnej liczby naturalnej dodatniej
oznacza liczbę półokręgów tworzących tę krzywą. Udowodnij, że dla dowolnej liczby naturalnej dodatniej  długość krzywej jest mniejsza od
długość krzywej jest mniejsza od 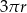 .
.

Na okręgu o środku 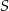 wybrano punkty
wybrano punkty 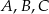 i
i 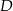 w ten sposób, że prosta
w ten sposób, że prosta 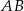 zawiera punkt
zawiera punkt 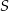 , a proste
, a proste 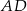 i
i 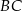 przecinają się w punkcie
przecinają się w punkcie 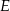 . Punkt
. Punkt 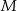 jest punktem wspólnym prostych
jest punktem wspólnym prostych 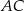 i
i 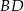 . Wykaż, że proste
. Wykaż, że proste 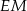 i
i 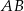 są prostopadłe.
są prostopadłe.
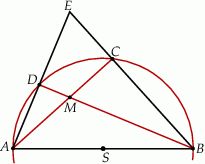
Na okręgu wybrano takich pięć różnych punktów: 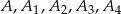 , że
, że
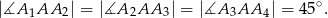
Udowodnij, że punkty 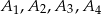 są wierzchołkami kwadratu.
są wierzchołkami kwadratu.
Dany jest okrąg 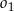 . Kreślimy cięciwę
. Kreślimy cięciwę 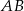 nieprzechodzącą przez środek okręgu
nieprzechodzącą przez środek okręgu 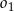 , a następnie rysujemy okrąg
, a następnie rysujemy okrąg 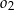 współśrodkowy z okręgiem
współśrodkowy z okręgiem 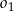 i styczny do cięciwy
i styczny do cięciwy 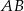 . Okręgi
. Okręgi 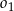 i
i 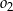 ograniczają pierścień kołowy. Uzasadnij, że pole pierścienia kołowego nie zależy od długości promienia okręgu
ograniczają pierścień kołowy. Uzasadnij, że pole pierścienia kołowego nie zależy od długości promienia okręgu 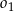 (zależy tylko od długości cięciwy
(zależy tylko od długości cięciwy 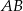 ).
).
W pierścieniu kołowym cięciwa zewnętrznego okręgu ma długość 10 i jest styczna do wewnętrznego okręgu (zobacz rysunek).
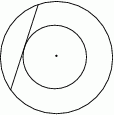
Wykaż, że pole tego pierścienia można wyrazić wzorem, w którym nie występują promienie wyznaczających go okręgów.
Dany jest okrąg 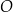 . Przez punkt
. Przez punkt 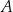 poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio –
poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – 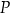 oraz
oraz 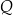 . Przez punkt
. Przez punkt 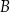 leżący na odcinku
leżący na odcinku 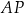 poprowadzono styczną do tego okręgu w punkcie
poprowadzono styczną do tego okręgu w punkcie  , która przecięła odcinek
, która przecięła odcinek  w punkcie
w punkcie  (zobacz rysunek).
(zobacz rysunek).
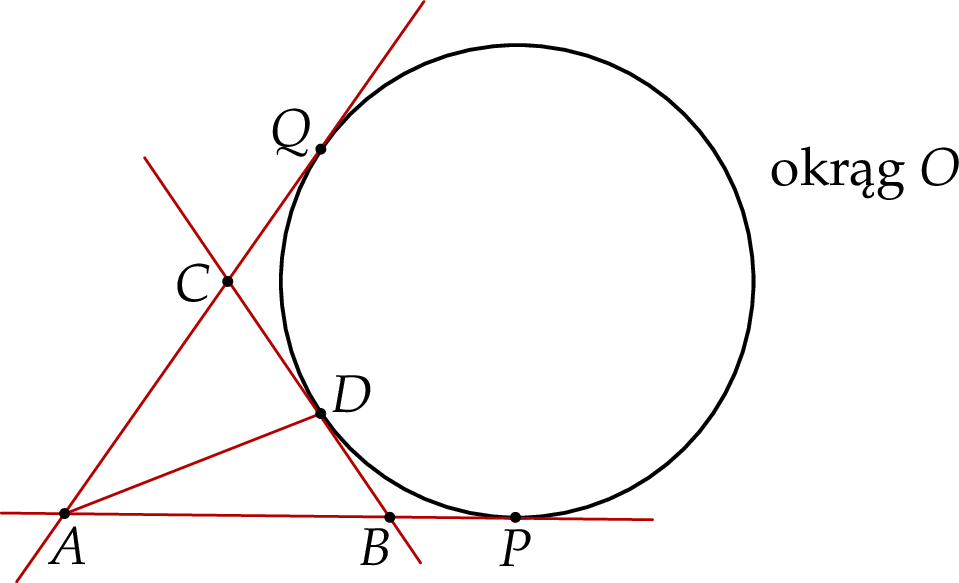
Wykaż, że jeżeli 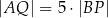 oraz
oraz 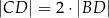 , to trójkąt
, to trójkąt 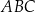 jest równoramienny.
jest równoramienny.
Dany jest okrąg 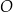 . Przez punkt
. Przez punkt 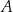 poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio –
poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – 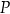 oraz
oraz 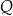 . Przez punkt
. Przez punkt 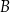 leżący na odcinku
leżący na odcinku 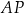 poprowadzono styczną do tego okręgu w punkcie
poprowadzono styczną do tego okręgu w punkcie 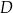 , która przecięła odcinek
, która przecięła odcinek  w punkcie
w punkcie  (zobacz rysunek).
(zobacz rysunek).
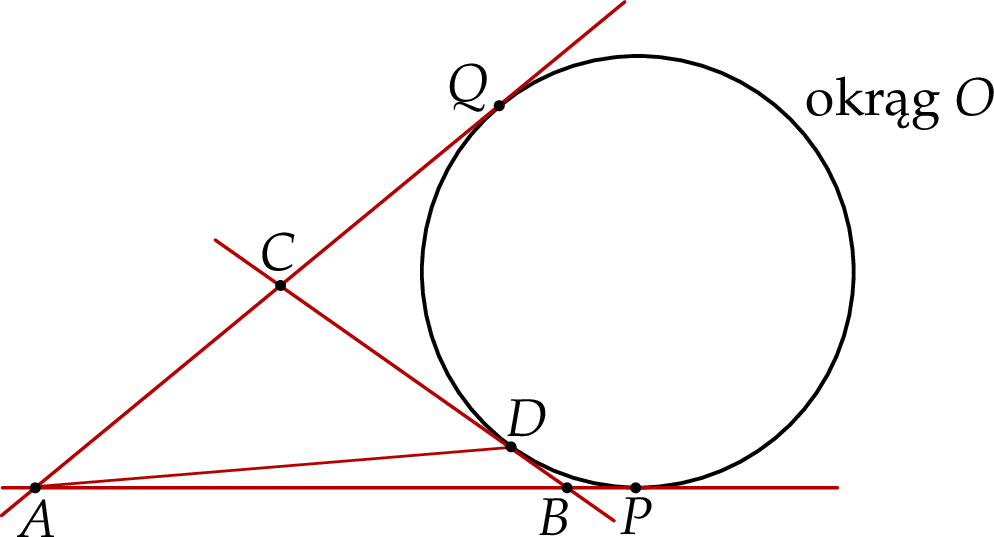
Wykaż, że jeżeli 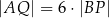 oraz
oraz 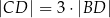 , to trójkąt
, to trójkąt 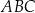 nie jest równoramienny.
nie jest równoramienny.
Przez punkt styczności dwóch okręgów poprowadzono sieczną. Udowodnij, że wypukłe kąty środkowe oparte na łukach wyznaczonych przez tę sieczną na okręgach mają równe miary.
Dwa okręgi są styczne zewnętrznie w punkcie 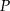 . Poprowadzono prostą, styczną do obu okręgów odpowiednio w punktach
. Poprowadzono prostą, styczną do obu okręgów odpowiednio w punktach 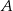 i
i 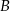 (
(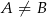 ). Wykaż, że kąt
). Wykaż, że kąt 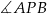 jest prosty.
jest prosty.
Dwa okręgi są zewnętrznie styczne w punkcie 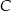 oraz są styczne do prostej
oraz są styczne do prostej 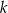 w punktach
w punktach 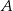 i
i 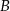 odpowiednio (zobacz rysunek).
odpowiednio (zobacz rysunek).
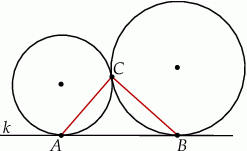
Uzasadnij, że trójkąt  jest prostokątny.
jest prostokątny.
Trójkąt  jest trójkątem równobocznym o boku długości
jest trójkątem równobocznym o boku długości  . Wykaż, że łuk okręgu opisanego na tym trójkącie zawarty między wierzchołkami
. Wykaż, że łuk okręgu opisanego na tym trójkącie zawarty między wierzchołkami  i
i 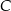 ma długość większą niż
ma długość większą niż 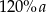 .
.
Trójkąt 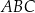 jest trójkątem równobocznym o boku długości
jest trójkątem równobocznym o boku długości  . Wykaż, że łuk okręgu wpisanego w ten trójkąt zawarty między dwoma kolejnymi punktami styczności tego okręgu z bokami trójkąta ma długość większą niż
. Wykaż, że łuk okręgu wpisanego w ten trójkąt zawarty między dwoma kolejnymi punktami styczności tego okręgu z bokami trójkąta ma długość większą niż 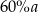 .
.

W danym okręgu o środku 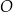 poprowadzono cięciwy
poprowadzono cięciwy 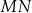 i
i 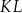 , które przecięły się w punkcie
, które przecięły się w punkcie 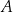 .
.

Wykaż, że trójkąty 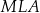 i
i 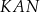 są podobne.
są podobne.
Wiedząc, że 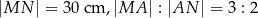 oraz
oraz 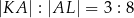 , oblicz długość cięciwy
, oblicz długość cięciwy 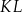 .
.
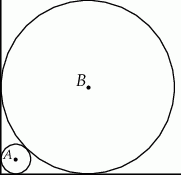
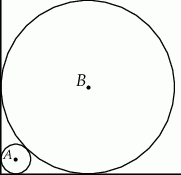
Dwa okręgi o środkach 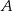 i
i 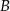 są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek promienia większego z tych okręgów do promienia mniejszego jest równy
są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek promienia większego z tych okręgów do promienia mniejszego jest równy 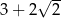 .
.
Dwa okręgi o środkach  i
i  są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek obwodu większego z tych okręgów do obwodu mniejszego jest równy
są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek obwodu większego z tych okręgów do obwodu mniejszego jest równy 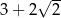 .
.
Do dwóch okręgów przecinających się w punktach  i
i  poprowadzono wspólną styczną
poprowadzono wspólną styczną 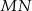 , przy czym punkt
, przy czym punkt 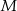 należy do pierwszego, a punkt
należy do pierwszego, a punkt 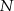 do drugiego okręgu. Wykaż, że prosta
do drugiego okręgu. Wykaż, że prosta 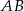 dzieli odcinek
dzieli odcinek 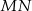 na połowy.
na połowy.
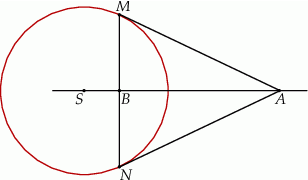
Średnica 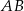 i cięciwa
i cięciwa 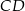 okręgu o środku
okręgu o środku 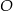 i promieniu
i promieniu  przecinają się w punkcie
przecinają się w punkcie 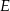 takim, że
takim, że 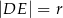 . Wykaż, że
. Wykaż, że 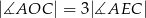 .
.
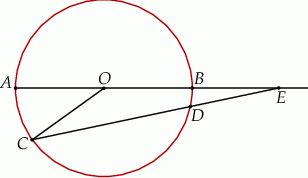
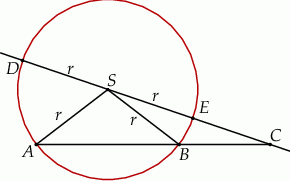
Dany jest okrąg o środku w punkcie 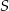 i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy 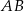 poza punkt
poza punkt 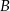 odłożono odcinek
odłożono odcinek 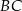 równy promieniowi danego okręgu. Przez punkty
równy promieniowi danego okręgu. Przez punkty 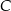 i
i 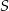 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 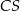 przecina dany okrąg w punktach
przecina dany okrąg w punktach 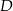 i
i 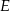 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 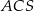 jest równa
jest równa  , to miara kąta
, to miara kąta 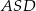 jest równa
jest równa 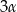 .
.