Zadania.info Największy internetowy zbiór zadań z matematyki

/Studia/Algebra liniowa/Odwzorowania liniowe

Wyszukiwanie zadań

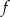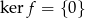Wykazać, że na to aby odwzorowanie f było różnowartościowe potrzeba i wystarcza, aby ke rf = { 0} .

Wykazać, że jeśli 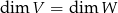dim V = d im W , to z tego, że odwzorowanie liniowe 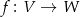f : V → W jest różnowartościowe wynika, że 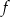f jest izomorfizmem.

Wykazać, że jeśli 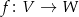f : V → W jest odwzorowaniem liniowym, to f(0) = 0 .

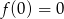Które z następujących odwzorowań są liniowe:

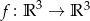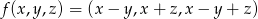
  • f : R 3 → R 3 , f (x,y,z) = (x − y ,x + z,x− y+ z)
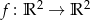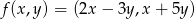
  • f : R 2 → R 2 , f (x,y) = (2x − 3y ,x+ 5y)
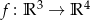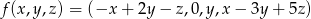
  • f : R 3 → R 4 , f (x,y,z) = (−x + 2y − z,0 ,y ,x− 3y+ 5z)
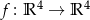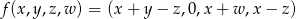
  • 4 4 f : R → R , f (x,y,z,w ) = (x + y − z,0,x + w ,x − z)
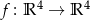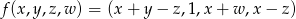
  • f : R 4 → R 4 , f (x,y,z,w ) = (x + y − z,1,x + w ,x − z)
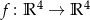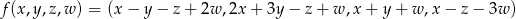
  • f : R 4 → R 4 , f (x,y,z,w ) = (x− y− z+ 2w ,2x + 3y− z+ w,x + y + w ,x − z − 3w )
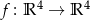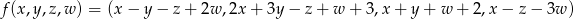
  • f : R 4 → R 4 , f (x,y,z,w ) = (x− y− z+ 2w ,2x + 3y− z+ w + 3,x + y + w + 2,x − z − 3w )

Załóżmy, że odwzorowanie liniowe 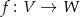f : V → W jest różnowartościowe.

  • Wykazać, że 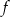f przekształca układ wektorów liniowo niezależnych w 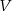V na układ wektorów liniowo niezależnych w W .
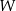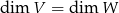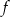  • Wykazać, że jeśli d im V = dim W to f przekształca bazę w 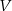V na bazę w W .

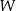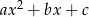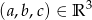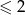Wykazać, że funkcja przyporządkowująca wielomianowi 2 ax + bx + c wektor (a,b,c) ∈ R 3 jest izomorfizmem przestrzeni R [x]2 wielomianów stopnia ≤ 2 i przestrzeni R 3 .

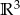Wykazać, że relacja izomorfizmu jest relacją równoważności w zbiorze przestrzeni liniowych.

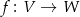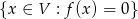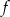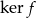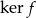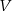Niech f : V → W będzie odwzorowaniem liniowym. Zbiór {x ∈ V : f (x) = 0} nazywa się jądrem odwzorowania f i oznacza się symbolem ker f . Wykazać, że k erf jest podprzestrzenią przestrzeni V .