Wykaż, że jeżeli 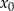 jest rozwiązaniem równania
jest rozwiązaniem równania 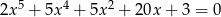 , to
, to 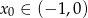 .
.
/Szkoła średnia/Równania/Wielomianowe/Stopnia 5
Rozwiąż równanie 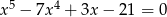 .
.
Ukryj
Podobne zadania
Rozwiąż równanie 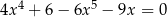 .
.
Dla jakich wartości parametru 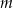 równanie
równanie 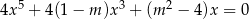 ma dokładnie trzy różne rozwiązania?
ma dokładnie trzy różne rozwiązania?
Rozwiąż równanie 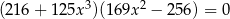 .
.
Rozwiąż równanie
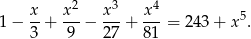
Dla jakich wartości parametru 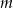 równanie
równanie 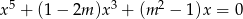 ma
ma
- pięć pierwiastków;
- dokładnie 3 pierwiastki;
- tylko jeden pierwiastek?
Wyznacz wszystkie całkowite wartości parametru 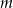 , dla których równanie
, dla których równanie
![3 2 [ 2 2 ] (x + 2x + 2x + 1 ) x − (2m + 1)x + m + m = 0](https://img.zadania.info/zad/5455135/HzadT1x.gif)
ma trzy, parami różne, pierwiastki rzeczywiste, takie że jeden z nich jest średnią arytmetyczną dwóch pozostałych.
Uzasadnij, że wielomian 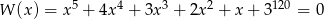 nie ma pierwiastków wymiernych.
nie ma pierwiastków wymiernych.
Rozwiąż równanie 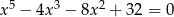 .
.
Ukryj
Podobne zadania
Rozwiąż równanie 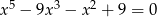 .
.
Rozwiąż równanie 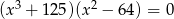 .
.
Ukryj
Podobne zadania
Rozwiąż równanie 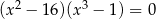 .
.
Rozwiąż równanie 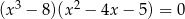 .
.
Rozwiąż równanie 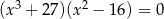 .
.
Rozwiąż równanie 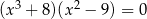 .
.
Rozwiąż równanie 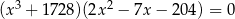 .
.
Rozwiąż równanie 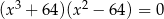 .
.
Rozwiąż równanie 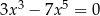 .
.
Dla jakich wartości parametru 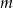 równanie
równanie ![3 2 2 (x + 3x − 4)[(m − 5 )x + (m − 2)x − 1 ] = 0](https://img.zadania.info/zad/9801521/HzadT1x.gif) ma cztery różne pierwiastki?
ma cztery różne pierwiastki?

