Ze zbioru 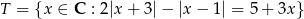 losujemy 3 liczby
losujemy 3 liczby 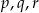 ze zwracaniem i tworzymy funkcję
ze zwracaniem i tworzymy funkcję 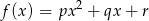 . Oblicz prawdopodobieństwa zdarzeń:
. Oblicz prawdopodobieństwa zdarzeń:
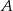 – otrzymana funkcja jest parzysta.
– otrzymana funkcja jest parzysta. 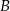 – otrzymana funkcja jest różnowartościowa.
– otrzymana funkcja jest różnowartościowa. 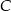 – otrzymana funkcja jest stała.
– otrzymana funkcja jest stała.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Ze zbioru 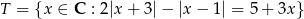 losujemy 3 liczby
losujemy 3 liczby 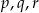 ze zwracaniem i tworzymy funkcję
ze zwracaniem i tworzymy funkcję 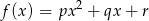 . Oblicz prawdopodobieństwa zdarzeń:
. Oblicz prawdopodobieństwa zdarzeń:
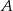 – otrzymana funkcja jest parzysta.
– otrzymana funkcja jest parzysta. 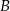 – otrzymana funkcja jest różnowartościowa.
– otrzymana funkcja jest różnowartościowa. 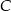 – otrzymana funkcja jest stała.
– otrzymana funkcja jest stała.Ze zbioru 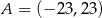 losujemy dwucyfrową liczbę całkowitą
losujemy dwucyfrową liczbę całkowitą  , natomiast ze zbioru
, natomiast ze zbioru 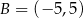 losujemy liczbę całkowitą
losujemy liczbę całkowitą 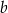 . Te liczby są współczynnikami funkcji
. Te liczby są współczynnikami funkcji 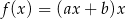 . Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wykres otrzymanej funkcji
. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wykres otrzymanej funkcji 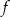 ma co najmniej dwa punkty wspólne z prostą
ma co najmniej dwa punkty wspólne z prostą 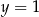 .
.
Wzór funkcji 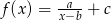 tworzymy w następujący sposób. Ze zbioru
tworzymy w następujący sposób. Ze zbioru
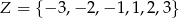
losujemy kolejno 3 liczby (bez zwracania); pierwsza z wylosowanych liczb jest równa współczynnikowi  , druga – współczynnikowi
, druga – współczynnikowi 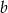 , trzecia – współczynnikowi
, trzecia – współczynnikowi  . Oblicz prawdopodobieństwo zdarzeń:
. Oblicz prawdopodobieństwo zdarzeń:
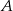 – funkcja
– funkcja 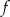 jest funkcją malejącą w każdym ze zbiorów
jest funkcją malejącą w każdym ze zbiorów 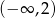 oraz
oraz 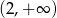 ;
; 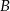 – miejscem zerowym funkcji
– miejscem zerowym funkcji 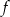 jest 0.
jest 0. 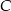 – funkcja
– funkcja 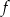 jest funkcją malejącą w każdym ze zbiorów
jest funkcją malejącą w każdym ze zbiorów 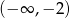 oraz
oraz 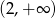 ;
;Ze zbioru 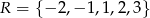 losujemy najpierw jedną liczbę i oznaczamy ją jako
losujemy najpierw jedną liczbę i oznaczamy ją jako  . Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako
. Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako 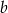 . Liczby
. Liczby  i
i 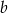 są współczynnikami funkcji kwadratowej
są współczynnikami funkcji kwadratowej 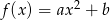 . Oblicz prawdopodobieństwo zdarzenia:
. Oblicz prawdopodobieństwo zdarzenia:
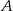 – funkcja
– funkcja 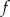 jest malejąca w zbiorze
jest malejąca w zbiorze 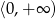 ,
, 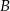 – funkcja
– funkcja 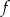 ma dwa różne miejsca zerowe.
ma dwa różne miejsca zerowe.Ze zbioru 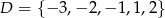 losujemy najpierw jedną liczbę i oznaczamy ją jako
losujemy najpierw jedną liczbę i oznaczamy ją jako  . Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako
. Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako 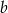 . Liczby
. Liczby  i
i 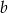 są współczynnikami funkcji kwadratowej
są współczynnikami funkcji kwadratowej 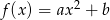 . Oblicz prawdopodobieństwo zdarzenia:
. Oblicz prawdopodobieństwo zdarzenia:
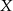 – funkcja
– funkcja 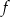 jest malejąca w zbiorze
jest malejąca w zbiorze 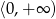 ,
, 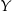 – funkcja
– funkcja 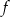 ma dwa różne miejsca zerowe.
ma dwa różne miejsca zerowe.Niech 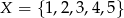 i
i 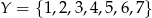 . Oblicz prawdopodobieństwo, że zbiór wartości losowo utworzonej funkcji
. Oblicz prawdopodobieństwo, że zbiór wartości losowo utworzonej funkcji 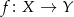 jest dwuelementowy.
jest dwuelementowy.
Losujemy dwie różne liczby całkowite  i
i 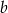 z przedziału
z przedziału 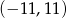 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 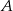 – równanie
– równanie 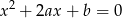 nie ma rozwiązań.
nie ma rozwiązań.
Ze zbioru 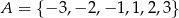 losujemy liczbę
losujemy liczbę  , natomiast ze zbioru
, natomiast ze zbioru 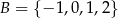 losujemy liczbę
losujemy liczbę 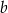 . Te liczby są – odpowiednio – współczynnikiem kierunkowym i wyrazem wolnym funkcji liniowej
. Te liczby są – odpowiednio – współczynnikiem kierunkowym i wyrazem wolnym funkcji liniowej 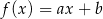 . Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymana funkcja
. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymana funkcja 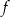 jest rosnąca i ma dodatnie miejsce zerowe.
jest rosnąca i ma dodatnie miejsce zerowe.
Ze zbioru 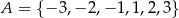 losujemy liczbę
losujemy liczbę  , natomiast ze zbioru
, natomiast ze zbioru 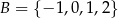 losujemy liczbę
losujemy liczbę 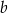 . Te liczby są – odpowiednio – współczynnikiem kierunkowym i wyrazem wolnym funkcji liniowej
. Te liczby są – odpowiednio – współczynnikiem kierunkowym i wyrazem wolnym funkcji liniowej 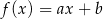 . Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymana funkcja
. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymana funkcja 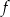 jest malejąca i ma dodatnie miejsce zerowe.
jest malejąca i ma dodatnie miejsce zerowe.
Ze zbioru 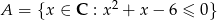 losujemy 2 liczby
losujemy 2 liczby  i
i 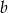 bez zwracania i tworzymy funkcję
bez zwracania i tworzymy funkcję 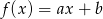 . Oblicz prawdopodobieństwo otrzymania funkcji malejącej.
. Oblicz prawdopodobieństwo otrzymania funkcji malejącej.
Ze zbioru 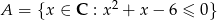 losujemy 2 liczby
losujemy 2 liczby  i
i 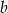 bez zwracania i tworzymy funkcję
bez zwracania i tworzymy funkcję 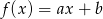 . Oblicz prawdopodobieństwo otrzymania funkcji, która nie ma miejsc zerowych.
. Oblicz prawdopodobieństwo otrzymania funkcji, która nie ma miejsc zerowych.
