Dany jest trójkąt równoramienny o bokach długości 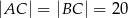 i
i 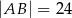 . Odcinek
. Odcinek 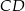 jest wysokością trójkąta
jest wysokością trójkąta 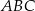 , a odcinek
, a odcinek 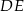 jest wysokością trójkąta
jest wysokością trójkąta 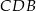 (zobacz rysunek).
(zobacz rysunek).
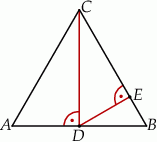
Oblicz długość odcinka 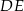 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest trójkąt równoramienny o bokach długości 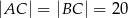 i
i 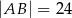 . Odcinek
. Odcinek 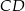 jest wysokością trójkąta
jest wysokością trójkąta 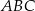 , a odcinek
, a odcinek 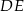 jest wysokością trójkąta
jest wysokością trójkąta 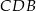 (zobacz rysunek).
(zobacz rysunek).

Oblicz długość odcinka 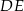 .
.
Dwa spośród boków trójkąta równoramiennego mają długości 3 cm i 4 cm. Jaką długość może mieć trzeci bok?
Dwa spośród boków trójkąta równoramiennego mają długości 2 cm i 5 cm. Jaką długość może mieć trzeci bok?
Dwa spośród boków trójkąta równoramiennego mają długości 5 cm i 11 cm. Jaką długość może mieć trzeci bok?
Dwa spośród boków trójkąta równoramiennego mają długości 5 cm i 9 cm. Jaką długość może mieć trzeci bok?
Liczby 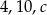 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Liczby 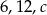 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
Liczby 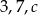 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
W trójkącie równoramiennym wysokość poprowadzona do podstawy ma długość 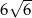 . Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.
. Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.
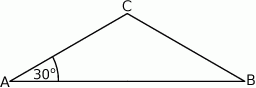
Kąt przy podstawie trójkąta równoramiennego 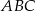 ma miarę
ma miarę 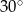 . Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta
. Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta 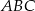 .
.
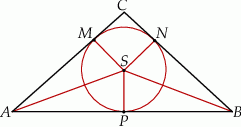
W trójkąt równoramienny 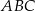 (
(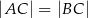 ) wpisano okrąg o środku
) wpisano okrąg o środku 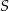 . Punkty wspólne okręgu i trójkąta oznaczono literami
. Punkty wspólne okręgu i trójkąta oznaczono literami 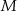 ,
, 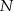 i
i 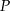 . Uzasadnij, że trójkąty
. Uzasadnij, że trójkąty 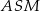 i
i 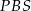 są przystające.
są przystające.
Dany jest trójkąt ostrokątny równoramienny 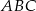 , w którym bok
, w którym bok 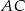 jest równy
jest równy 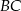 . Odcinek
. Odcinek 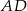 jest wysokością tego trójkąta, oraz odcinek
jest wysokością tego trójkąta, oraz odcinek 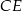 jest wysokością tego trójkąta. Udowodnij, że kąt
jest wysokością tego trójkąta. Udowodnij, że kąt 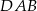 jest równy kątowi
jest równy kątowi 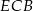 .
.
Liczby 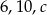 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Jaka jest miara kąta  ?
?
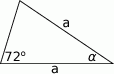
Jaka jest miara kąta  ?
?
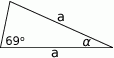
Jaka jest miara kąta  ?
?
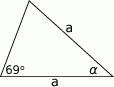
Udowodnij, że w trójkącie równoramiennym wysokości poprowadzone do równych boków są równej długości.
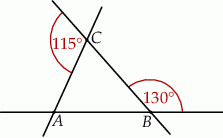
Trzy proste przecinające się w sposób przedstawiony na rysunku tworzą trójkąt 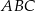 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt  jest równoramienny.
jest równoramienny.
Oblicz pole trójkąta równoramiennego 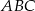 , w którym
, w którym 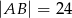 i
i 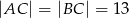 .
.
Udowodnij, że w trójkącie równoramiennym środkowe poprowadzone do równych boków są równej długości.
Odcinek 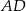 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 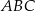 , w którym
, w którym 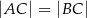 . Udowodnij, że
. Udowodnij, że 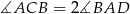 .
.
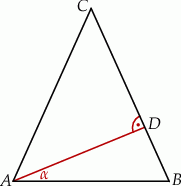
Wykaż, że miara kąta między wysokością trójkąta równoramiennego poprowadzoną do ramienia a podstawą tego trójkąta jest dwa razy mniejsza od miary kąta zawartego między ramionami tego trójkąta.
Liczby 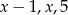 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
