Podstawą ostrosłupa 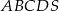 jest kwadrat
jest kwadrat 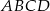 . Trójkąt równoramienny
. Trójkąt równoramienny 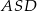 ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź
ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź 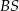 ma długość 17. Oblicz pole przekroju ostrosłupa płaszczyzną
ma długość 17. Oblicz pole przekroju ostrosłupa płaszczyzną 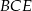 , gdzie
, gdzie 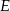 jest środkiem krawędzi
jest środkiem krawędzi 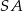 .
.
/Szkoła średnia/Geometria
W pojemniku o kształcie walca o promieniu podstawy 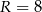 umieszczono dwie kule o promieniu
umieszczono dwie kule o promieniu 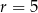 , w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.
, w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.
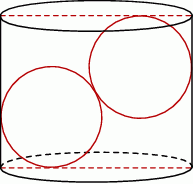
Objętość stożka ściętego (przedstawionego na rysunku) można obliczyć ze wzoru 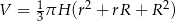 , gdzie
, gdzie  i
i 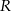 są promieniami podstaw (
są promieniami podstaw (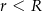 ), a
), a 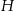 jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa 10, objętość
jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa 10, objętość 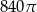 , a
, a 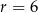 . Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.
. Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.
We wnętrzu sześcianu umieszczono czworościan foremny w ten sposób, że wszystkie krawędzie czworościanu są przekątnymi ścian bocznych sześcianu. Wyznacz stosunek objętości czworościanu do objętości sześcianu.
Koło 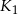 ma promień długości
ma promień długości  . Wewnątrz tego koła rysujemy kolejno koła
. Wewnątrz tego koła rysujemy kolejno koła 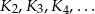 takie, że kolejne koło ma średnicę równą promieniowi poprzedniego koła.
takie, że kolejne koło ma średnicę równą promieniowi poprzedniego koła.
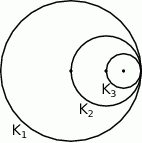
Wyznacz pole koła 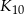 .
.
Pole równoległoboku 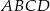 o danych wierzchołkach
o danych wierzchołkach 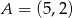 i
i 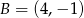 jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej
jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej 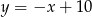 , który ma obie współrzędne będące liczbami całkowitymi.
, który ma obie współrzędne będące liczbami całkowitymi.
Oblicz pole ośmiokąta foremnego wpisanego w okrąg o promieniu 6.
W trójkącie 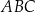 kąt
kąt 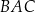 jest dwa razy większy od kąta
jest dwa razy większy od kąta 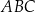 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość 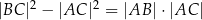 .
.
Dany jest trójkąt 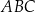 , który nie jest równoramienny. W tym trójkącie miara kąta
, który nie jest równoramienny. W tym trójkącie miara kąta 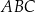 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 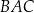 . Wykaż, że długości boków tego trójkąta spełniają warunek
. Wykaż, że długości boków tego trójkąta spełniają warunek
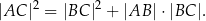
Okrąg  jest styczny do boków
jest styczny do boków 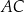 i
i 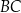 trójkąta
trójkąta 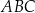 oraz przecina bok
oraz przecina bok 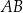 tego trójkąta w punktach
tego trójkąta w punktach 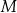 oraz
oraz 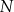 , przy czym
, przy czym 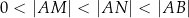 . Wykaż, że jeśli
. Wykaż, że jeśli 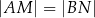 , to trójkąt
, to trójkąt 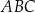 jest równoramienny.
jest równoramienny.
Dane są wektory: ![→ u = [2;− 4]](https://img.zadania.info/zad/9899559/HzadT0x.gif) ,
, ![→ v = [− 3;5]](https://img.zadania.info/zad/9899559/HzadT1x.gif) . Oblicz
. Oblicz 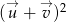 .
.
Dane są wektory: ![→ u = [2;− 4]](https://img.zadania.info/zad/2354795/HzadT0x.gif) ,
, ![→ v = [− 3;5]](https://img.zadania.info/zad/2354795/HzadT1x.gif) . Oblicz
. Oblicz 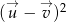 .
.
Dane są wektory: ![→ u = [2;− 4]](https://img.zadania.info/zad/7943696/HzadT0x.gif) ,
, ![→ v = [− 3;5]](https://img.zadania.info/zad/7943696/HzadT1x.gif) . Oblicz
. Oblicz 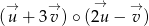 .
.
Średnica 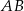 i cięciwa
i cięciwa 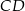 okręgu o środku
okręgu o środku 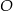 i promieniu
i promieniu  przecinają się w punkcie
przecinają się w punkcie 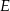 takim, że
takim, że 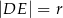 . Wykaż, że
. Wykaż, że 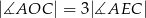 .
.
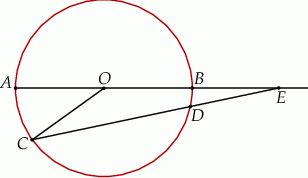
Dany jest okrąg o środku w punkcie 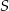 i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy 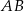 poza punkt
poza punkt 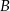 odłożono odcinek
odłożono odcinek 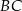 równy promieniowi danego okręgu. Przez punkty
równy promieniowi danego okręgu. Przez punkty 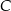 i
i 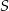 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 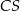 przecina dany okrąg w punktach
przecina dany okrąg w punktach 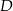 i
i 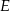 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 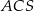 jest równa
jest równa  , to miara kąta
, to miara kąta 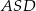 jest równa
jest równa 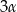 .
.
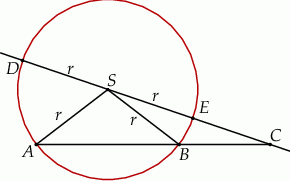
Trójkąt 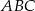 przedstawiony na poniższym rysunku jest równoboczny, a punkty
przedstawiony na poniższym rysunku jest równoboczny, a punkty 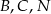 są współliniowe. Na boku
są współliniowe. Na boku 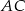 wybrano punkt
wybrano punkt 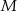 tak, że
tak, że 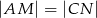 . Wykaż, że
. Wykaż, że 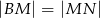 .
.
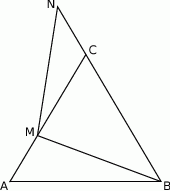
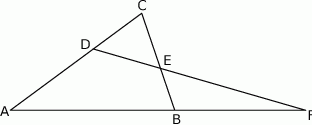
Dany jest trójkąt 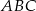 , w którym
, w którym 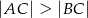 . Na bokach
. Na bokach 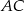 i
i 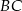 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 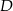 i
i 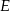 , że
, że 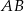 i
i 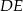 przecinają się w punkcie
przecinają się w punkcie 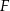 (zobacz rysunek). Wykaż, że jeżeli
(zobacz rysunek). Wykaż, że jeżeli 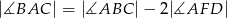 , to
, to 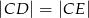 .
.
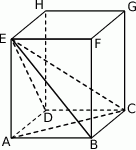
W graniastosłupie prawidłowym czworokątnym 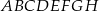 przekątna
przekątna 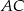 podstawy ma długość 4. Kąt
podstawy ma długość 4. Kąt 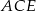 jest równy
jest równy 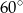 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa  przedstawionego na poniższym rysunku.
przedstawionego na poniższym rysunku.
Dany jest okrąg o promieniu 11 oraz punkt 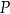 oddalony o 7 od środka okręgu. Przez punkt
oddalony o 7 od środka okręgu. Przez punkt 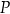 poprowadzono cięciwę o długości 18. W jakim stosunku punkt
poprowadzono cięciwę o długości 18. W jakim stosunku punkt 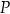 podzielił tę cięciwę na dwa odcinki?
podzielił tę cięciwę na dwa odcinki?
Przyprostokątne trójkąta prostokątnego 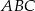 mają długości 12 i 6. Oblicz długość promienia okręgu stycznego do obu przyprostokątnych, którego środek
mają długości 12 i 6. Oblicz długość promienia okręgu stycznego do obu przyprostokątnych, którego środek 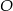 leży na przeciwprostokątnej, oraz oblicz odległości środka
leży na przeciwprostokątnej, oraz oblicz odległości środka 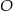 od wierzchołków trójkąta
od wierzchołków trójkąta 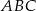 .
.
W układzie współrzędnych dane są dwa punkty: 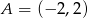 i
i 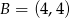 .
.
- Wyznacz równanie symetralnej odcinka
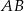 .
. - Prosta
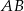 oraz prosta o równaniu
oraz prosta o równaniu 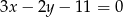 przecinają się w punkcie
przecinają się w punkcie 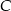 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 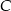 .
.
Jaki warunek musi spełniać liczba  , aby istniał trójkąt o bokach
, aby istniał trójkąt o bokach 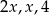 ?
?
Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu 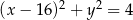 jest okrąg o równaniu
jest okrąg o równaniu 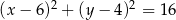 , a skala tej jednokładności jest liczbą ujemną.
, a skala tej jednokładności jest liczbą ujemną.
Dany jest ostrosłup prawidłowy sześciokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 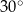 i ma długość równą 6 (zobacz rysunek).
i ma długość równą 6 (zobacz rysunek).
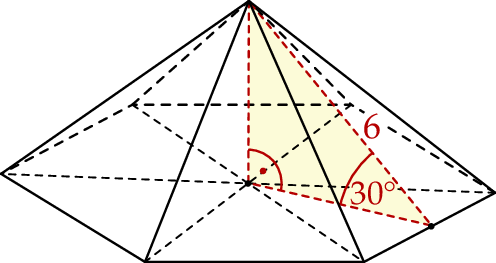
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

