Ostrokątny trójkąt równoramienny 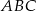 o podstawie
o podstawie 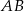 jest wpisany w okrąg o równaniu
jest wpisany w okrąg o równaniu 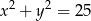 . Punkty
. Punkty 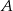 i
i 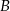 leżą na prostej o równaniu
leżą na prostej o równaniu 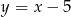 .
.
- Oblicz współrzędne punktów:
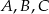 .
. - Oblicz kąty trójkąta
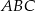 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Ostrokątny trójkąt równoramienny 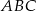 o podstawie
o podstawie 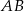 jest wpisany w okrąg o równaniu
jest wpisany w okrąg o równaniu 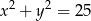 . Punkty
. Punkty 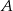 i
i 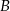 leżą na prostej o równaniu
leżą na prostej o równaniu 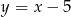 .
.
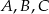 .
. 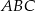 .
.W sześciokącie foremnym połączono środki sąsiednich boków otrzymując ponownie sześciokąt foremny. Oblicz stosunek pól: otrzymanego i wyjściowego sześciokąta.
Dany jest trójkąt równoboczny 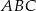 . Okrąg o średnicy
. Okrąg o średnicy 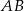 przecina bok
przecina bok 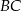 w punkcie
w punkcie 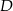 .
.
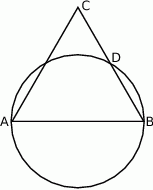
Wykaż, że 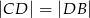 .
.
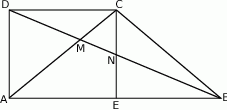
Punkt 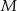 jest punktem wspólnym przekątnych trapezu prostokątnego
jest punktem wspólnym przekątnych trapezu prostokątnego 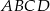 . Punkt
. Punkt 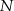 jest punktem wspólnym przekątnej
jest punktem wspólnym przekątnej 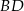 i wysokości
i wysokości 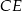 opuszczonej na dłuższą podstawę
opuszczonej na dłuższą podstawę 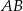 . Wykaż, że
. Wykaż, że 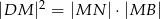 .
.
Udowodnij, że trzy środkowe rozcinają trójkąt na sześć części o równych polach.
Odcinki 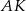 i
i 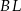 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 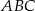 , a punkt
, a punkt 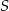 punktem ich przecięcia. Wykaż, że podobne są trójkąty:
punktem ich przecięcia. Wykaż, że podobne są trójkąty:
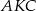 i
i 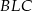 ;
; 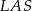 i
i 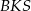 ;
; 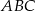 i
i 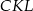 .
.Odcinki 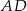 i
i 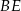 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 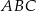 , a punkt
, a punkt 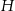 jest punktem ich przecięcia. Uzasadnij, że punkty
jest punktem ich przecięcia. Uzasadnij, że punkty 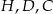 i
i 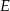 leżą na jednym okręgu.
leżą na jednym okręgu.
Dany jest zbiór wszystkich graniastosłupów prawidłowych sześciokątnych, których suma długości wszystkich krawędzi jest równa 216. Oblicz długość krawędzi podstawy i wysokość tego z danych graniastosłupów, który ma największe pole powierzchni bocznej.
Prosta 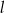 przecina okrąg o środku
przecina okrąg o środku 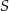 w punktach
w punktach 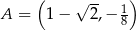 i
i 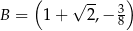 . Punkt
. Punkt 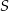 leży na prostej
leży na prostej 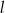 . Oblicz pole koła ograniczonego tym okręgiem.
. Oblicz pole koła ograniczonego tym okręgiem.
Dany jest równoległobok 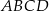 , w którym
, w którym 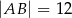 ,
, 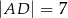 oraz
oraz
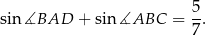
Oblicz pole równoległoboku 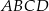 .
.
Przekształcenie 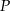 określone jest w następujący sposób:
określone jest w następujący sposób: 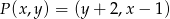 , gdzie
, gdzie 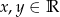 .
.
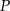 jest izometrią.
jest izometrią. 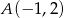 ,
, 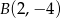 ,
, 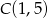 , a następnie znajdź jego obraz w przekształceniu
, a następnie znajdź jego obraz w przekształceniu 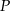 .
. 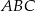 poprowadzoną na bok
poprowadzoną na bok 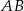 .
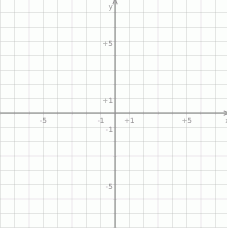
. 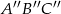 , który jest obrazem trójkąta
, który jest obrazem trójkąta 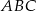 w jednokładności o środku w punkcie (0,0) i skali
w jednokładności o środku w punkcie (0,0) i skali 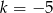 .
.
Dany jest graniastosłup prawidłowy czworokątny, którego suma długości wszystkich krawędzi wynosi 12.
Napisz wzór funkcji 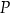 wyrażającej pole powierzchni całkowitej graniastosłupa, w zależności od długości krawędzi podstawy
wyrażającej pole powierzchni całkowitej graniastosłupa, w zależności od długości krawędzi podstawy  . Podaj dziedzinę funkcji
. Podaj dziedzinę funkcji 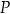 .
.
Wyznacz długości krawędzi graniastosłupa, dla których pole powierzchni całkowitej jest największe.
Wyznacz równanie okręgu o środku 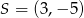 przechodzącego przez początek układu współrzędnych.
przechodzącego przez początek układu współrzędnych.
Wyznacz równanie okręgu o środku 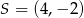 przechodzącego przez punkt
przechodzącego przez punkt 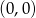 .
.
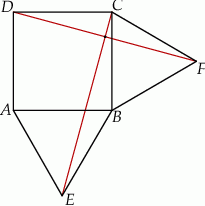
Na zewnątrz kwadratu 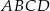 na bokach
na bokach 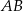 i
i 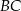 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 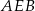 i
i 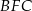 . Uzasadnij, że proste
. Uzasadnij, że proste 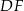 i
i 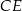 są prostopadłe.
są prostopadłe.
W graniastosłupie prawidłowym sześciokątnym wszystkie krawędzie mają jednakową długość. Oblicz objętość tego graniastosłupa jeżeli jego pole powierzchni całkowitej jest równe 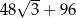 .
.
Wykaż, że punkt przecięcia przekątnych trapezu leży na prostej przechodzącej przez środki jego podstaw.
Przekątna przekroju osiowego walca ma długość 5 cm i jest nachylona do płaszczyzny podstawy pod kątem 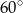 . Jaką długość ma promień podstawy tego walca? Jaka jest jego wysokość?
. Jaką długość ma promień podstawy tego walca? Jaka jest jego wysokość?
Krawędź boczna ostrosłupa prawidłowego czworokątnego jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 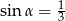 . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
Dany jest trójkąt równoboczny 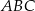 o boku długości 24. Punkt
o boku długości 24. Punkt 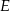 leży na boku
leży na boku 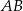 , a punkt
, a punkt 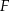 – na boku
– na boku 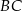 tego trójkąta. Odcinek
tego trójkąta. Odcinek 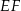 jest równoległy do boku
jest równoległy do boku 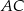 i przechodzi przez środek
i przechodzi przez środek 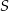 wysokości
wysokości 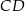 trójkąta
trójkąta 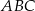 (zobacz rysunek).
(zobacz rysunek).
Oblicz długość odcinka 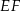 .
.
Wyznacz wszystkie wartości  , dla których liczby
, dla których liczby 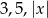 mogą być długościami boków trójkąta.
mogą być długościami boków trójkąta.
