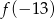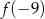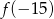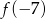Pusta bańka na mleko o pojemności 10 litrów ma masę 6,5 kg. Jeden litr mleka ma masę 1,03 kg. Niech  oznacza liczbę litrów mleka w tej bańce, a
oznacza liczbę litrów mleka w tej bańce, a 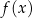 oznacza wyrażoną w kilogramach masę bańki wraz z mlekiem, gdzie
oznacza wyrażoną w kilogramach masę bańki wraz z mlekiem, gdzie ![x ∈ [0,1 0]](https://img.zadania.info/zad/9628036/HzadT2x.png) . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja 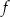 jest malejąca. jest malejąca. | P | F |
Funkcja 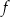 nie ma miejsc zerowych. nie ma miejsc zerowych. | P | F |

 rozwarcia stożka spełnia warunek
rozwarcia stożka spełnia warunek 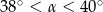
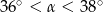
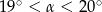
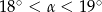
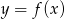 .
. 
 .
. 
 .
. 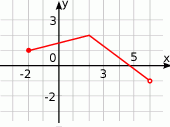
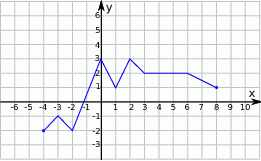
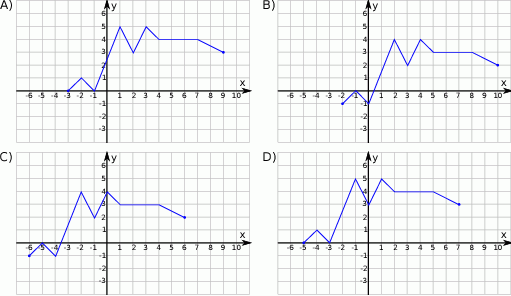
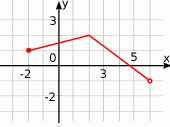
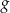 , określonej wzorem
, określonej wzorem 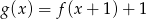 , przedstawia rysunek:
, przedstawia rysunek: 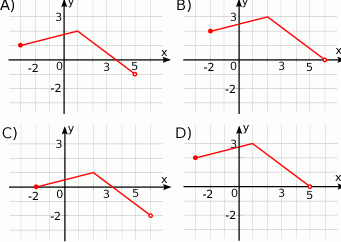
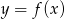 .
. 
 .
. 
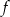 .
. 
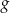 , określonej wzorem
, określonej wzorem 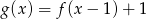 , przedstawia rysunek:
, przedstawia rysunek: 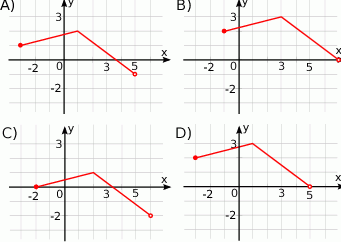
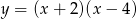 jest równa
jest równa 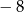
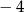
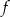 jest określona wzorem
jest określona wzorem 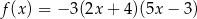 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 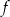 , ma współrzędną
, ma współrzędną  równą
równą 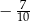
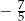
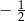
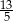
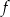 jest określona wzorem
jest określona wzorem 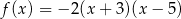 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 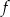 , ma współrzędną
, ma współrzędną  równą
równą 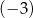
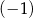
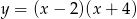 jest równa
jest równa 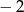
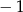
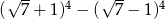 jest równa
jest równa 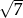
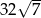
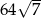
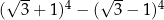 jest równa
jest równa 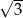
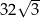
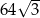
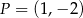 i
i 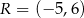 są dwoma sąsiednimi wierzchołkami kwadratu
są dwoma sąsiednimi wierzchołkami kwadratu  . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość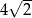
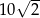
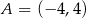 i
i 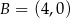 są sąsiednimi wierzchołkami kwadratu
są sąsiednimi wierzchołkami kwadratu 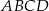 . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość 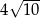
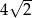
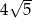
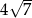
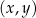 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej  (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji  , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite. 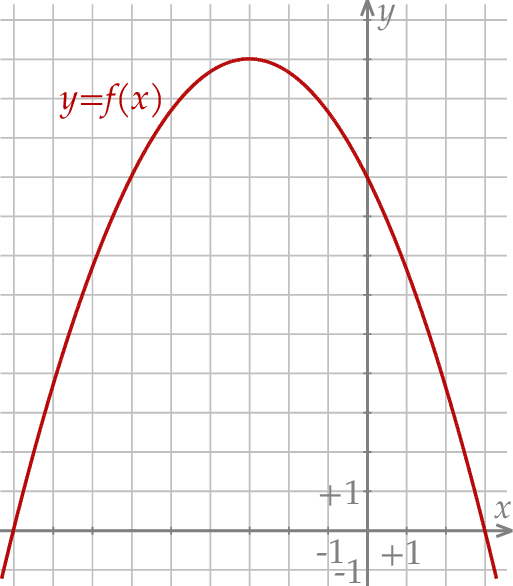
 jest przedział
jest przedział 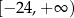
![(− ∞ ,12]](https://img.zadania.info/zad/9642145/HzadT6x.png)
![(− ∞ ,− 12]](https://img.zadania.info/zad/9642145/HzadT7x.png)
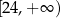
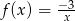 znajduje się w ćwiartkach
znajduje się w ćwiartkach 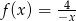 znajduje się w ćwiartkach
znajduje się w ćwiartkach 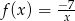 znajduje się w ćwiartkach
znajduje się w ćwiartkach 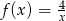 znajduje się w ćwiartkach
znajduje się w ćwiartkach 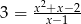 ?
? 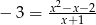 ?
? 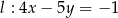 i
i 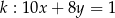
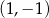
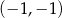
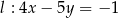 i
i 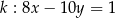
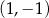
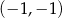
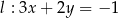 i
i 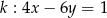
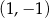
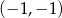
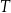 półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa
półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 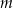 leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą 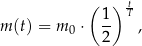
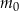 – masa przyjętej dawki leku,
– masa przyjętej dawki leku, 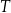 – czas półtrwania leku,
– czas półtrwania leku, 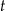 – czas liczony od momentu przyjęcia dawki.
– czas liczony od momentu przyjęcia dawki.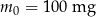 leku L. Czas półtrwania tego leku w organizmie jest równy
leku L. Czas półtrwania tego leku w organizmie jest równy 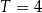 doby.
doby.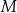 leku L w organizmie tego pacjenta od czasu
leku L w organizmie tego pacjenta od czasu 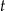 , liczonego od momentu przyjęcia przez pacjenta pierwszej dawki, przedstawiono na rysunku
, liczonego od momentu przyjęcia przez pacjenta pierwszej dawki, przedstawiono na rysunku 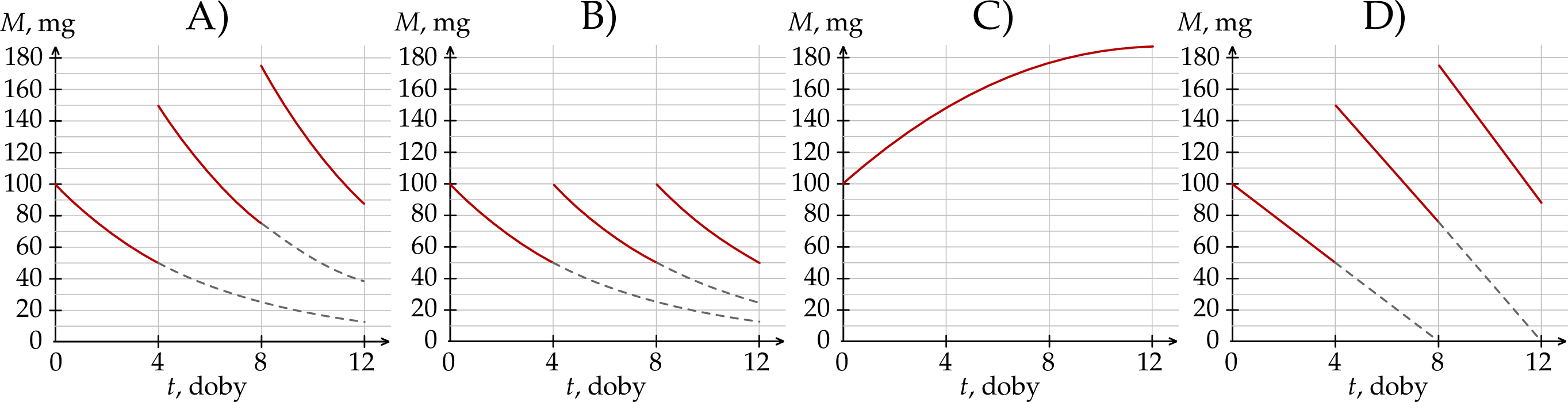
 półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa
półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 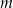 leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą 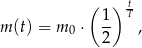
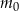 – masa przyjętej dawki leku
– masa przyjętej dawki leku 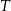 – czas półtrwania leku
– czas półtrwania leku 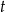 – czas liczony od momentu przyjęcia dawki.
– czas liczony od momentu przyjęcia dawki.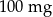 leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę
leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę 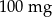 tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy
tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy 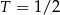 doby.
doby.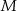 leku L w organizmie pana Karola od czasu
leku L w organizmie pana Karola od czasu  , liczonego od momentu przyjęcia przez niego pierwszej dawki, przedstawiono na rysunku
, liczonego od momentu przyjęcia przez niego pierwszej dawki, przedstawiono na rysunku 
 . Bogdan zapisał te same wyniki w centymetrach i odchylenie standardowe jego danych było równe
. Bogdan zapisał te same wyniki w centymetrach i odchylenie standardowe jego danych było równe 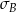 . Wynika stąd, że
. Wynika stąd, że 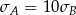
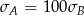
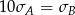
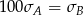
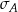 . Basia zapisała te same wyniki w gramach i odchylenie standardowe jej danych było równe
. Basia zapisała te same wyniki w gramach i odchylenie standardowe jej danych było równe 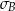 . Wynika stąd, że
. Wynika stąd, że 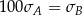
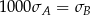
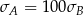
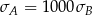
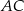 i
i 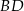 okręgu o środku
okręgu o środku 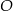 przecinają się w punkcie
przecinają się w punkcie 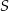 . Ponadto
. Ponadto 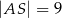 ,
, 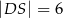 i
i 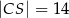 (zobacz rysunek).
(zobacz rysunek). 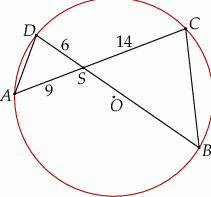
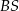 jest równa
jest równa 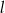 ma równanie
ma równanie 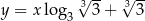 . Wskaż równanie prostej prostopadłej do prostej
. Wskaż równanie prostej prostopadłej do prostej 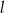 .
.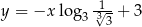
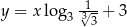
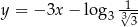
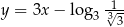
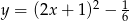 leży na prostej o równaniu
leży na prostej o równaniu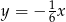
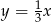
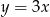
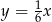
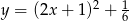 leży na prostej o równaniu
leży na prostej o równaniu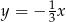
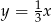
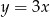
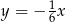
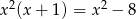 jest
jest 
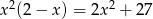 jest
jest 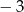
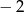
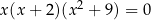 jest
jest 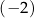
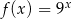 nie należy punkt
nie należy punkt 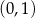
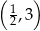
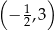
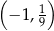
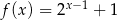 , należy punkt o współrzędnych
, należy punkt o współrzędnych 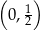
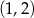
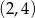
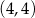
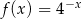 nie należy punkt
nie należy punkt 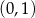
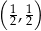
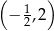
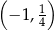
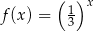 należy punkt
należy punkt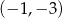
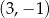
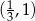
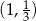
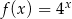 nie należy punkt
nie należy punkt 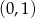
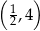
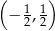
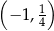
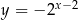 , należy punkt
, należy punkt 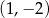
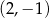
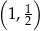
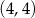
 danej wzorem
danej wzorem 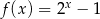 nie należy punkt o współrzędnych
nie należy punkt o współrzędnych 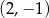
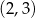
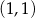
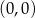
 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  wzorem
wzorem 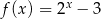 należy punkt o współrzędnych
należy punkt o współrzędnych 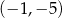
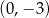
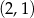
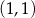
 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  wzorem
wzorem 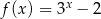 należy punkt o współrzędnych
należy punkt o współrzędnych 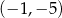
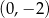
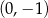
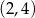
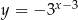 , należy punkt
, należy punkt 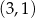
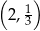
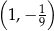
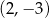
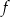 danej wzorem
danej wzorem 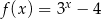 , należy punkt o współrzędnych
, należy punkt o współrzędnych 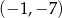
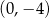
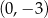
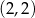
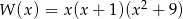 jest równa
jest równa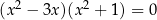 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie 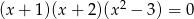 jest równa
jest równa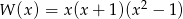 jest równa
jest równa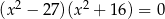 ma dokładnie
ma dokładnie 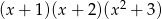 jest równa
jest równa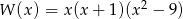 jest równa
jest równa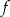 jest określona wzorem
jest określona wzorem 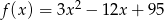 . Zatem wartość
. Zatem wartość 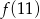 jest równa
jest równa