Funkcja 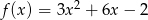 nie przyjmuje wartości
nie przyjmuje wartości
A) 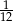 B)
B) 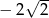 C)
C) 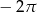 D) 120
D) 120
/Szkoła średnia/Zadania testowe
Funkcja 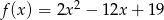 nie przyjmuje wartości
nie przyjmuje wartości
A) 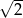 B)
B) 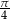 C)
C) 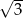 D) 120
D) 120
Funkcja określona wzorem 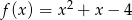 nie przyjmuje wartości
nie przyjmuje wartości
A) -5 B) -4 C) 0 D) 2
Rozwiązaniem układu równań 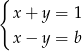 z niewiadomymi
z niewiadomymi  i
i 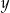 jest para liczb dodatnich. Wynika stąd, że
jest para liczb dodatnich. Wynika stąd, że
A) 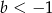 B)
B) 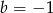 C)
C) 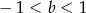 D)
D) 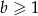
Rozwiązaniem układu równań 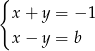 z niewiadomymi
z niewiadomymi  i
i 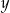 jest para liczb ujemnych. Wynika stąd, że
jest para liczb ujemnych. Wynika stąd, że
A) 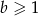 B)
B) 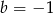 C)
C) 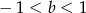 D)
D) 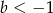
Jeżeli 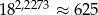 to przybliżona wartość liczby
to przybliżona wartość liczby 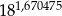 jest równa
jest równa
A) 25 B) 125 C) 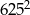 D) 3125
D) 3125
Jeżeli 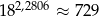 to przybliżona wartość liczby
to przybliżona wartość liczby 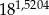 jest równa
jest równa
A) 81 B) 27 C) 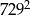 D) 19683
D) 19683
Jeżeli 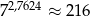 to przybliżona wartość liczby
to przybliżona wartość liczby 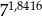 jest równa
jest równa
A) 6 B) 36 C) 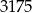 D) 1296
D) 1296
Do zbioru rozwiązań nierówności 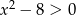 nie należy liczba:
nie należy liczba:
A) -3 B) 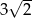 C) 5 D)
C) 5 D) 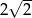
Do zbioru rozwiązań nierówności 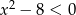 nie należy liczba:
nie należy liczba:
A) -2 B) 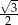 C) -3 D)
C) -3 D) 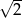
Do zbioru rozwiązań nierówności 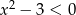 należy liczba:
należy liczba:
A) 2 B) 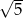 C) -3 D)
C) -3 D) 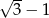
Do zbioru rozwiązań nierówności 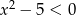 nie należy liczba:
nie należy liczba:
A) 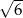 B)
B) 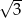 C) 2 D)
C) 2 D) 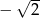
Do zbioru rozwiązań nierówności 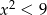 nie należy liczba
nie należy liczba
A) 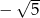 B)
B) 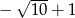 C)
C) 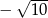 D)
D) 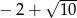
Reszta z dzielenia wielomianu 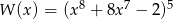 przez dwumian
przez dwumian 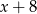 jest równa
jest równa
A) 32 B) 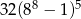 C)
C) 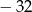 D)
D) 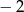
Reszta z dzielenia wielomianu 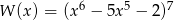 przez dwumian
przez dwumian 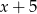 jest równa
jest równa
A) 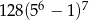 B)
B) 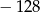 C)
C) 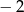 D) 128
D) 128
Reszta z dzielenia wielomianu 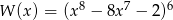 przez dwumian
przez dwumian 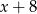 jest równa
jest równa
A) 64 B) 2 C) 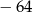 D)
D) 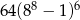
Reszta z dzielenia wielomianu 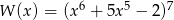 przez dwumian
przez dwumian 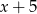 jest równa
jest równa
A) 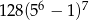 B)
B) 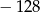 C)
C) 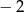 D) 128
D) 128
Reszta z dzielenia wielomianu 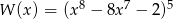 przez dwumian
przez dwumian 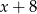 jest równa
jest równa
A) 32 B) 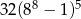 C)
C) 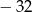 D)
D) 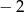
Reszta z dzielenia wielomianu 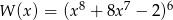 przez dwumian
przez dwumian 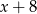 jest równa
jest równa
A) 64 B) 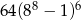 C)
C) 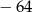 D)
D) 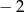
Reszta z dzielenia wielomianu 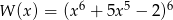 przez dwumian
przez dwumian 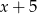 jest równa
jest równa
A) 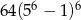 B)
B) 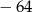 C)
C) 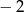 D) 64
D) 64
Dziedziną funkcji 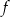 jest przedział
jest przedział 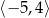 . Obok zamieszczono wykres tej funkcji.
. Obok zamieszczono wykres tej funkcji.
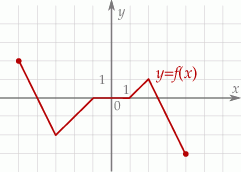
Funkcja 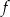 jest malejąca w zbiorze
jest malejąca w zbiorze
A) 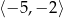 B)
B) 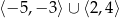 C)
C) 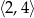 D)
D) 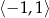
Dziedziną funkcji 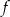 jest przedział
jest przedział 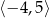 . Poniżej zamieszczono wykres tej funkcji.
. Poniżej zamieszczono wykres tej funkcji.
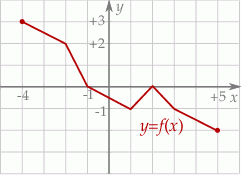
W którym ze zbiorów funkcja 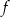 jest malejąca?
jest malejąca?
A) 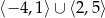 B)
B) 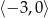 C)
C) 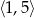 D)
D) 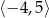
Funkcja, której wykres przedstawiono na rysunku, jest rosnąca w przedziałach
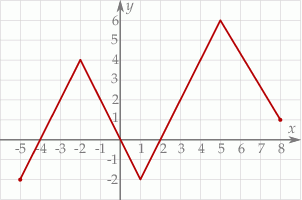
A) 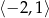 oraz
oraz 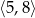 B)
B) 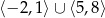 C)
C) 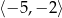 oraz
oraz 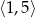 D)
D) 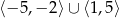
Dziedziną funkcji 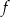 jest przedział
jest przedział 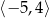 . Obok zamieszczono wykres tej funkcji.
. Obok zamieszczono wykres tej funkcji.
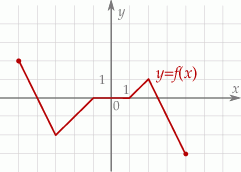
Funkcja 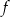 jest rosnąca w zbiorze
jest rosnąca w zbiorze
A) 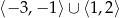 B)
B) 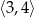 C)
C) 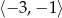 D)
D) 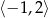
Dziedziną funkcji 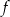 jest przedział
jest przedział 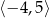 . Poniżej zamieszczono wykres tej funkcji.
. Poniżej zamieszczono wykres tej funkcji.
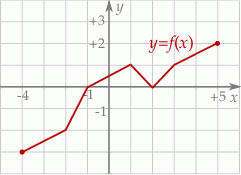
W którym ze zbiorów funkcja 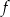 jest rosnąca?
jest rosnąca?
A) 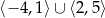 B)
B) 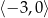 C)
C) 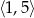 D)
D) 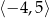
W trójkąt równoboczny wpisano okrąg o równaniu 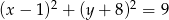 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 9 B) 27 C) 4,5 D) 1
W trójkąt równoboczny wpisano okrąg o równaniu 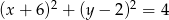 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 12 B) 6 C) 8 D) 4
W trójkąt równoboczny wpisano okrąg o równaniu 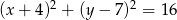 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 48 B) 32 C) 24 D) 12
Funkcja 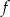 jest określona wzorem
jest określona wzorem 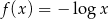 dla wszystkich liczb rzeczywistych dodatnich
dla wszystkich liczb rzeczywistych dodatnich  . Wartość funkcji
. Wartość funkcji 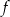 dla argumentu
dla argumentu 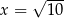 jest równa
jest równa
A) 2 B) 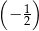 C)
C) 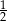 D)
D) 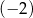
Funkcja 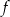 jest określona wzorem
jest określona wzorem 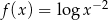 dla wszystkich liczb rzeczywistych dodatnich
dla wszystkich liczb rzeczywistych dodatnich  . Wartość funkcji
. Wartość funkcji 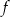 dla argumentu
dla argumentu 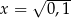 jest równa
jest równa
A) 1 B) 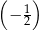 C)
C) 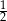 D)
D) 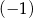
W kartezjańskim układzie współrzędnych 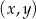 dany jest kwadrat
dany jest kwadrat 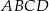 . Wierzchołki
. Wierzchołki 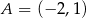 i
i 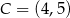 są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu
są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu 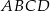 jest równa
jest równa
A) 10 B) 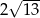 C)
C) 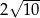 D) 8
D) 8
W kartezjańskim układzie współrzędnych 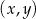 dany jest kwadrat
dany jest kwadrat 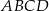 . Wierzchołki
. Wierzchołki 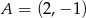 i
i 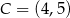 są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu
są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu 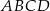 jest równa
jest równa
A) 10 B) 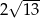 C)
C) 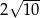 D) 8
D) 8
Mediana dziesięciu liczb naturalnych: 3, 10, 5,  ,
,  ,
,  ,
,  , 12, 19, 7 jest równa 14. Średnia arytmetyczna tych liczb jest równa
, 12, 19, 7 jest równa 14. Średnia arytmetyczna tych liczb jest równa
A) 16 B) 12 C) 12,2 D) 14
Na giełdzie kupiono tę samą liczbę akcji dwóch przedsiębiorstw, przy czym średnia cena zakupu jednej akcji drugiego przedsiębiorstwa była dwa razy wyższa od średniej ceny akcji pierwszego przedsiębiorstwa. Ile średnio zapłacono za jedną akcję drugiego przedsiębiorstwa, jeżeli średnia cena zakupu wszystkich akcji wyniosła 90 zł?
A) 30 zł B) 60 zł C) 90 zł D) 120 zł
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 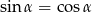 . Przeciwprostokątna tego trójkąta ma długość 2. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 2. Obwód tego trójkąta jest równy
A) 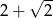 B)
B) 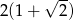 C)
C) 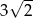 D)
D) 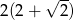
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 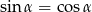 . Przeciwprostokątna tego trójkąta ma długość 6. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 6. Obwód tego trójkąta jest równy
A) 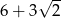 B)
B) 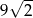 C)
C) 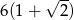 D)
D) 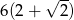
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 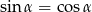 . Przeciwprostokątna tego trójkąta ma długość 5. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 5. Obwód tego trójkąta jest równy
A) 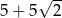 B)
B) 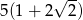 C)
C) 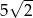 D)
D) 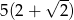
W ciągu geometrycznym 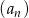 dane są
dane są 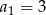 i
i 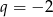 . Suma ośmiu początkowych wyrazów tego ciągu jest równa
. Suma ośmiu początkowych wyrazów tego ciągu jest równa
A) 255 B) -255 C) 257 D) -257
W ciągu geometrycznym 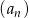 , określonym dla
, określonym dla 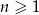 , wyraz
, wyraz 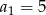 , natomiast iloraz
, natomiast iloraz 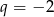 . Suma dziesięciu początkowych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych wyrazów tego ciągu jest równa
A) 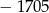 B)
B) 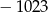 C) 1705 D) 5115
C) 1705 D) 5115
W ciągu geometrycznym 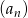 dane są
dane są 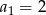 i
i 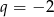 . Suma sześciu początkowych wyrazów tego ciągu jest równa
. Suma sześciu początkowych wyrazów tego ciągu jest równa
A) 86 B) 22 C) 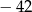 D) 42
D) 42
Odcinki 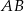 i
i 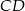 są równoległe. Długości odcinków
są równoległe. Długości odcinków 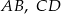 i
i 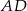 są podane na rysunku.
są podane na rysunku.
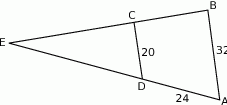
Długość odcinka 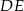 jest równa
jest równa
A) 44 B) 40 C) 36 D) 15
Odcinki 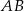 i
i 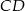 są równoległe i
są równoległe i 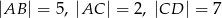 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 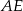 jest równa
jest równa
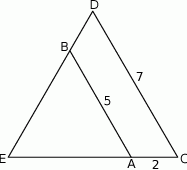
A) 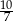 B)
B) 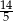 C) 3 D) 5
C) 3 D) 5
Odcinki 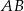 i
i 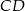 są równoległe. Długości odcinków
są równoległe. Długości odcinków 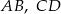 i
i 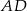 są podane na rysunku.
są podane na rysunku.
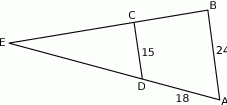
Długość odcinka 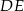 jest równa
jest równa
A) 30 B) 33 C) 27 D) 12
Odcinki 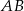 i
i 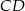 są równoległe i
są równoległe i 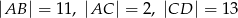 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 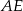 jest równa
jest równa
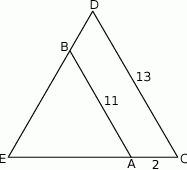
A) 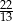 B)
B) 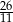 C) 11 D) 13
C) 11 D) 13
Liczba  jest przybliżeniem z niedomiarem liczby
jest przybliżeniem z niedomiarem liczby  . Błąd względny tego przybliżenia jest równy 4%. Liczba
. Błąd względny tego przybliżenia jest równy 4%. Liczba  jest równa
jest równa
A) 0,585 B) 0,65 C) 0,6 D) 0,665
Liczba  jest przybliżeniem z niedomiarem liczby
jest przybliżeniem z niedomiarem liczby  . Błąd względny tego przybliżenia jest równy 2%. Liczba
. Błąd względny tego przybliżenia jest równy 2%. Liczba  jest równa
jest równa
A) 1,225 B) 1,6125 C) 1,2 D) 1,265
Wykres funkcji 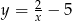 ma jeden punkt wspólny z prostą o równaniu
ma jeden punkt wspólny z prostą o równaniu
A) 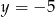 B)
B) 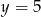 C)
C) 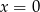 D)
D) 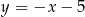
Wykres funkcji 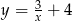 ma jeden punkt wspólny z prostą o równaniu
ma jeden punkt wspólny z prostą o równaniu
A) 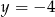 B)
B) 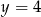 C)
C) 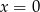 D)
D) 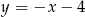
Wykres funkcji 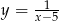 ma jeden punkt wspólny z prostą o równaniu
ma jeden punkt wspólny z prostą o równaniu
A) 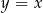 B)
B) 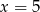 C)
C) 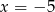 D)
D) 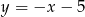
Kąt między ramionami trójkąta równoramiennego ma miarę 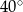 . Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
. Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
A) 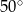 B)
B) 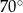 C)
C) 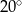 D)
D) 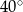
Kąt między ramionami trójkąta równoramiennego wynosi 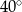 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 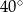 B)
B) 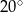 C)
C) 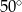 D)
D) 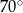
Dany jest trójkąt 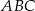 , w którym
, w którym 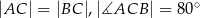 , zaś
, zaś 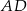 jest wysokością trójkąta. Wówczas miara kąta
jest wysokością trójkąta. Wówczas miara kąta 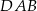 wynosi
wynosi
A) 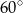 B)
B) 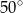 C)
C) 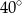 D)
D) 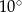
Kąt między ramionami trójkąta równoramiennego ma miarę 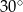 . Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
. Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
A) 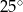 B)
B) 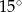 C)
C) 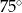 D)
D) 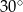
Kąt między ramionami trójkąta równoramiennego wynosi 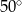 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 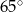 B)
B) 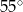 C)
C) 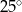 D)
D) 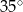
Kąt między ramionami trójkąta równoramiennego ma miarę 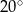 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 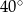 B)
B) 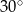 C)
C) 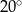 D)
D) 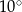
Liczby 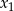 i
i 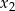 są pierwiastkami równania
są pierwiastkami równania 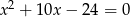 i
i 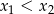 . Oblicz
. Oblicz 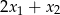 .
.
A) -22 B) -17 C) 8 D) 13
Liczby 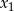 i
i 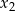 są pierwiastkami równania
są pierwiastkami równania 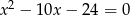 i
i 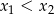 . Oblicz
. Oblicz 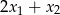 .
.
A) -22 B) -17 C) 8 D) 13
Proste o równaniach 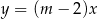 oraz
oraz 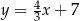 przecinają się w jednym punkcie Wtedy
przecinają się w jednym punkcie Wtedy
A) 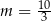 B)
B) 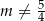 C)
C) 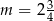 D)
D) 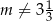
Wiadomo, że mediana liczb 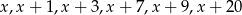 jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 5 B) 26 C) 28 D) 4
Wiadomo, że mediana liczb 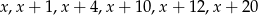 jest równa 11. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 11. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 4 B) 28 C) 22 D) 24
Wiadomo, że mediana liczb 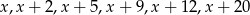 jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 2 B) 16 C) 22 D) 24

