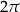W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 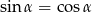 . Przeciwprostokątna tego trójkąta ma długość 2. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 2. Obwód tego trójkąta jest równy
A) 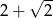 B)
B) 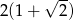 C)
C) 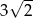 D)
D) 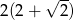
/Szkoła średnia/Zadania testowe
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 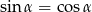 . Przeciwprostokątna tego trójkąta ma długość 5. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 5. Obwód tego trójkąta jest równy
A) 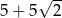 B)
B) 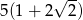 C)
C) 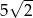 D)
D) 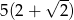
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 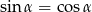 . Przeciwprostokątna tego trójkąta ma długość 6. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 6. Obwód tego trójkąta jest równy
A) 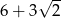 B)
B) 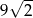 C)
C) 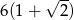 D)
D) 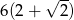
W ciągu geometrycznym 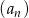 dane są
dane są 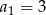 i
i 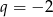 . Suma ośmiu początkowych wyrazów tego ciągu jest równa
. Suma ośmiu początkowych wyrazów tego ciągu jest równa
A) 255 B) -255 C) 257 D) -257
W ciągu geometrycznym 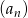 dane są
dane są 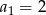 i
i 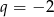 . Suma sześciu początkowych wyrazów tego ciągu jest równa
. Suma sześciu początkowych wyrazów tego ciągu jest równa
A) 86 B) 22 C) 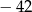 D) 42
D) 42
W ciągu geometrycznym 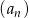 , określonym dla
, określonym dla 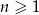 , wyraz
, wyraz 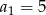 , natomiast iloraz
, natomiast iloraz 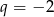 . Suma dziesięciu początkowych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych wyrazów tego ciągu jest równa
A) 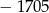 B)
B) 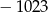 C) 1705 D) 5115
C) 1705 D) 5115
Odcinki 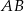 i
i 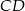 są równoległe. Długości odcinków
są równoległe. Długości odcinków 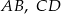 i
i 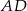 są podane na rysunku.
są podane na rysunku.
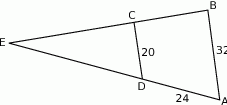
Długość odcinka 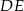 jest równa
jest równa
A) 44 B) 40 C) 36 D) 15
Odcinki 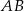 i
i 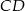 są równoległe i
są równoległe i 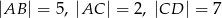 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 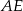 jest równa
jest równa
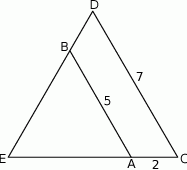
A) 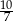 B)
B) 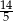 C) 3 D) 5
C) 3 D) 5
Odcinki 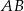 i
i 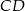 są równoległe. Długości odcinków
są równoległe. Długości odcinków 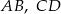 i
i 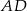 są podane na rysunku.
są podane na rysunku.
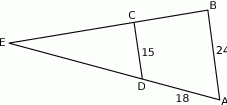
Długość odcinka 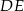 jest równa
jest równa
A) 30 B) 33 C) 27 D) 12
Odcinki 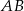 i
i 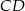 są równoległe i
są równoległe i 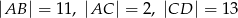 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 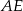 jest równa
jest równa
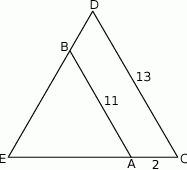
A) 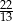 B)
B) 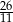 C) 11 D) 13
C) 11 D) 13
Liczba  jest przybliżeniem z niedomiarem liczby
jest przybliżeniem z niedomiarem liczby  . Błąd względny tego przybliżenia jest równy 4%. Liczba
. Błąd względny tego przybliżenia jest równy 4%. Liczba  jest równa
jest równa
A) 0,585 B) 0,65 C) 0,6 D) 0,665
Liczba  jest przybliżeniem z niedomiarem liczby
jest przybliżeniem z niedomiarem liczby  . Błąd względny tego przybliżenia jest równy 2%. Liczba
. Błąd względny tego przybliżenia jest równy 2%. Liczba  jest równa
jest równa
A) 1,225 B) 1,6125 C) 1,2 D) 1,265
Wykres funkcji 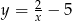 ma jeden punkt wspólny z prostą o równaniu
ma jeden punkt wspólny z prostą o równaniu
A) 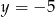 B)
B) 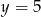 C)
C) 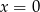 D)
D) 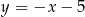
Wykres funkcji 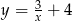 ma jeden punkt wspólny z prostą o równaniu
ma jeden punkt wspólny z prostą o równaniu
A) 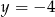 B)
B) 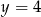 C)
C) 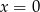 D)
D) 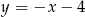
Wykres funkcji 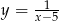 ma jeden punkt wspólny z prostą o równaniu
ma jeden punkt wspólny z prostą o równaniu
A) 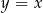 B)
B) 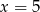 C)
C) 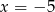 D)
D) 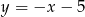
Kąt między ramionami trójkąta równoramiennego ma miarę 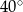 . Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
. Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
A) 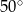 B)
B) 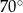 C)
C) 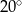 D)
D) 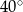
Kąt między ramionami trójkąta równoramiennego wynosi 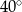 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 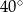 B)
B) 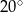 C)
C) 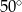 D)
D) 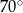
Dany jest trójkąt 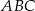 , w którym
, w którym 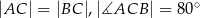 , zaś
, zaś 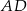 jest wysokością trójkąta. Wówczas miara kąta
jest wysokością trójkąta. Wówczas miara kąta 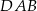 wynosi
wynosi
A) 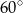 B)
B) 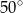 C)
C) 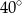 D)
D) 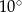
Kąt między ramionami trójkąta równoramiennego ma miarę 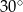 . Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
. Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
A) 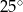 B)
B) 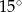 C)
C) 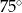 D)
D) 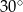
Kąt między ramionami trójkąta równoramiennego wynosi 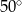 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 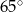 B)
B) 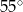 C)
C) 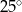 D)
D) 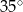
Kąt między ramionami trójkąta równoramiennego ma miarę 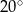 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 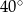 B)
B) 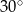 C)
C) 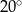 D)
D) 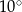
Liczby 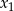 i
i 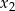 są pierwiastkami równania
są pierwiastkami równania 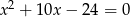 i
i 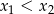 . Oblicz
. Oblicz 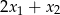 .
.
A) -22 B) -17 C) 8 D) 13
Liczby 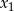 i
i 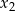 są pierwiastkami równania
są pierwiastkami równania 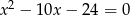 i
i 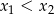 . Oblicz
. Oblicz 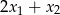 .
.
A) -22 B) -17 C) 8 D) 13
Proste o równaniach 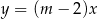 oraz
oraz 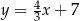 przecinają się w jednym punkcie Wtedy
przecinają się w jednym punkcie Wtedy
A) 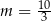 B)
B) 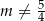 C)
C) 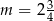 D)
D) 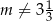
Wiadomo, że mediana liczb 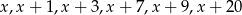 jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 5 B) 26 C) 28 D) 4
Wiadomo, że mediana liczb 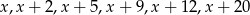 jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 2 B) 16 C) 22 D) 24
Wiadomo, że mediana liczb 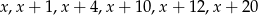 jest równa 11. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 11. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 4 B) 28 C) 22 D) 24
Wyrażenie 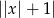 dla
dla 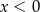 jest równe
jest równe
A) 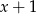 B)
B) 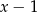 C)
C) 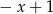 D)
D) 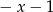
Wyrażenie 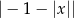 dla
dla 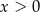 jest równe
jest równe
A) 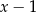 B)
B) 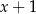 C)
C) 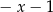 D)
D) 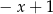
Wyrażenie 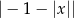 dla
dla 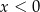 jest równe
jest równe
A) 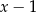 B)
B) 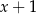 C)
C) 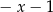 D)
D) 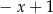
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność 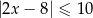 .
.
![]()
Stąd wynika, że
A) 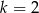 B)
B) 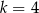 C)
C) 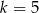 D)
D) 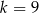
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność 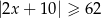 .
.
![]()
Stąd wynika, że
A) 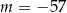 B)
B) 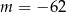 C)
C) 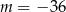 D)
D) 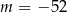
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność 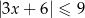 .
.
![]()
Stąd wynika, że
A) 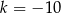 B)
B) 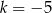 C)
C) 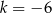 D)
D) 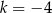
Miejscem zerowym funkcji liniowej 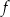 jest liczba 2, a punkt przecięcia wykresu funkcji
jest liczba 2, a punkt przecięcia wykresu funkcji 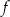 z osią
z osią 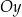 kartezjańskiego układu współrzędnych
kartezjańskiego układu współrzędnych 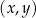 ma współrzędne
ma współrzędne 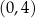 (zobacz rysunek).
(zobacz rysunek).
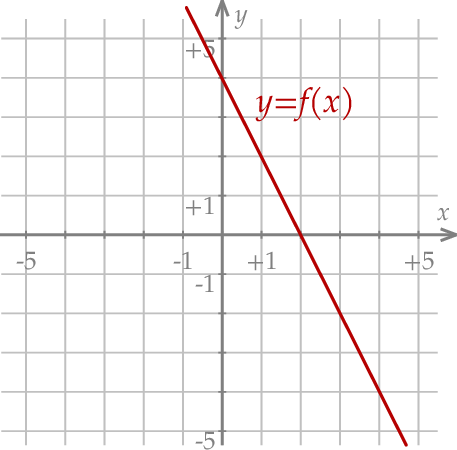
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Współczynnik kierunkowy prostej, która jest wykresem funkcji 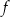 , jest równy , jest równy 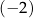 . . | P | F |
Pole trójkąta ograniczonego osiami kartezjańskiego układu współrzędnych 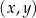 oraz wykresem funkcji oraz wykresem funkcji 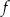 jest równe 8. jest równe 8. | P | F |
Przekątna ściany sześcianu ma długość 8. Przekątna tego sześcianu ma długość
A) 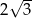 B)
B) 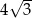 C)
C) 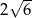 D)
D) 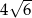
Przekątna ściany sześcianu ma długość 6. Przekątna tego sześcianu ma długość
A) 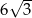 B)
B) 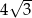 C)
C) 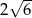 D)
D) 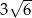
Przekątna ściany sześcianu ma długość 10. Przekątna tego sześcianu ma długość
A) 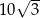 B)
B) 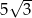 C)
C) 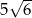 D)
D) 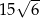
Przekątna ściany sześcianu ma długość 12. Przekątna tego sześcianu ma długość
A) 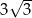 B)
B) 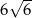 C)
C) 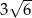 D)
D) 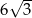
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Dla wszystkich liczb rzeczywistych 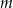 ,
,  i
i 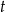 wyrażenie
wyrażenie 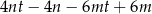 jest równe
jest równe
A) 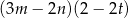 B)
B) 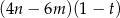
C) 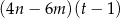 D)
D) 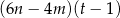
E) 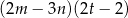 F)
F) 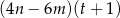
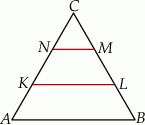
W trójkącie równobocznym 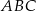 poprowadzono odcinki
poprowadzono odcinki 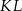 i
i 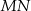 , które podzieliły boki
, które podzieliły boki 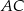 i
i 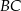 na trzy równe części. Stosunek pola trójkąta
na trzy równe części. Stosunek pola trójkąta 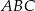 do pola trapezu
do pola trapezu  jest równy
jest równy
A) 3 B) 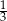 C) 9 D) 6
C) 9 D) 6
Funkcja 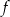 jest określona wzorem
jest określona wzorem 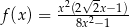 . Wtedy dla argumentu
. Wtedy dla argumentu 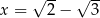 wartość funkcji
wartość funkcji 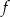 jest równa
jest równa
A) 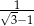 B)
B) 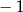 C) 1 D)
C) 1 D) 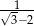
Wartość liczbowa wyrażenia 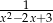 jest największa, gdy liczba
jest największa, gdy liczba  jest równa
jest równa
A) 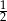 B) 1 C)
B) 1 C) 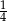 D) 2
D) 2
Wartość liczbowa wyrażenia 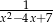 jest największa, gdy liczba
jest największa, gdy liczba  jest równa
jest równa
A) 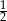 B) 1 C)
B) 1 C) 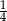 D) 2
D) 2
Wartość liczbowa wyrażenia 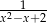 jest największa, gdy liczba
jest największa, gdy liczba  jest równa
jest równa
A) 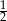 B) 1 C)
B) 1 C) 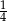 D) 2
D) 2
Jeżeli  jest liczbą ujemną i
jest liczbą ujemną i 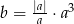 , to
, to
A) 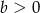 B)
B) 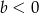 C)
C) 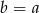 D)
D) 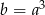
Jeżeli  jest liczbą dodatnią i
jest liczbą dodatnią i 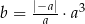 , to
, to
A) 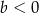 B)
B) 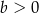 C)
C) 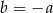 D)
D) 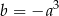
Wskaż wektor równoległy do wektora ![→ v = [− 72 ,9 6]](https://img.zadania.info/zad/4179753/HzadT0x.gif)
A) ![[48,36]](https://img.zadania.info/zad/4179753/HzadT1x.gif) B)
B) ![[45,− 60 ]](https://img.zadania.info/zad/4179753/HzadT2x.gif) C)
C) ![[− 42,64]](https://img.zadania.info/zad/4179753/HzadT3x.gif) D)
D) ![[76,− 57 ]](https://img.zadania.info/zad/4179753/HzadT4x.gif)
Kąt wpisany w okrąg o promieniu 10 ma miarę 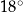 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 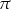 B)
B) 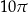 C)
C) 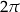 D)
D) 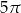
Kąt wpisany w okrąg o promieniu 9 ma miarę 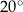 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 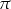 B)
B) 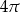 C)
C) 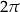 D)
D) 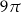
Kąt wpisany w okrąg o promieniu 9 ma miarę 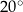 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 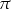 B)
B) 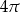 C)
C) 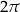 D)
D) 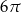
Kąt wpisany w okrąg o promieniu 8 ma miarę 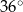 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 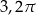 B)
B) 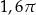 C)
C) 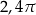 D)
D)