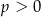Wierzchołek paraboli o równaniu 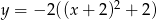 ma współrzędne
ma współrzędne
A) 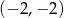 B)
B) 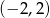 C)
C) 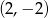 D)
D) 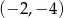
/Szkoła średnia/Zadania testowe/Funkcje - wykresy
Wierzchołek paraboli o równaniu 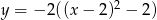 ma współrzędne
ma współrzędne
A) 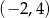 B)
B) 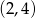 C)
C) 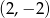 D)
D) 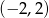
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 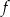 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 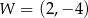 . Liczby 0 i 4 to miejsca zerowe funkcji
. Liczby 0 i 4 to miejsca zerowe funkcji 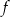 .
.
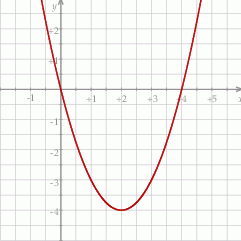
Osią symetrii wykresu funkcji 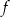 jest prosta o równaniu
jest prosta o równaniu
A) 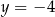 B)
B) 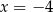 C)
C) 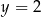 D)
D) 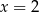
Funkcja kwadratowa 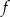 jest określona wzorem
jest określona wzorem 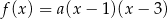 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 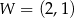 .
.
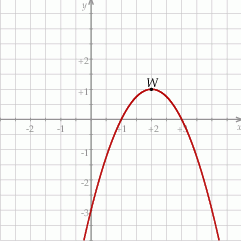
Osią symetrii paraboli będącej wykresem funkcji 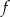 jest prosta o równaniu
jest prosta o równaniu
A) 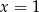 B)
B) 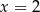 C)
C) 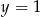 D)
D) 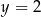
W kartezjańskim układzie współrzędnych 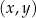 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 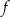 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią 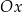 układu współrzędnych mają obie współrzędne całkowite.
układu współrzędnych mają obie współrzędne całkowite.
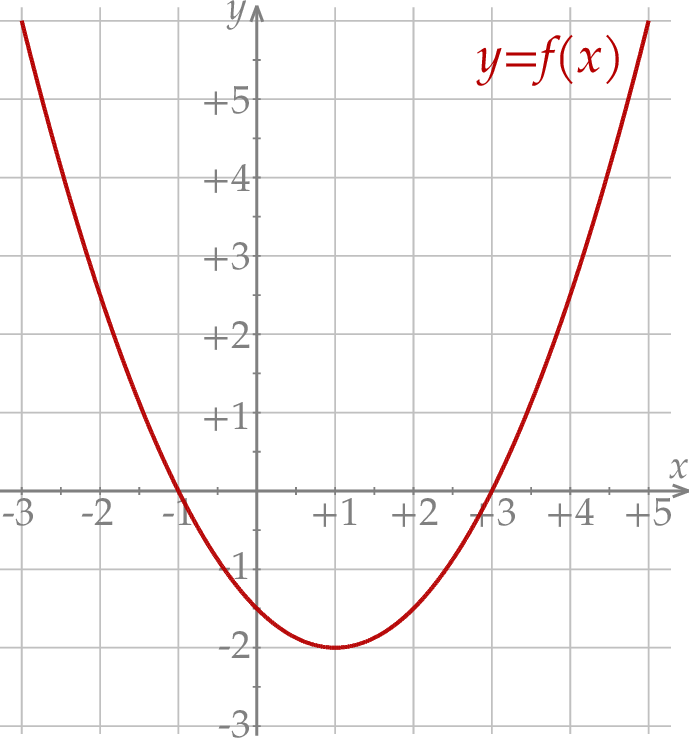
Osią symetrii wykresu funkcji 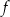 jest prosta o równaniu
jest prosta o równaniu
A) 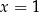 B)
B) 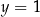 C)
C) 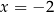 D)
D) 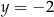
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 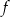 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 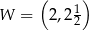 . Liczby
. Liczby 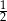 i
i 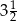 to miejsca zerowe funkcji
to miejsca zerowe funkcji 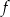 .
.
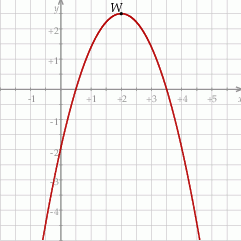
Osią symetrii wykresu funkcji 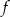 jest prosta o równaniu
jest prosta o równaniu
A) 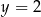 B)
B) 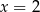 C)
C) 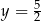 D)
D) 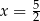
Funkcja kwadratowa 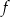 jest określona wzorem
jest określona wzorem 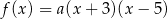 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 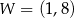 .
.
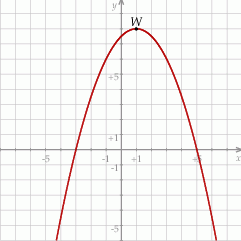
Osią symetrii paraboli będącej wykresem funkcji 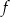 jest prosta o równaniu
jest prosta o równaniu
A) 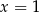 B)
B) 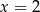 C)
C) 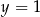 D)
D) 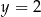
Funkcja liniowa 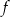 jest określona wzorem
jest określona wzorem 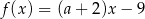 , gdzie
, gdzie  to pewna liczba rzeczywista. Wykres funkcji
to pewna liczba rzeczywista. Wykres funkcji 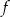 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 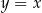 . Stąd wynika, że
. Stąd wynika, że
A) 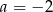 B)
B) 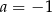 C)
C) 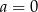 D)
D) 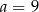
Na rysunku 1 jest przedstawiony wykres funkcji 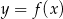 .
.
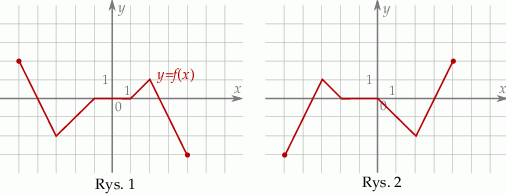
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 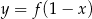 B)
B) 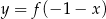 C)
C) 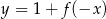 D)
D) 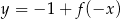
Na rysunku 1 jest przedstawiony wykres funkcji 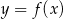 .
.
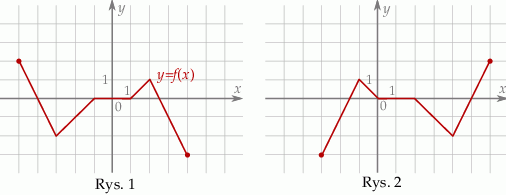
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 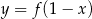 B)
B) 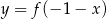 C)
C) 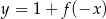 D)
D) 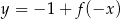
Rysunek przedstawia wykresy funkcji 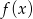 i
i 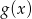 .
.
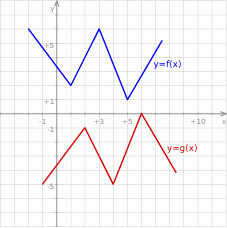
Prawdziwa jest równość:
A) 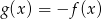 B)
B) 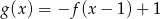 C)
C) 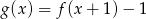 D)
D) 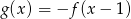
Do wykresu funkcji 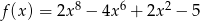 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 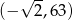 B)
B) 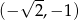 C)
C) 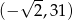 D)
D) 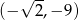
Na rysunku przedstawiono fragmenty dwóch wykresów: funkcji liniowej 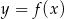 i funkcji
i funkcji ![y = g(x) = [f (x)]2](https://img.zadania.info/zad/3591919/HzadT1x.gif) . Oba wykresy przechodzą przez punkty o współrzędnych
. Oba wykresy przechodzą przez punkty o współrzędnych 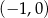 i
i 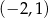 .
.
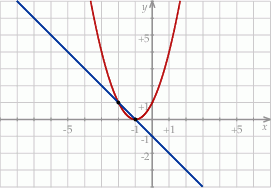
Zbiorem wartości funkcji 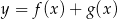 jest przedział
jest przedział
A) 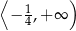 B)
B) 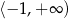 C)
C) 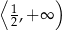 D)
D) 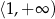
Suma współrzędnych wierzchołka paraboli 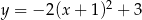 jest równa
jest równa
A) 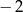 B) 2 C)
B) 2 C) 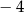 D) 4
D) 4
Do wykresu funkcji 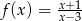 należy punkt
należy punkt
A) 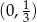 B)
B) 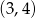 C)
C) 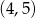 D)
D) 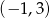
Do wykresu funkcji 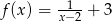 , należy punkt o współrzędnych:
, należy punkt o współrzędnych:
A) 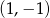 B)
B) 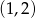 C)
C) 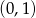 D)
D) 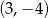
Do wykresu funkcji 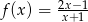 należy punkt
należy punkt
A) 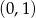 B)
B) 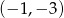 C)
C) 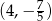 D)
D) 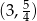
Wykres funkcji 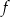 przedstawionej na rysunku powstał przez przesunięcie wykresu funkcji
przedstawionej na rysunku powstał przez przesunięcie wykresu funkcji 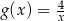 wzdłuż osi odciętych.
wzdłuż osi odciętych.
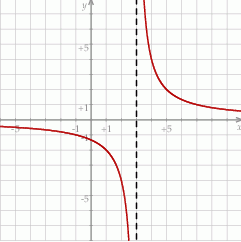
Funkcja 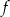 jest określona wzorem
jest określona wzorem
A) 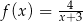 B)
B) 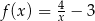 C)
C) 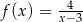 D)
D) 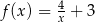
Wskaż wykres funkcji, która w przedziale 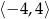 ma dokładnie jedno miejsce zerowe.
ma dokładnie jedno miejsce zerowe.
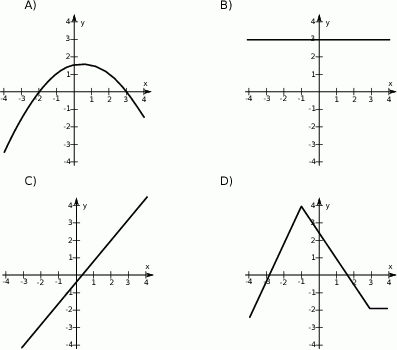
Wskaż wykres funkcji, która w przedziale 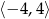 ma dokładnie dwa miejsca zerowe.
ma dokładnie dwa miejsca zerowe.
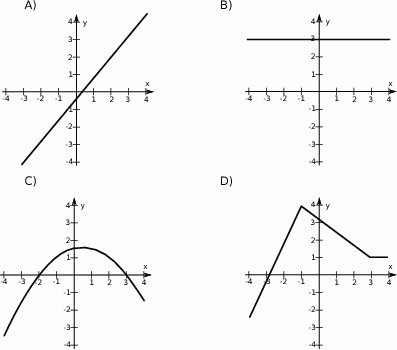
Wskaż wykres funkcji, która w przedziale 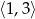 ma dokładnie jedno miejsce zerowe.
ma dokładnie jedno miejsce zerowe.
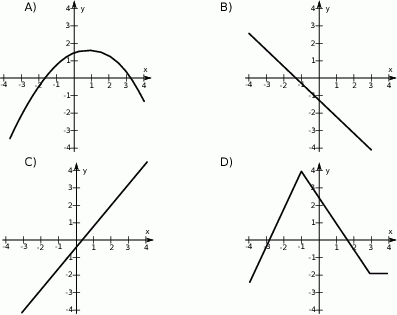
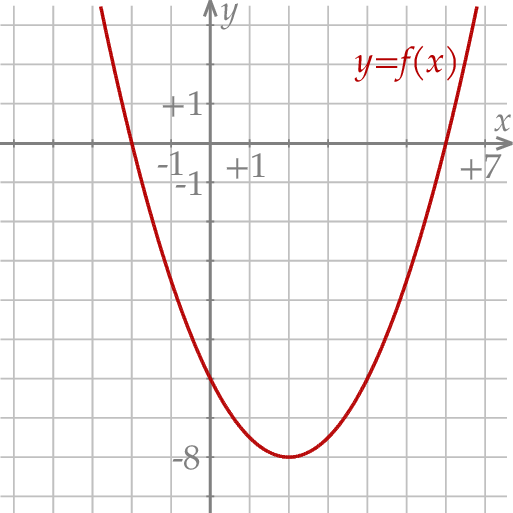
W kartezjańskim układzie współrzędnych 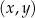 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 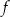 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 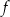 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
Funkcja kwadratowa 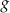 jest określona za pomocą funkcji
jest określona za pomocą funkcji 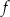 następująco:
następująco: 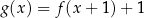 . Fragment wykresu funkcji
. Fragment wykresu funkcji 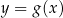 przedstawiono na rysunku
przedstawiono na rysunku
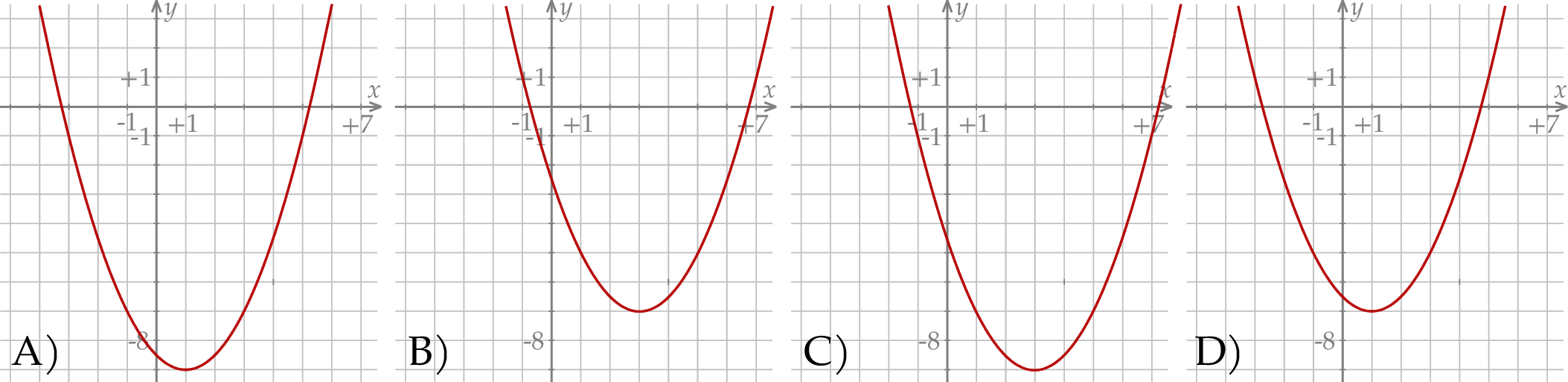
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej 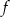 określonej wzorem
określonej wzorem 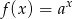 . Punkt
. Punkt 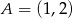 należy do tego wykresu funkcji.
należy do tego wykresu funkcji.
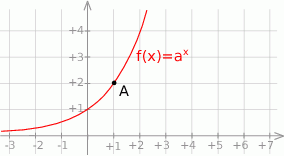
Podstawa  potęgi jest równa
potęgi jest równa
A) 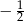 B)
B) 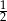 C)
C) 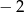 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej 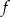 określonej wzorem
określonej wzorem 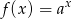 . Punkt
. Punkt 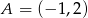 należy do tego wykresu funkcji.
należy do tego wykresu funkcji.
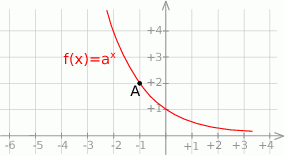
Podstawa  potęgi jest równa
potęgi jest równa
A) 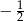 B)
B) 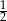 C)
C) 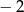 D) 2
D) 2
Wskaż wzór funkcji, której wykres można otrzymać przez przesunięcie wykresu funkcji 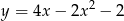 .
.
A) 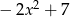 B)
B) 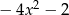 C)
C) 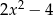 D)
D) 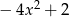
Funkcja kwadratowa o miejscach zerowych 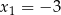 i
i 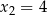 , której wykres przechodzi przez punkt
, której wykres przechodzi przez punkt 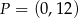 ma wzór:
ma wzór:
A) 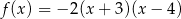 B)
B) 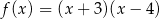
C) 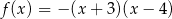 D)
D) 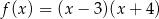
Funkcja kwadratowa o miejscach zerowych 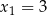 i
i 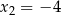 , której wykres przechodzi przez punkt
, której wykres przechodzi przez punkt 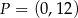 ma wzór:
ma wzór:
A) 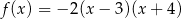 B)
B) 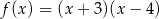
C) 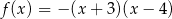 D)
D) 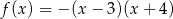
Do wykresu funkcji liniowej określonej wzorem 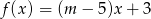 należy punkt
należy punkt 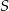 o obu współrzędnych nieparzystych. Liczba
o obu współrzędnych nieparzystych. Liczba 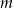 może być równa
może być równa
A) 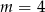 B)
B) 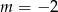 C)
C) 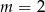 D)
D) 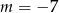
Wykres funkcji 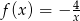 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 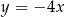 B)
B) 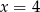 C)
C) 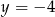 D)
D) 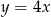
Wykres funkcji 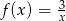 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 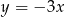 B)
B) 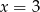 C)
C) 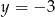 D)
D) 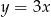
Wykres której z poniższych funkcji nie posiada asymptoty poziomej?
A) 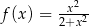 B)
B) 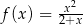 C)
C) 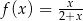 D)
D) 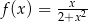
Punkt 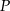 jest punktem przecięcia się wykresów funkcji
jest punktem przecięcia się wykresów funkcji 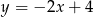 i
i 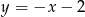 . Punkt
. Punkt 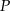 leży w układzie współrzędnych w ćwiartce
leży w układzie współrzędnych w ćwiartce
A) pierwszej B) drugiej C) trzeciej D) czwartej
Punkt 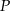 jest punktem przecięcia się wykresów funkcji
jest punktem przecięcia się wykresów funkcji 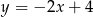 i
i 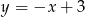 . Punkt
. Punkt 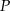 leży w układzie współrzędnych w ćwiartce
leży w układzie współrzędnych w ćwiartce
A) pierwszej B) drugiej C) trzeciej D) czwartej
Punkt 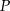 jest punktem przecięcia się wykresów funkcji
jest punktem przecięcia się wykresów funkcji 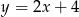 i
i 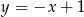 . Punkt
. Punkt 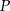 leży w układzie współrzędnych w ćwiartce
leży w układzie współrzędnych w ćwiartce
A) pierwszej B) drugiej C) trzeciej D) czwartej
Na rysunku przedstawiony jest wykres funkcji 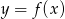 .
.
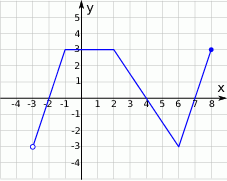
Największą wartością funkcji
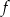 jest
jest A) 3 B) 0 C)
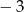 D) 8
D) 8 Na rysunku przedstawiony jest wykres funkcji 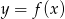 .
.
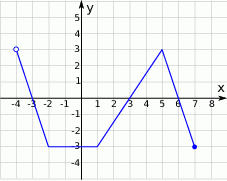
Najmniejszą wartością funkcji 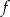 jest
jest
A) 3 B) 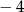 C)
C) 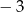 D) 7
D) 7
Na rysunku, w układzie współrzędnych 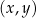 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 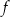 .
.
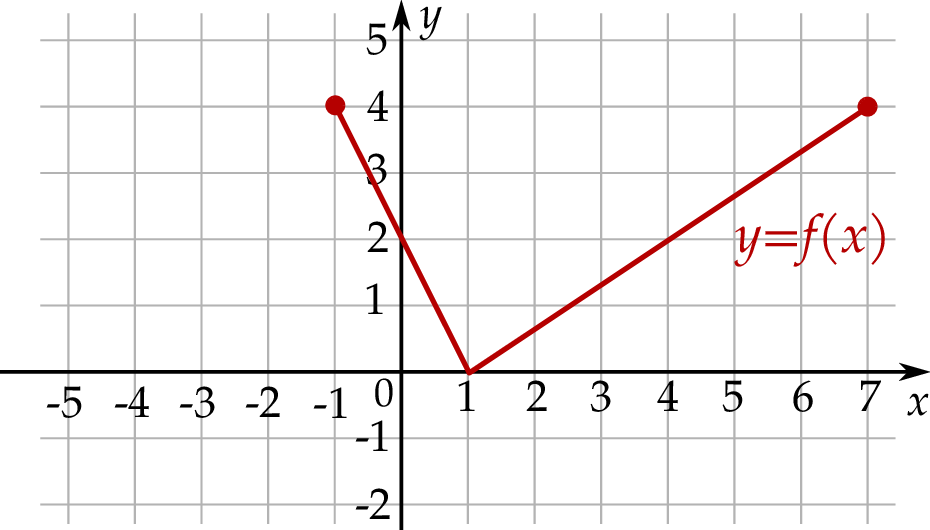
Największa wartość funkcji
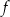 jest równa
jest równa A) 2 B) 4 C) 6 D) 7
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 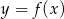 , której dziedziną jest zbiór
, której dziedziną jest zbiór 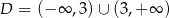 .
.
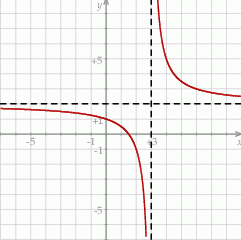
Równanie 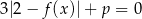 z niewiadomą
z niewiadomą  ma dokładnie dwa rozwiązania tylko wtedy, gdy
ma dokładnie dwa rozwiązania tylko wtedy, gdy
A) 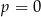 B)
B) 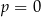 lub
lub 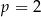 C)
C) 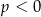 D)
D)