Funkcja 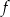 określona jest wzorem
określona jest wzorem 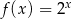 . Funkcja
. Funkcja 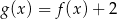 z prostą
z prostą 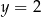
A) ma jeden punkt wspólny B) dwa punkty wspólne
C) nie ma punktów wspólnych D) ma nieskończenie wiele punktów wspólnych
/Szkoła średnia/Zadania testowe/Funkcje - wykresy
Funkcja 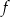 określona jest wzorem
określona jest wzorem 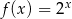 . Wykres funkcji
. Wykres funkcji 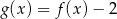 z prostą
z prostą 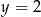
A) ma jeden punkt wspólny B) dwa punkty wspólne
C) nie ma punktów wspólnych D) ma nieskończenie wiele punktów wspólnych
Wykres funkcji kwadratowej 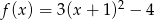 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 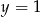 B)
B) 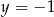 C)
C) 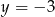 D)
D) 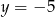
Wykres funkcji kwadratowej 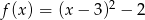 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 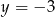 B)
B) 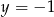 C)
C) 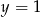 D)
D) 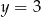
Wykres funkcji kwadratowej 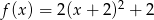 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 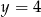 B)
B) 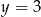 C)
C) 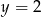 D)
D) 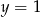
Punkt 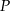 jest punktem wspólnym wykresów funkcji
jest punktem wspólnym wykresów funkcji 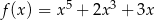 i
i 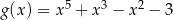 . Zatem suma współrzędnych punktu
. Zatem suma współrzędnych punktu 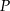
A) jest liczbą większą od 3 B) jest liczbą z przedziału 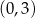
C) jest liczbą naturalną D) jest liczbą mniejszą od -3
Dziedziną funkcji 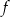 jest przedział
jest przedział 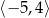 . Obok zamieszczono wykres tej funkcji.
. Obok zamieszczono wykres tej funkcji.
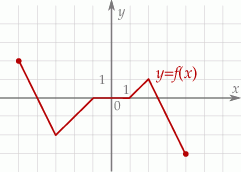
Funkcja 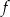 jest malejąca w zbiorze
jest malejąca w zbiorze
A) 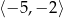 B)
B) 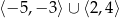 C)
C) 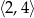 D)
D) 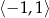
Dziedziną funkcji 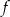 jest przedział
jest przedział 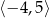 . Poniżej zamieszczono wykres tej funkcji.
. Poniżej zamieszczono wykres tej funkcji.
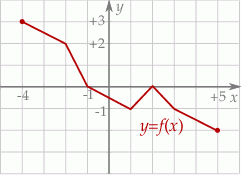
W którym ze zbiorów funkcja 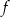 jest malejąca?
jest malejąca?
A) 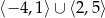 B)
B) 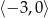 C)
C) 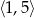 D)
D) 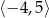
Funkcja, której wykres przedstawiono na rysunku, jest rosnąca w przedziałach
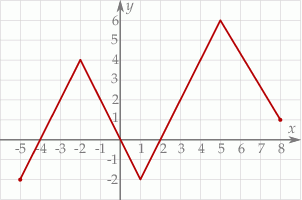
A) 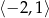 oraz
oraz 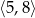 B)
B) 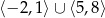 C)
C) 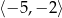 oraz
oraz  D)
D) 
Dziedziną funkcji 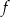 jest przedział
jest przedział 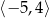 . Obok zamieszczono wykres tej funkcji.
. Obok zamieszczono wykres tej funkcji.
Funkcja 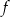 jest rosnąca w zbiorze
jest rosnąca w zbiorze
A) 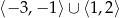 B)
B) 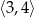 C)
C) 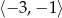 D)
D) 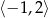
Dziedziną funkcji 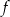 jest przedział
jest przedział 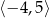 . Poniżej zamieszczono wykres tej funkcji.
. Poniżej zamieszczono wykres tej funkcji.
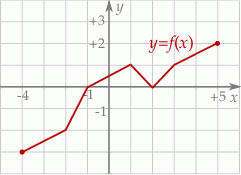
W którym ze zbiorów funkcja 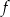 jest rosnąca?
jest rosnąca?
A) 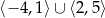 B)
B) 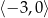 C)
C) 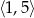 D)
D) 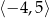
Wykres funkcji 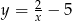 ma jeden punkt wspólny z prostą o równaniu
ma jeden punkt wspólny z prostą o równaniu
A) 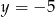 B)
B) 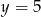 C)
C) 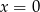 D)
D) 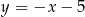
Wykres funkcji 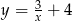 ma jeden punkt wspólny z prostą o równaniu
ma jeden punkt wspólny z prostą o równaniu
A) 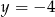 B)
B) 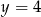 C)
C) 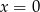 D)
D) 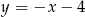
Wykres funkcji 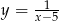 ma jeden punkt wspólny z prostą o równaniu
ma jeden punkt wspólny z prostą o równaniu
A) 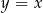 B)
B) 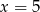 C)
C) 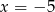 D)
D) 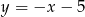
Jeżeli do wykresu funkcji wykładniczej 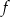 należy punkt
należy punkt 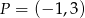 , to funkcja ta określona jest wzorem
, to funkcja ta określona jest wzorem
A) 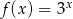 B)
B) 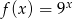 C)
C) 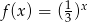 D)
D) 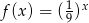
Jeżeli do wykresu funkcji wykładniczej 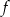 należy punkt
należy punkt 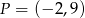 , to funkcja ta określona jest wzorem
, to funkcja ta określona jest wzorem
A) 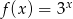 B)
B) 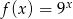 C)
C) 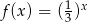 D)
D) 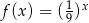
Jeżeli do wykresu funkcji wykładniczej 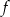 należy punkt
należy punkt 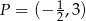 , to funkcja ta określona jest wzorem
, to funkcja ta określona jest wzorem
A) 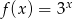 B)
B) 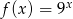 C)
C) 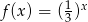 D)
D) 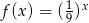
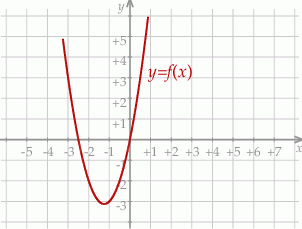
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 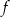 określonej wzorem
określonej wzorem 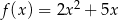 .
.
Funkcja kwadratowa
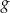 jest określona wzorem
jest określona wzorem 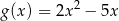 . Wykres funkcji
. Wykres funkcji 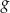 jest
jest A) symetryczny do wykresu funkcji
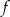 względem osi
względem osi 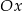 .
. B) symetryczny do wykresu funkcji
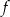 względem osi
względem osi 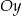 .
. C) symetryczny do wykresu funkcji
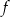 względem początku układu współrzędnych.
względem początku układu współrzędnych. D) przesunięty względem wykresu funkcji
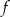 o 10 jednostek w kierunku przeciwnym do zwrotu osi
o 10 jednostek w kierunku przeciwnym do zwrotu osi 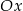 .
. Dane są funkcje liniowe 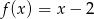 oraz
oraz 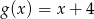 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 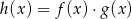 .
.
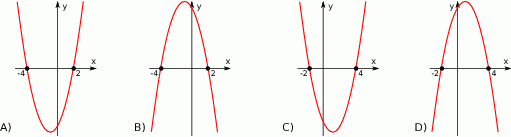
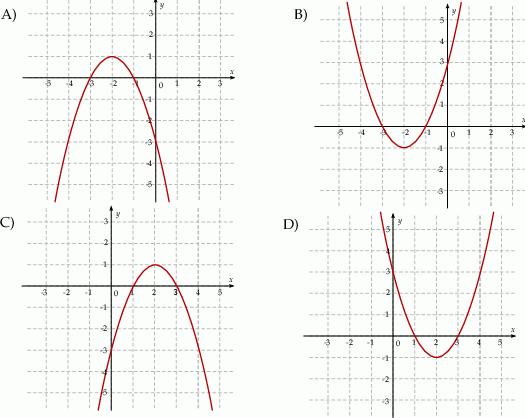
Dane są funkcje liniowe 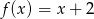 oraz
oraz 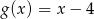 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 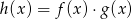 .
.
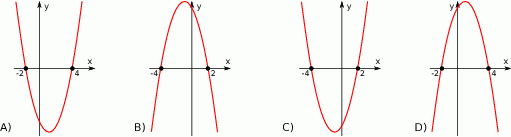
Funkcja kwadratowa 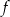 jest określona wzorem
jest określona wzorem 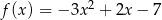 . Wykresem funkcji
. Wykresem funkcji 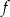 jest parabola, której wierzchołek leży na prostej o równaniu
jest parabola, której wierzchołek leży na prostej o równaniu
A) 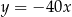 B)
B) 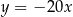 C)
C) 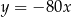 D)
D) 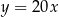
Na rysunkach poniżej znajdują się wykresy dwóch funkcji: 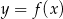 oraz
oraz 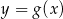 .
.
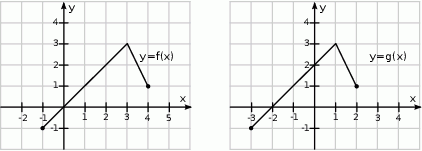
Zatem:
A) 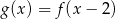 B)
B) 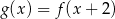
C) 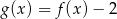 D)
D) 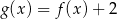
Na rysunku, w układzie współrzędnych 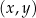 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 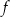 .
.
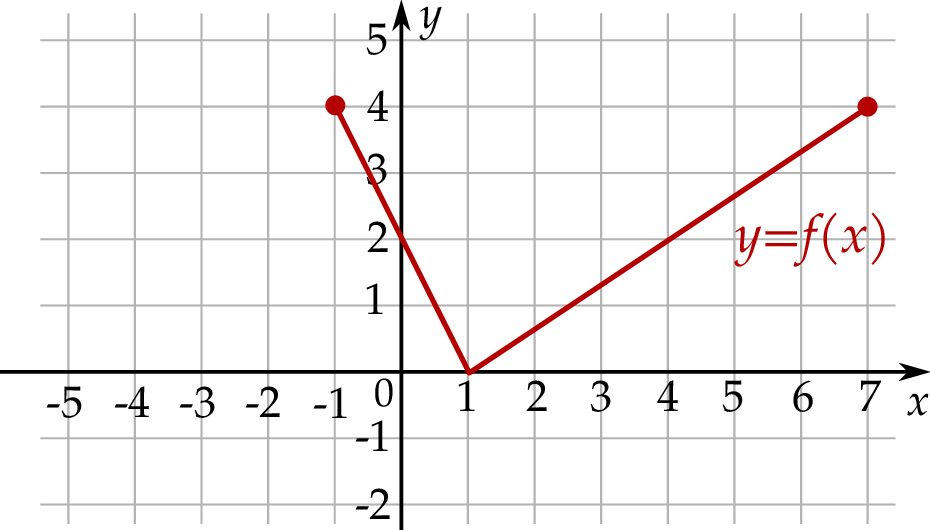
Na drugim rysunku przedstawiono wykres funkcji
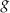 , powstałej w wyniku przesunięcia równoległego wykresu funkcji
, powstałej w wyniku przesunięcia równoległego wykresu funkcji 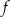 wzdłuż osi
wzdłuż osi 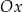 o 4 jednostki w lewo.
o 4 jednostki w lewo. 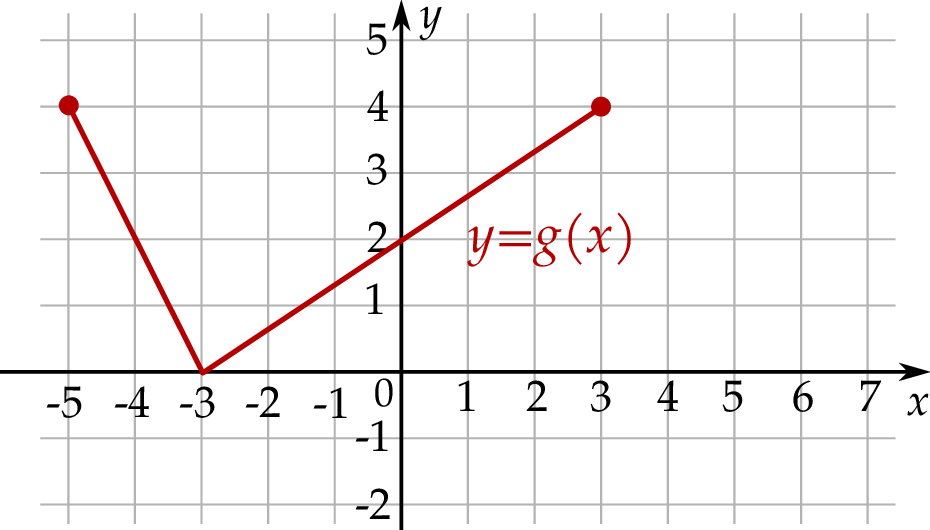
Funkcje 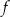 i
i 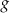 są powiązane zależnością
są powiązane zależnością
A) 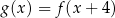 B)
B) 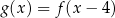
C) 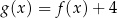 D)
D) 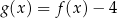
Na rysunku 1 przedstawiony jest wykres funkcji 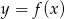 określonej dla
określonej dla 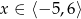 .
.
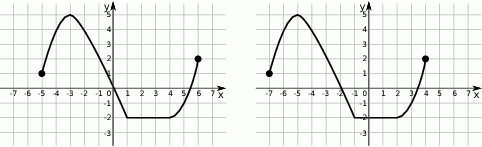
Rysunek 2 przedstawia wykres funkcji
A) 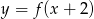 B)
B) 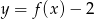 C)
C) 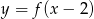 D)
D) 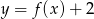
Na rysunku 1. przedstawiono wykres funkcji 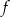 określonej na zbiorze
określonej na zbiorze 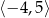 . Funkcję
. Funkcję 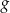 określono za pomocą funkcji
określono za pomocą funkcji 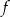 . Wykres funkcji
. Wykres funkcji 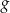 przedstawiono na rysunku 2.
przedstawiono na rysunku 2.
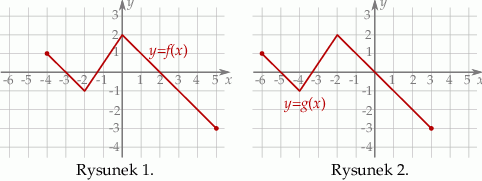
Wynika stąd, że
A) 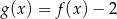 B)
B) 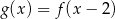
C) 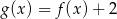 D)
D) 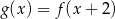
Na rysunku 1 przedstawiony jest wykres funkcji 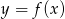 określonej dla
określonej dla 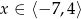 .
.
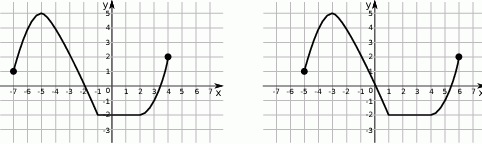
Rysunek 2 przedstawia wykres funkcji
A) 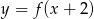 B)
B) 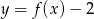 C)
C) 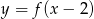 D)
D) 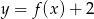
Funkcja liniowa 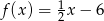
A) jest malejąca i jej wykres przechodzi przez punkt 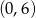
B) jest rosnąca i jej wykres przechodzi przez punkt 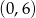
C) jest malejąca i jej wykres przechodzi przez punkt 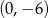
D) jest rosnąca i jej wykres przechodzi przez punkt 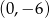
Funkcja liniowa 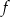 określona jest wzorem
określona jest wzorem 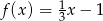 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych  . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Funkcja 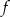 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś 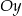 w punkcie
w punkcie 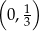
B) Funkcja  jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś  w punkcie
w punkcie 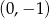
C) Funkcja  jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś  w punkcie
w punkcie 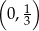
D) Funkcja 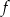 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 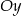 w punkcie
w punkcie 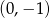
Funkcja liniowa 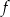 określona jest wzorem
określona jest wzorem 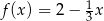 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych  . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Funkcja 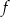 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś  w punkcie
w punkcie 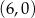
B) Funkcja 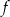 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś 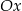 w punkcie
w punkcie 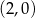
C) Funkcja 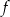 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 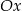 w punkcie
w punkcie 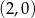
D) Funkcja 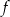 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 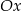 w punkcie
w punkcie 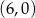
Wskaż funkcję, której wykres przecina prostą o równaniu 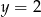 w punkcie o dodatnich współrzędnych.
w punkcie o dodatnich współrzędnych.
A) 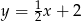 B)
B) 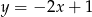 C)
C) 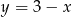 D)
D) 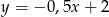
Wskaż funkcję, której wykres przecina prostą o równaniu 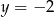 w punkcie o ujemnych współrzędnych.
w punkcie o ujemnych współrzędnych.
A) 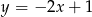 B)
B) 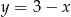 C)
C) 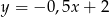 D)
D) 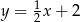
Ile punktów wspólnych z osią 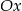 ma wykres funkcji kwadratowej
ma wykres funkcji kwadratowej 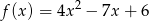 ?
?
A) 0 B) 1 C) 2 D) 3
Wykres funkcji liniowej 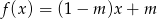 przechodzi przez I, II i III ćwiartkę układu współrzędnych wtedy i tylko wtedy, gdy:
przechodzi przez I, II i III ćwiartkę układu współrzędnych wtedy i tylko wtedy, gdy:
A) 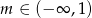 B)
B) 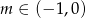 C)
C) 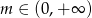 D)
D) 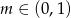
Wykres funkcji liniowej 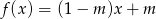 przechodzi przez I, III i IV ćwiartkę układu współrzędnych wtedy i tylko wtedy, gdy
przechodzi przez I, III i IV ćwiartkę układu współrzędnych wtedy i tylko wtedy, gdy
A) 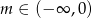 B)
B) 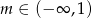 C)
C) 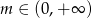 D)
D) 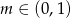
Wykres funkcji określonej na zbiorze liczb rzeczywistych:
A) musi mieć punkt wspólny z osią 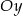 ,
,
B) może mieć dwa punkty wspólne z osią 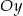 ,
,
C) musi mieć punkt wspólny z osią 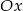 ,
,
D) przechodzi przez początek układu współrzędnych.
Wykres funkcji określonej na zbiorze liczb rzeczywistych:
A) może nie mieć punktów wspólnych z osią 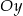 ,
,
B) może mieć dwa punkty wspólne z osią 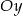 ,
,
C) musi mieć punkt wspólny z osią 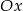 ,
,
D) może mieć dwa punkty wspólnych z osią 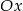 .
.
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej 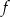 określonej wzorem
określonej wzorem 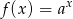 . Wartość funkcji dla
. Wartość funkcji dla 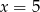 jest cztery razy większa, niż wartość dla
jest cztery razy większa, niż wartość dla 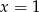 .
.
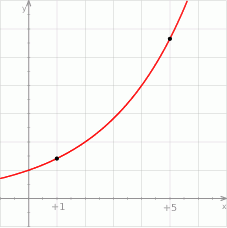
Podstawa  potęgi jest równa
potęgi jest równa
A) 2 B) 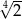 C)
C) 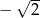 D)
D) 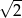
Wykres funkcji 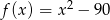 ma dokładnie jeden punkt wspólny z prostą o równaniu
ma dokładnie jeden punkt wspólny z prostą o równaniu
A) 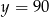 B)
B) 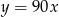 C)
C) 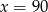 D)
D) 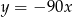
Dana jest funkcja kwadratowa 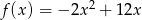 . Wykres tej funkcji ma dokładnie jeden punkt wspólny z prostą o równaniu
. Wykres tej funkcji ma dokładnie jeden punkt wspólny z prostą o równaniu
A) 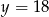 B)
B) 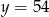 C)
C) 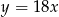 D)
D) 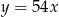
Wykres funkcji 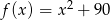 ma dokładnie jeden punkt wspólny z prostą o równaniu
ma dokładnie jeden punkt wspólny z prostą o równaniu
A) 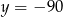 B)
B) 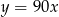 C)
C) 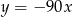 D)
D) 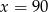
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 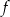 . Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji
. Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji 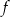 należy punkt
należy punkt 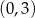 . Prosta o równaniu
. Prosta o równaniu 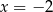 jest osią symetrii paraboli, będącej wykresem funkcji
jest osią symetrii paraboli, będącej wykresem funkcji  .
.
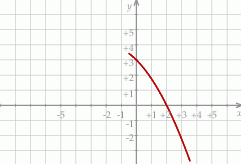
Wartość funkcji 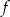 dla argumentu
dla argumentu 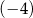 jest równa
jest równa
A) 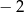 B) 0 C) 3 D) 4
B) 0 C) 3 D) 4
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 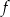 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 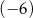 . Do wykresu funkcji
. Do wykresu funkcji 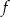 należy punkt
należy punkt 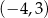 . Prosta o równaniu
. Prosta o równaniu 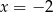 jest osią symetrii paraboli, będącej wykresem funkcji
jest osią symetrii paraboli, będącej wykresem funkcji 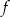 .
.
Wartość funkcji 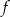 dla argumentu 0 jest równa
dla argumentu 0 jest równa
A) 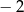 B) 0 C) 3 D) 4
B) 0 C) 3 D) 4
W kartezjańskim układzie współrzędnych 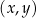 narysowano wykres funkcji
narysowano wykres funkcji 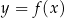 (zobacz rysunek).
(zobacz rysunek).
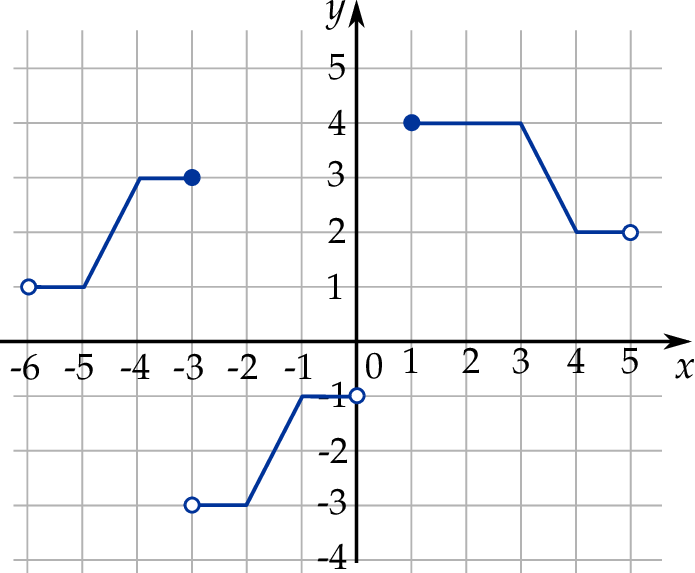
Dziedziną funkcji 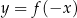 jest zbiór
jest zbiór
A) 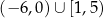 B)
B) 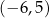 C)
C) ![(− 3,− 1)∪ (1,4]](https://img.zadania.info/zad/4829582/HzadT6x.png)
D) 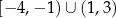 E)
E) ![(− 5,− 1]∪ (0,6)](https://img.zadania.info/zad/4829582/HzadT8x.png) F)
F) 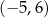
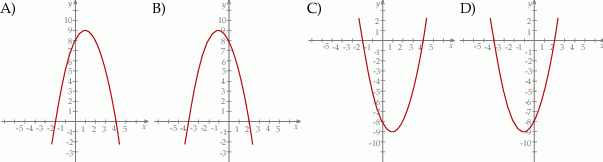
Wskaż rysunek, na którym przedstawiony jest wykres funkcji kwadratowej, określonej wzorem 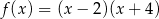 .
.
Na jednym z rysunków przedstawiono fragment wykresu funkcji kwadratowej określonej wzorem 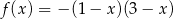 . Wskaż ten rysunek.
. Wskaż ten rysunek.
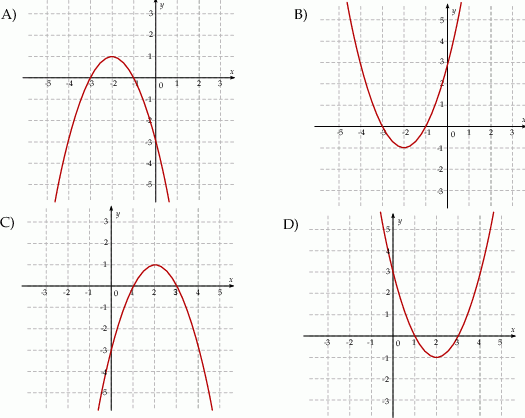
Wskaż rysunek, na którym przedstawiony jest wykres funkcji kwadratowej, określonej wzorem 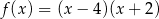 .
.
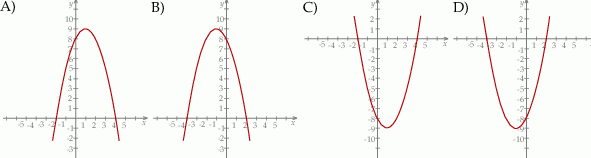
Na jednym z rysunków przedstawiono fragment wykresu funkcji kwadratowej określonej wzorem 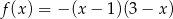 . Wskaż ten rysunek.
. Wskaż ten rysunek.