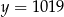W kartezjańskim układzie współrzędnych 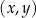 narysowano wykres funkcji
narysowano wykres funkcji 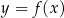 (zobacz rysunek).
(zobacz rysunek).
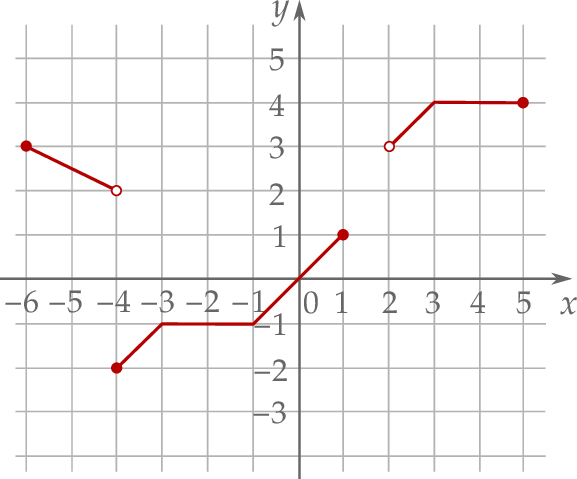
Wskaż przedział, który nie zawiera się w dziedzinie funkcji 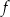 .
.
A) ![[− 6,− 4]](https://img.zadania.info/zad/3001188/HzadT4x.png) B)
B) ![[− 5,− 3]](https://img.zadania.info/zad/3001188/HzadT5x.png) C)
C) ![[− 1,3]](https://img.zadania.info/zad/3001188/HzadT6x.png) D)
D) ![[3,5]](https://img.zadania.info/zad/3001188/HzadT7x.png)
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W kartezjańskim układzie współrzędnych 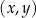 narysowano wykres funkcji
narysowano wykres funkcji 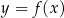 (zobacz rysunek).
(zobacz rysunek).

Wskaż przedział, który nie zawiera się w dziedzinie funkcji 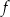 .
.
A) ![[− 6,− 4]](https://img.zadania.info/zad/3001188/HzadT4x.png) B)
B) ![[− 5,− 3]](https://img.zadania.info/zad/3001188/HzadT5x.png) C)
C) ![[− 1,3]](https://img.zadania.info/zad/3001188/HzadT6x.png) D)
D) ![[3,5]](https://img.zadania.info/zad/3001188/HzadT7x.png)
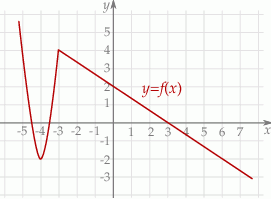
Na rysunku poniżej przedstawiony jest wykres funkcji liniowej 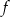 .
.
Funkcja to może być określona wzorem
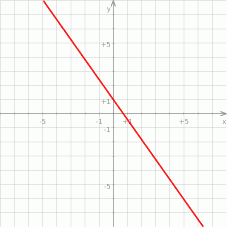
A) 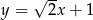 B)
B)  C)
C) 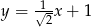 D)
D) 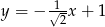
Na rysunku poniżej przedstawiony jest wykres funkcji liniowej 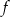 .
.
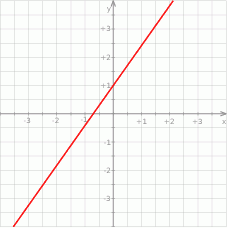
Funkcja ta może być określona wzorem
A) 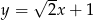 B)
B) 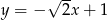 C)
C) 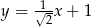 D)
D) 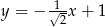
Rysunek przedstawia wykres funkcji 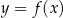 .
.
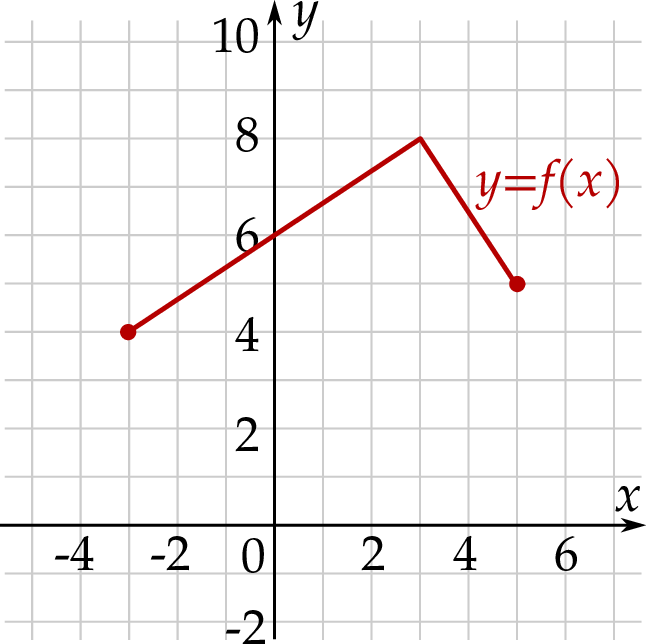
Wskaż rysunek, na którym przedstawiony jest wykres funkcji  .
.
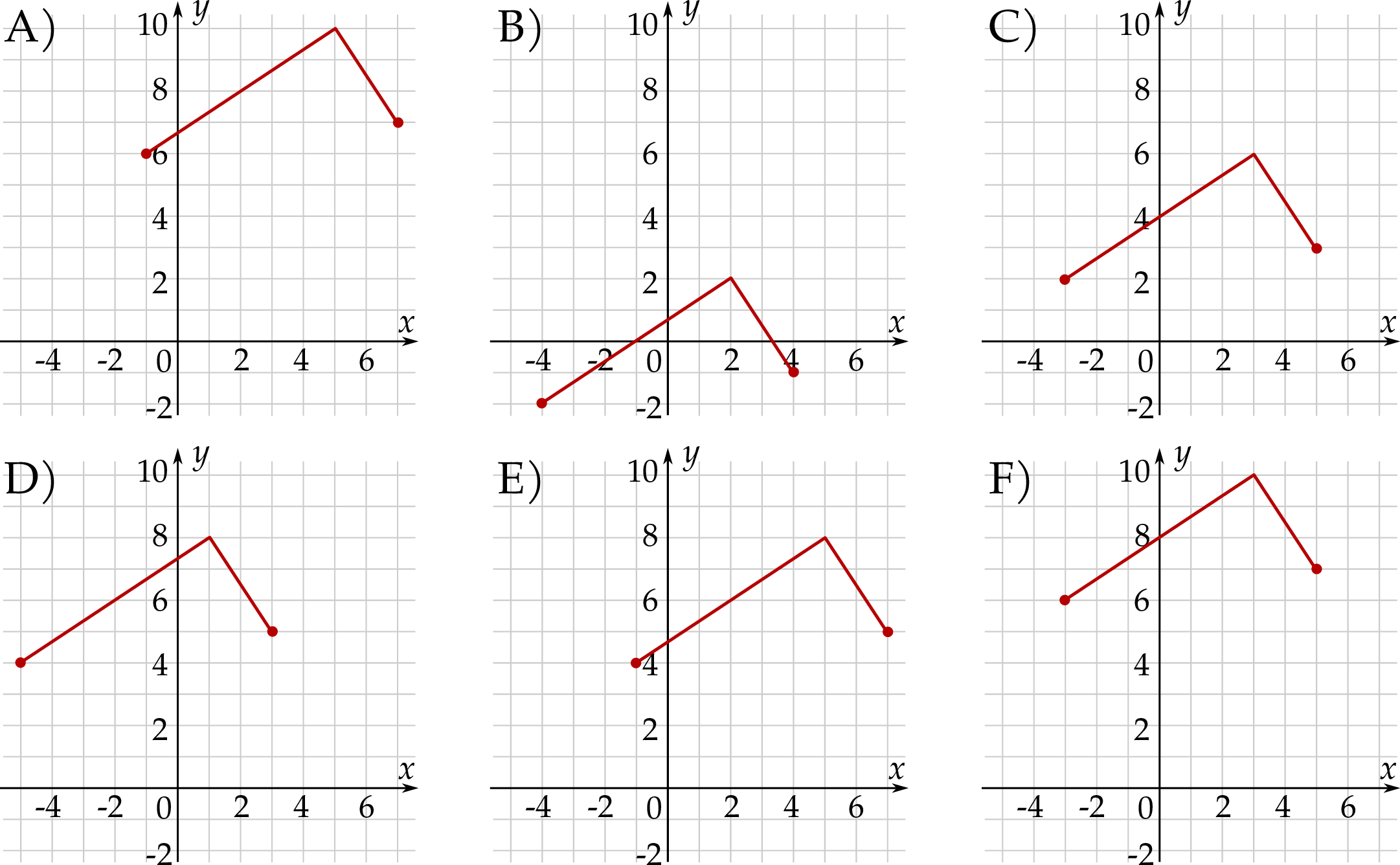
Rysunek przedstawia wykres funkcji 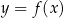 .
.
Wskaż rysunek, na którym przedstawiony jest wykres funkcji  .
.
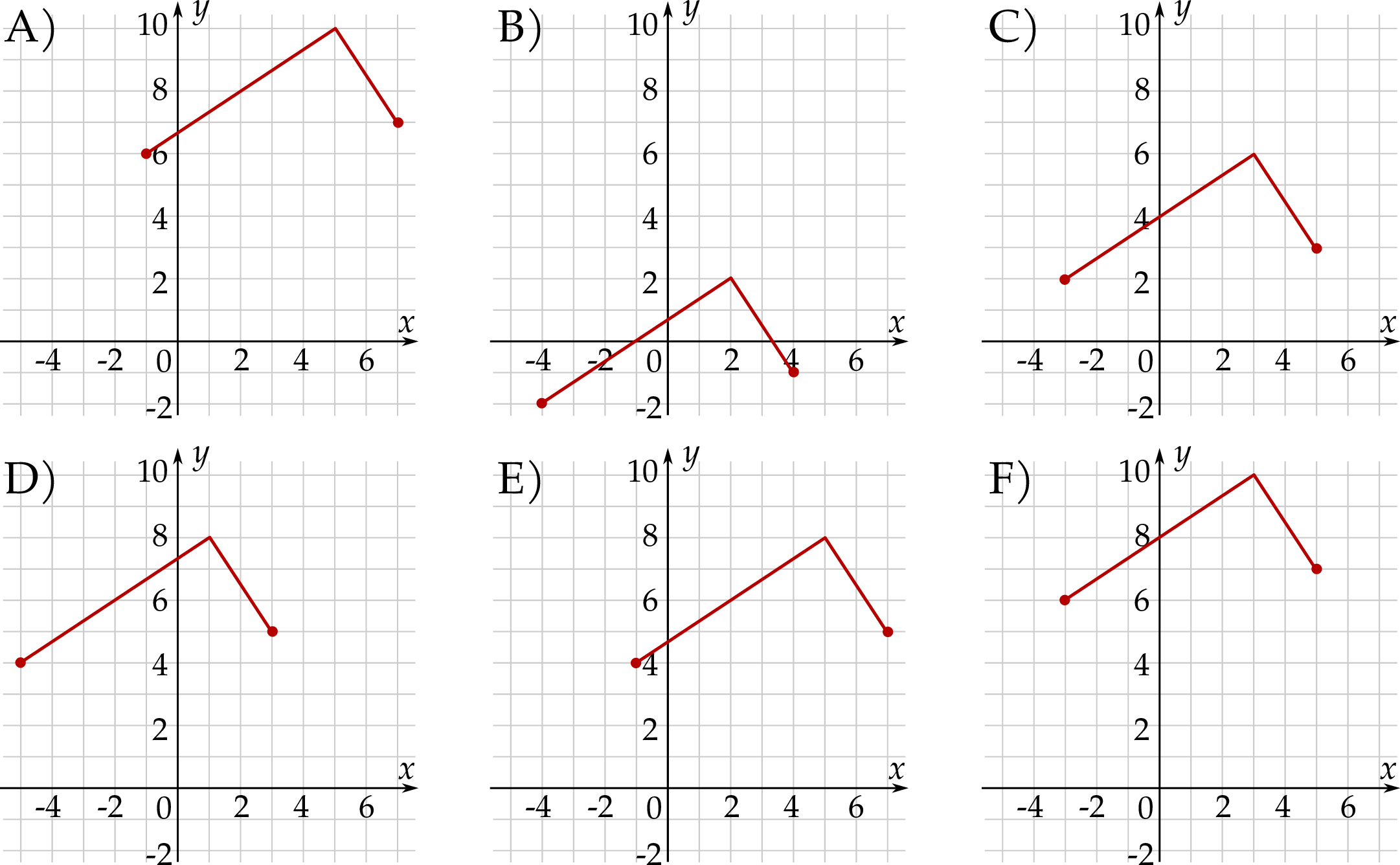
Na rysunku przedstawiono fragment wykresu pochodnej 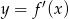 funkcji
funkcji 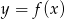 .
.
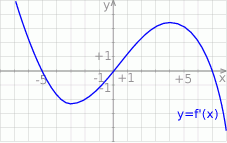
Wynika stąd, że funkcja 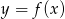 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 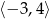 B)
B) 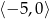 C)
C) 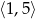 D)
D) 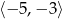
Na rysunku przedstawiono fragment wykresu pochodnej 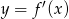 funkcji
funkcji 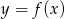 .
.
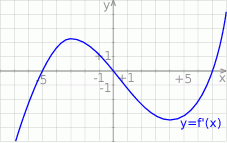
Wynika stąd, że funkcja 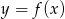 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 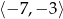 B)
B) 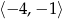 C)
C) 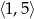 D)
D) 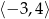
Do wykresu funkcji 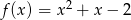 należy punkt
należy punkt
A) 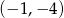 B)
B) 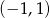 C)
C) 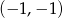 D)
D) 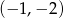
Do wykresu funkcji 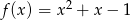 należy punkt
należy punkt
A) 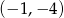 B)
B) 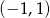 C)
C) 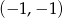 D)
D) 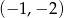
Do wykresu funkcji 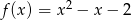 należy punkt
należy punkt
A) 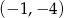 B)
B) 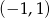 C)
C) 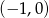 D)
D) 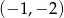
Do wykresu funkcji 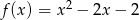 należy punkt
należy punkt
A) 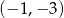 B)
B) 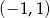 C)
C) 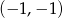 D)
D) 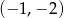
Wykres funkcji 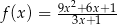 i prosta
i prosta 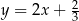
A) pokrywają się B) mają jeden punkt wspólny
C) są rozłączne D) mają dwa punkty wspólne
Wskaż równanie paraboli, której osią symetrii jest prosta 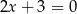 .
.
A) 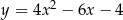 B)
B) 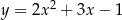
C) 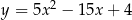 D)
D) 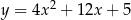
Wskaż równanie paraboli, której osią symetrii jest prosta 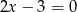 .
.
A) 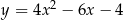 B)
B) 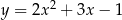
C) 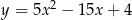 D)
D) 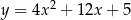
Wykresem funkcji 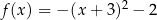 jest:
jest:
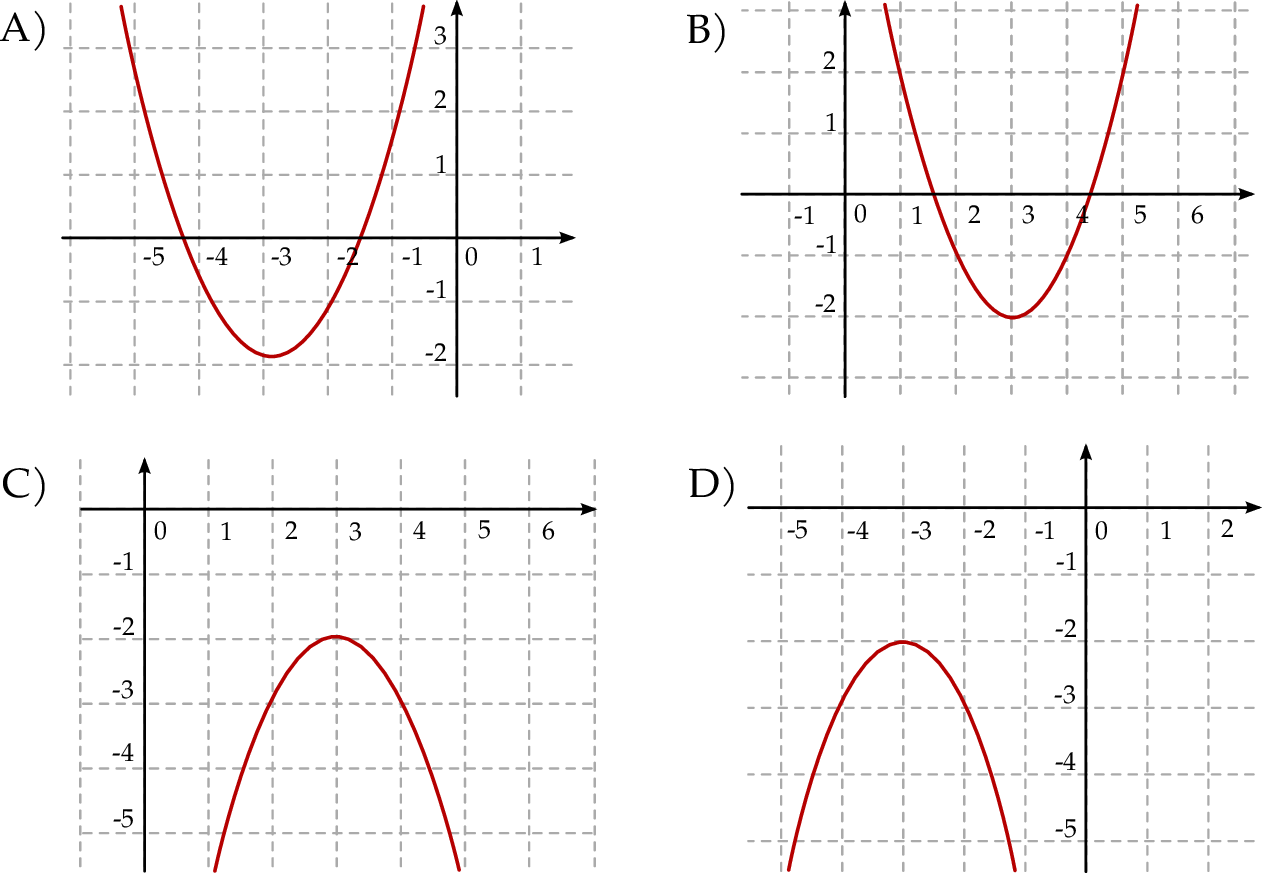
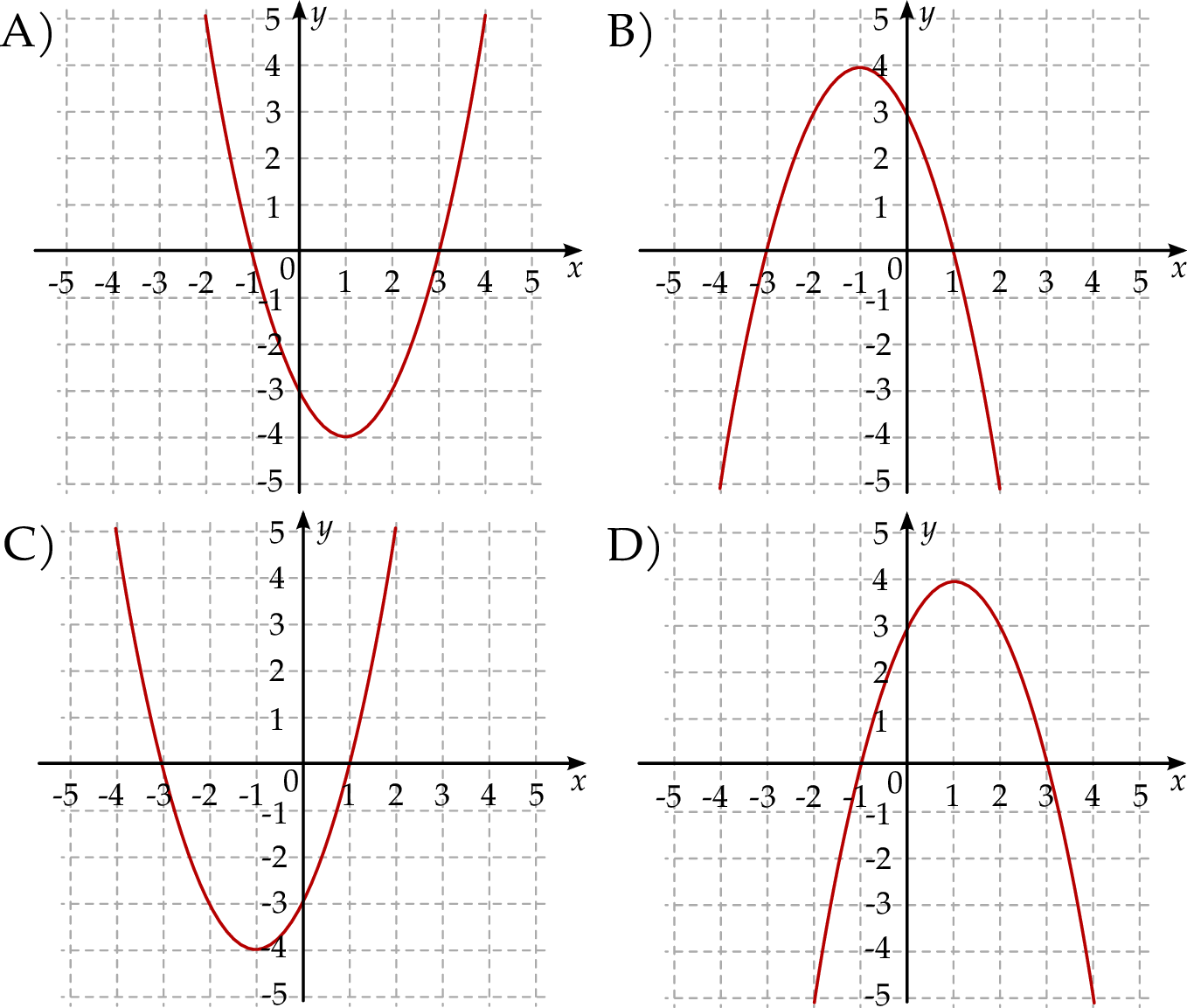
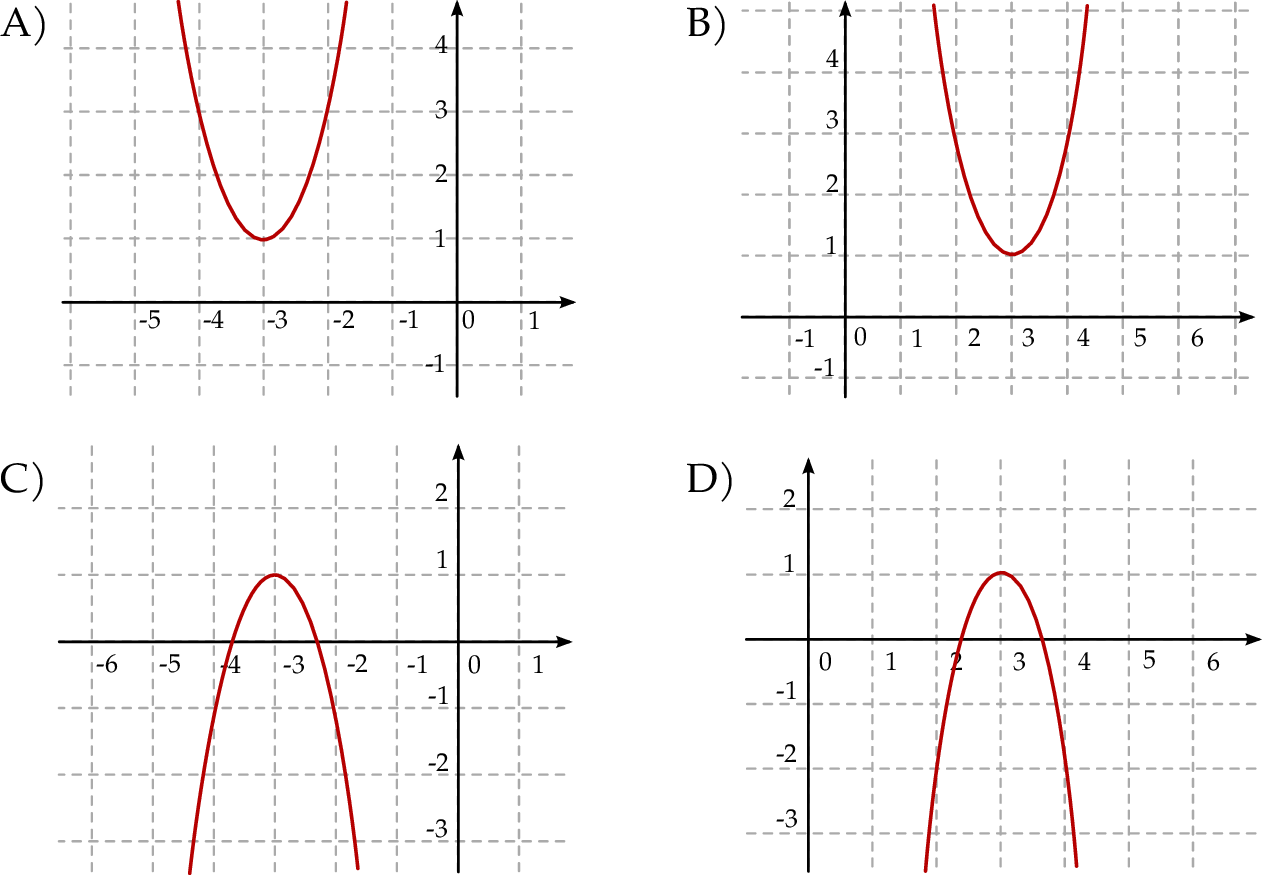
Funkcja kwadratowa 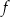 jest określona wzorem
jest określona wzorem 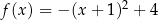 . Fragment wykresu funkcji
. Fragment wykresu funkcji 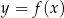 przedstawiono na rysunku
przedstawiono na rysunku
Wykres funkcji 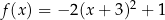 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
Wierzchołek paraboli będącej wykresem funkcji 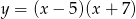 ma współrzędne
ma współrzędne
A) 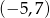 B)
B) 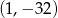 C)
C) 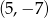 D)
D) 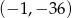
Współrzędne wierzchołka paraboli będącej wykresem funkcji 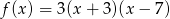 są równe
są równe
A) 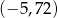 B)
B) 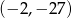 C)
C) 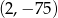 D)
D) 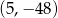
Wierzchołek paraboli będącej wykresem funkcji 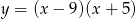 ma współrzędne
ma współrzędne
A) 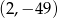 B)
B) 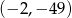 C)
C) 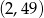 D)
D) 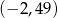
Współrzędne wierzchołka paraboli będącej wykresem funkcji 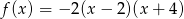 są równe
są równe
A) 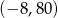 B)
B) 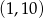 C)
C) 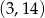 D)
D) 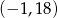
Wierzchołek paraboli będącej wykresem funkcji 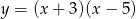 ma współrzędne
ma współrzędne
A) 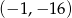 B)
B) 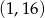 C)
C) 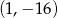 D)
D) 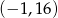
Współrzędne wierzchołka paraboli będącej wykresem funkcji 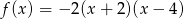 są równe
są równe
A) 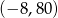 B)
B) 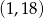 C)
C) 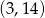 D)
D) 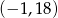
Na rysunku przedstawiono wykres funkcji kwadratowej postaci 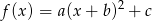 .
.
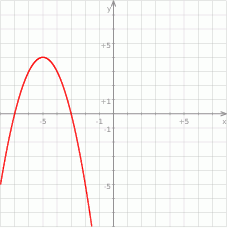
Zatem
A) 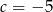 B)
B) 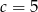 C)
C) 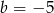 D)
D) 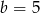
Jeżeli wykres funkcji 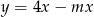 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 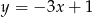 to
to
A) 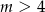 B)
B) 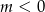 C)
C) 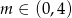 D)
D) 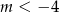
W kartezjańskim układzie współrzędnych 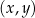 wykresy funkcji liniowych
wykresy funkcji liniowych 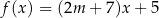 oraz
oraz 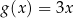 nie mają punktów wspólnych dla
nie mają punktów wspólnych dla
A) 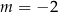 B)
B) 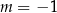 C)
C) 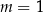 D)
D) 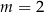
W kartezjańskim układzie współrzędnych 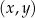 wykresy funkcji liniowych
wykresy funkcji liniowych 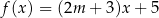 oraz
oraz 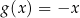 nie mają punktów wspólnych dla
nie mają punktów wspólnych dla
A) 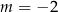 B)
B) 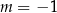 C)
C) 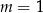 D)
D) 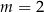
W kartezjańskim układzie współrzędnych 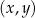 wykresy funkcji liniowych
wykresy funkcji liniowych 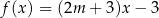 oraz
oraz 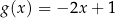 nie mają punktów wspólnych dla
nie mają punktów wspólnych dla
A) 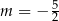 B)
B) 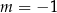 C)
C) 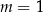 D)
D) 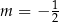
Jeżeli wykres funkcji 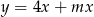 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 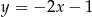 to
to
A) 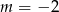 B)
B) 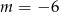 C)
C) 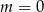 D)
D) 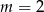
Wykres funkcji kwadratowej 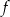 ma dwa punkty wspólne z osią
ma dwa punkty wspólne z osią 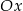 . Wskaż wzór tej funkcji
. Wskaż wzór tej funkcji
A) 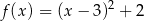 B)
B) 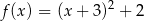
C) 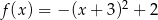 D)
D) 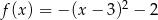
Wykres funkcji kwadratowej 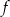 ma dwa punkty wspólne z osią
ma dwa punkty wspólne z osią 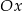 . Wskaż wzór tej funkcji
. Wskaż wzór tej funkcji
A) 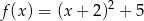 B)
B) 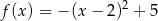
C) 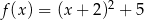 D)
D) 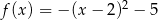
Wykres funkcji kwadratowej  ma dwa punkty wspólne z osią
ma dwa punkty wspólne z osią 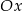 . Wskaż wzór tej funkcji
. Wskaż wzór tej funkcji
A) 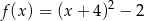 B)
B) 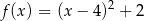
C) 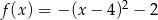 D)
D) 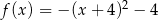
W kartezjańskim układzie współrzędnych  narysowano wykres funkcji
narysowano wykres funkcji 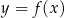 (zobacz rysunek).
(zobacz rysunek).
Funkcja  jest rosnąca w zbiorze
jest rosnąca w zbiorze
A) ![[− 2,0]](https://img.zadania.info/zad/3267981/HzadT4x.png) B)
B) ![[− 1 ,1 ]](https://img.zadania.info/zad/3267981/HzadT5x.png) C)
C) ![(2,3]](https://img.zadania.info/zad/3267981/HzadT6x.png) D)
D) ![[− 1,2 ]](https://img.zadania.info/zad/3267981/HzadT7x.png)
Jaki jest wzór funkcji kwadratowej, której wykres przedstawiono na rysunku?
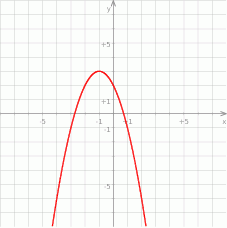
A) 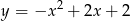 B)
B) 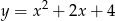 C)
C) 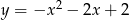 D)
D) 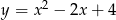
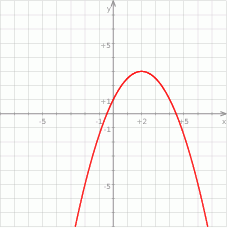
Wzorem funkcji kwadratowej 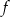 , której fragment wykresu przedstawiono na rysunku jest:
, której fragment wykresu przedstawiono na rysunku jest:
A) 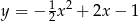 B)
B) 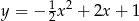 C)
C) 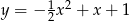 D)
D) 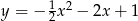
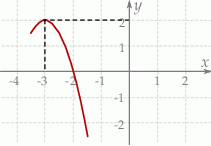
Dany jest fragment wykresu pewnej funkcji kwadratowej 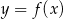 . Funkcja ta ma wzór
. Funkcja ta ma wzór
A) 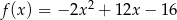 B)
B) 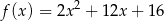
C) 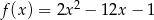 D)
D) 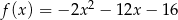
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 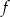 .
.
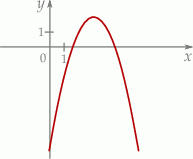
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji  .
.
A) 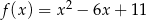 B)
B) 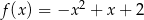
C) 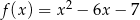 D)
D) 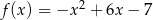
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 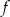 .
.
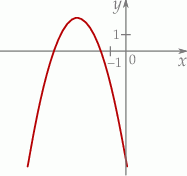
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji  .
.
A) 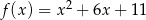 B)
B) 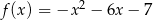
C) 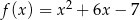 D)
D) 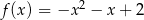
Jaki jest wzór funkcji kwadratowej, której wykres przedstawiono na rysunku?
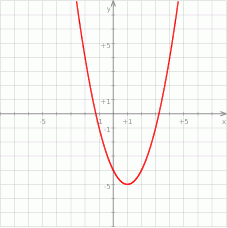
A) 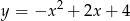 B)
B) 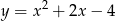 C)
C) 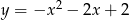 D)
D) 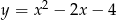
Wierzchołek paraboli będącej wykresem funkcji kwadratowej 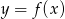 ma współrzędne
ma współrzędne 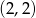 . Wówczas wierzchołek paraboli będącej wykresem funkcji
. Wówczas wierzchołek paraboli będącej wykresem funkcji 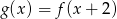 ma współrzędne
ma współrzędne
A) 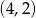 B)
B) 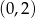 C)
C) 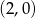 D)
D) 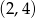
Wierzchołek paraboli będącej wykresem funkcji kwadratowej 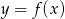 ma współrzędne
ma współrzędne 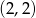 . Wówczas wierzchołek paraboli będącej wykresem funkcji
. Wówczas wierzchołek paraboli będącej wykresem funkcji 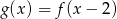 ma współrzędne
ma współrzędne
A) 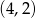 B)
B) 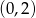 C)
C) 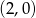 D)
D) 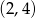
Rysunek przedstawia wykres funkcji 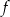 zbudowany z 6 odcinków, przy czym punkty
zbudowany z 6 odcinków, przy czym punkty 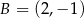 i
i 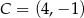 należą do wykresu funkcji.
należą do wykresu funkcji.
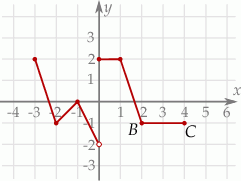
Równanie 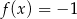 ma
ma
A) dokładnie jedno rozwiązanie. B) dokładnie dwa rozwiązania.
C) dokładnie trzy rozwiązania. D) nieskończenie wiele rozwiązań.
Na rysunku jest przedstawiony fragment wykresu funkcji 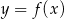 .
.
W przedziale 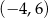 równanie
równanie 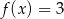
A) nie ma rozwiązań.
B) ma dokładnie dwa rozwiązania.
C) ma dokładnie trzy rozwiązania.
D) ma nieskończenie wiele rozwiązań.
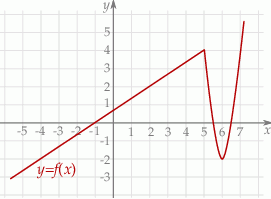
Na rysunku jest przedstawiony fragment wykresu funkcji 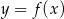 .
.
W przedziale 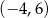 równanie
równanie 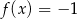
A) nie ma rozwiązań.
B) ma dokładnie dwa rozwiązania.
C) ma dokładnie trzy rozwiązania.
D) ma nieskończenie wiele rozwiązań.
Rysunek przedstawia wykres funkcji  określonej dla
określonej dla 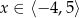 .
.
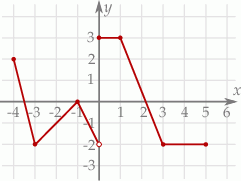
Równanie 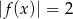 ma
ma
A) dokładnie dwa rozwiązania. B) dokładnie cztery rozwiązania.
C) dokładnie pięć rozwiązań. D) nieskończenie wiele rozwiązań.
Rysunek przedstawia wykres funkcji 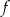 zbudowany z 6 odcinków.
zbudowany z 6 odcinków.
Równanie 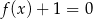 ma
ma
A) dokładnie jedno rozwiązanie. B) dokładnie dwa rozwiązania.
C) dokładnie trzy rozwiązania. D) nieskończenie wiele rozwiązań.
Wykres funkcji liniowej 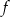 jest prostopadły do prostej
jest prostopadły do prostej 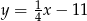 i przechodzi przez punkt
i przechodzi przez punkt 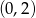 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 2 B) -8 C) 0,5 D) -0,5
Wykres funkcji liniowej 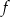 jest prostopadły do prostej
jest prostopadły do prostej 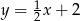 i przechodzi przez punkt
i przechodzi przez punkt  . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 2 B) -8 C) 1 D) -1
Wykres funkcji liniowej  jest prostopadły do prostej
jest prostopadły do prostej 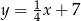 i przechodzi przez punkt
i przechodzi przez punkt 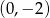 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 2 B) -8 C) 0,5 D) -0,5
Zbiorem wartości funkcji 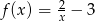 jest
jest
A) 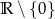 B)
B) 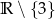 C)
C) 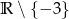 D)
D) 
Zbiorem wartości funkcji 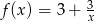 jest
jest
A) 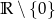 B)
B) 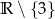 C)
C) 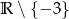 D)
D) 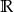
Zbiorem wartości funkcji 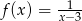 jest
jest
A) 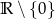 B)
B) 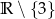 C)
C) 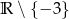 D)
D) 
Wierzchołek paraboli o równaniu 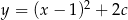 leży na prostej o równaniu
leży na prostej o równaniu 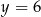 . Wtedy
. Wtedy
A) 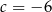 B)
B) 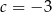 C)
C) 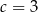 D)
D) 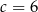
Wierzchołek paraboli o równaniu 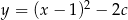 leży na prostej o równaniu
leży na prostej o równaniu 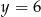 . Wtedy
. Wtedy
A) 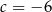 B)
B) 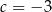 C)
C) 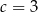 D)
D) 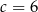
Jeśli wiadomo, że wierzchołek funkcji 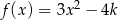 należy do prostej
należy do prostej 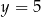 , to wartość liczbowa współczynnika
, to wartość liczbowa współczynnika 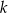 jest równa
jest równa
A) 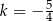 B)
B) 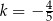 C)
C) 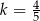 D)
D) 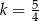
Wierzchołek paraboli o równaniu 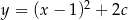 leży na prostej o równaniu
leży na prostej o równaniu 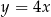 . Wtedy
. Wtedy
A) 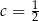 B)
B) 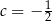 C)
C) 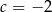 D)
D) 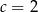
Wierzchołek paraboli o równaniu 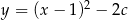 leży na prostej o równaniu
leży na prostej o równaniu 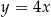 . Wtedy
. Wtedy
A) 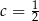 B)
B) 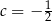 C)
C) 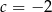 D)
D) 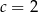
Wykresem funkcji kwadratowej 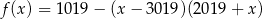 jest parabola, której wierzchołek leży na prostej
jest parabola, której wierzchołek leży na prostej
A) 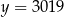 B)
B) 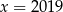 C)
C) 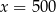 D)
D)