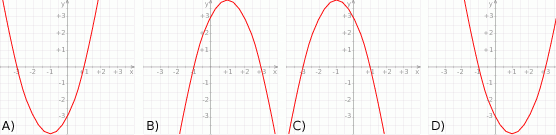
Wierzchołek paraboli 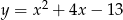 leży na prostej o równaniu
leży na prostej o równaniu
A) 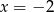 B)
B) 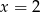 C)
C) 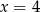 D)
D) 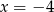
/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Parabola
Wierzchołek paraboli 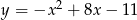 leży na prostej o równaniu
leży na prostej o równaniu
A) 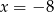 B)
B) 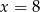 C)
C) 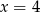 D)
D) 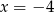
Wierzchołek paraboli 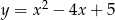 leży na prostej o równaniu
leży na prostej o równaniu
A) 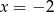 B)
B) 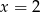 C)
C) 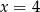 D)
D) 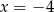
Wykresem funkcji kwadratowej 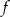 jest parabola o wierzchołku
jest parabola o wierzchołku 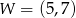 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 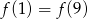 B)
B) 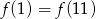 C)
C) 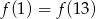 D)
D) 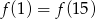
Wykresem funkcji kwadratowej 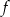 jest parabola o wierzchołku
jest parabola o wierzchołku 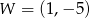 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 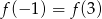 B)
B) 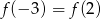 C)
C) 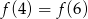 D)
D) 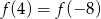
Wykresem funkcji kwadratowej 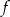 jest parabola o wierzchołku
jest parabola o wierzchołku 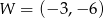 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 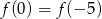 B)
B) 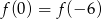 C)
C) 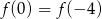 D)
D) 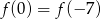
Wykresem funkcji kwadratowej 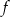 jest parabola o wierzchołku
jest parabola o wierzchołku 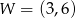 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 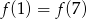 B)
B) 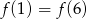 C)
C) 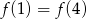 D)
D) 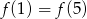
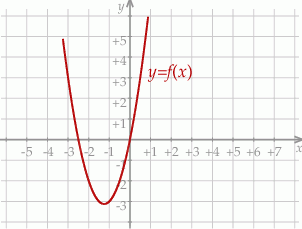
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 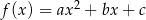 , której miejsca zerowe to:
, której miejsca zerowe to: 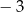 i 2. Do wykresu tego należy punkt
i 2. Do wykresu tego należy punkt 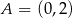 .
.
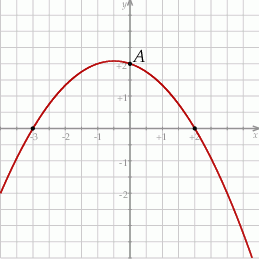
Współczynnik  we wzorze funkcji
we wzorze funkcji 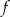 jest równy
jest równy
A) 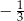 B)
B) 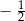 C)
C) 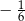 D)
D) 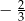
Punkty 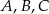 są punktami przecięcia paraboli o równaniu
są punktami przecięcia paraboli o równaniu 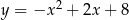 z osiami układu współrzędnych. Pole trójkąta
z osiami układu współrzędnych. Pole trójkąta 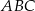 jest równe
jest równe
A) 8 B) 9 C) 24 D) 27
Punkt 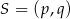 jest wierzchołkiem paraboli będącej wykresem funkcji
jest wierzchołkiem paraboli będącej wykresem funkcji 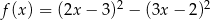 . Zatem
. Zatem
A) 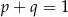 B)
B) 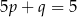 C)
C) 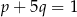 D)
D) 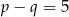
Ile punktów wspólnych z osią 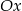 ma wykres funkcji kwadratowej
ma wykres funkcji kwadratowej 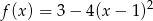 ?
?
A) 0 B) 1 C) 2 D) 3
Ile punktów wspólnych z osią 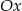 ma wykres funkcji kwadratowej
ma wykres funkcji kwadratowej 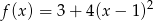 ?
?
A) 0 B) 1 C) 2 D) 3
Ile punktów wspólnych z osią 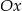 ma wykres funkcji kwadratowej
ma wykres funkcji kwadratowej 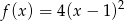 ?
?
A) 0 B) 1 C) 2 D) 3
Funkcja kwadratowa 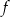 jest określona wzorem
jest określona wzorem 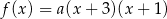 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 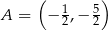 .
.
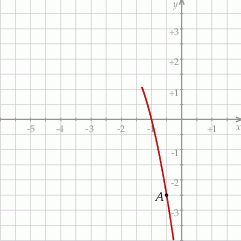
Najmniejsza wartość funkcji 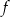 w przedziale
w przedziale 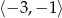 jest równa
jest równa
A) 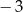 B) 0 C)
B) 0 C) 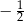 D)
D) 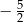
Wykresem funkcji kwadratowej 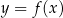 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 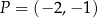 . Prosta
. Prosta 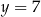 przecina tę parabolę w punktach
przecina tę parabolę w punktach 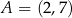 i
i 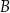 . Długość odcinka
. Długość odcinka 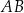 jest równa
jest równa
A) 18 B) 6 C) 10 D) 8
Funkcja kwadratowa 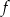 jest określona wzorem
jest określona wzorem 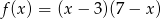 . Wierzchołek paraboli będącej wykresem funkcji
. Wierzchołek paraboli będącej wykresem funkcji 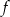 należy do prostej o równaniu
należy do prostej o równaniu
A) 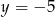 B)
B) 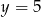 C)
C) 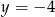 D)
D) 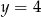
Funkcja kwadratowa 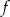 jest określona wzorem
jest określona wzorem 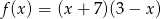 . Wierzchołek paraboli będącej wykresem funkcji
. Wierzchołek paraboli będącej wykresem funkcji 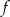 należy do prostej o równaniu
należy do prostej o równaniu
A) 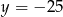 B)
B) 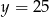 C)
C) 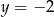 D)
D) 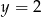
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 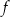 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 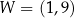 . Liczby
. Liczby 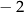 i 4 to miejsca zerowe funkcji
i 4 to miejsca zerowe funkcji 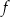 .
.
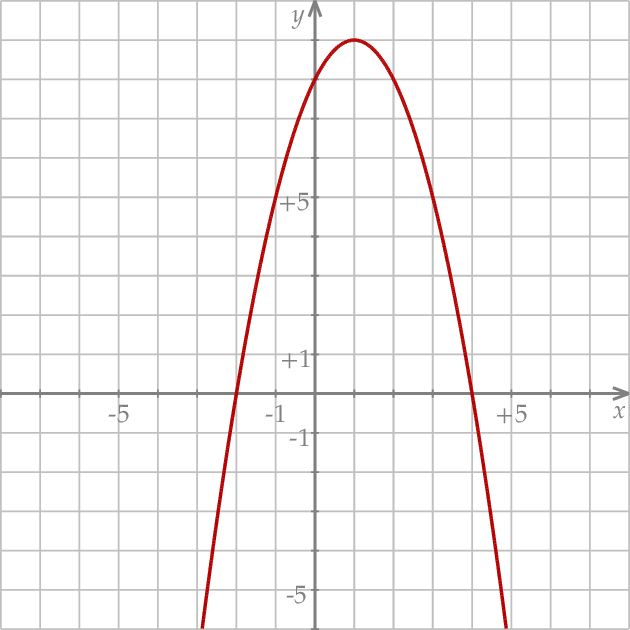
Najmniejsza wartość funkcji 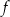 w przedziale
w przedziale 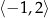 jest równa
jest równa
A) 2 B) 5 C) 8 D) 9
Funkcja kwadratowa 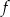 jest określona wzorem
jest określona wzorem 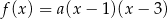 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 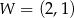 .
.
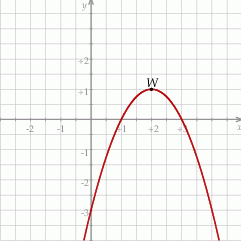
Największa wartość funkcji 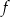 w przedziale
w przedziale 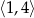 jest równa
jest równa
A) 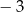 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 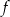 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 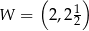 . Liczby
. Liczby 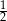 i
i 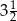 to miejsca zerowe funkcji
to miejsca zerowe funkcji 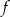 .
.
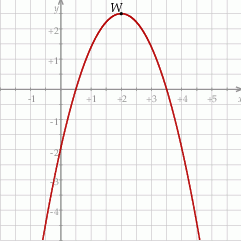
Najmniejsza wartość funkcji 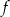 w przedziale
w przedziale 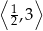 jest równa
jest równa
A) 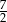 B)
B) 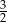 C) 0 D)
C) 0 D) 
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 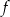 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 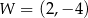 . Liczby 0 i 4 to miejsca zerowe funkcji
. Liczby 0 i 4 to miejsca zerowe funkcji 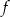 .
.
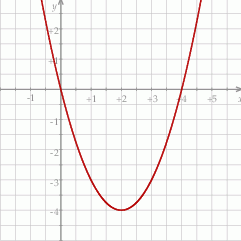
Największa wartość funkcji 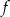 w przedziale
w przedziale 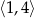 jest równa
jest równa
A) 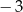 B)
B) 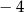 C) 4 D) 0
C) 4 D) 0
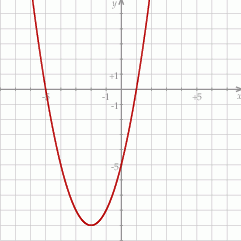
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 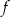 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 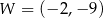 . Liczby
. Liczby 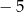 i 1 to miejsca zerowe funkcji
i 1 to miejsca zerowe funkcji 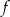 .
.
Największa wartość funkcji 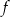 w przedziale
w przedziale 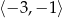 jest równa
jest równa
A) 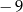 B)
B) 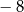 C)
C) 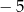 D) 0
D) 0
Funkcja kwadratowa 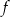 jest określona wzorem
jest określona wzorem 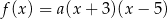 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 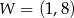 .
.
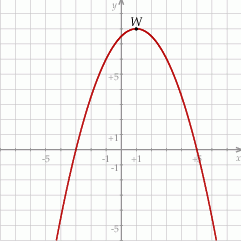
Największa wartość funkcji 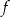 w przedziale
w przedziale 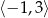 jest równa
jest równa
A) 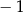 B) 0 C) 8 D) 6
B) 0 C) 8 D) 6
Punkt 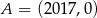 należy do wykresu funkcji
należy do wykresu funkcji 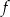 określonej wzorem
określonej wzorem
A) 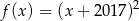 B)
B) 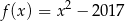
C) 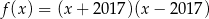 D)
D) 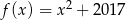
Punkt 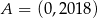 należy do wykresu funkcji
należy do wykresu funkcji 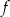 określonej wzorem
określonej wzorem
A) 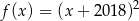 B)
B) 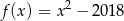
C) 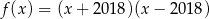 D)
D) 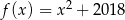
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 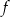 określonej wzorem
określonej wzorem 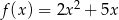 .
.
Osią symetrii wykresu funkcji
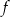 jest prosta o równaniu
jest prosta o równaniu A)
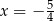 B)
B) 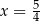 C)
C) 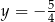 D)
D) 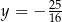
Funkcja kwadratowa 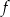 jest określona wzorem
jest określona wzorem 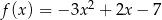 . Jeżeli przesuniemy wykres funkcji
. Jeżeli przesuniemy wykres funkcji 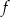 o dwie jednostki 2 lewo, to otrzymamy wykres funkcji
o dwie jednostki 2 lewo, to otrzymamy wykres funkcji
A) 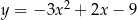 B)
B) 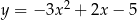
C) 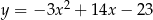 D)
D) 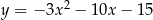
Odległość wierzchołka paraboli 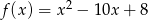 od osi
od osi 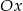 jest równa
jest równa
A) 5 B) 17 C) 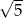 D)
D) 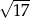
Odległość wierzchołka paraboli 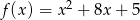 od osi
od osi 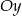 jest równa
jest równa
A) -11 B) 11 C) 4 D) 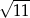
Odległość wierzchołka paraboli 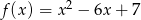 od osi
od osi 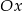 jest równa
jest równa
A) 2 B) -2 C) 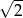 D) 3
D) 3
Wykres funkcji kwadratowej 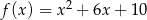 powstaje z wykresu funkcji
powstaje z wykresu funkcji 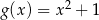 przez przesunięcie o 3 jednostki
przez przesunięcie o 3 jednostki
A) w prawo B) w lewo C) w górę D) w dół
Wykres funkcji kwadratowej 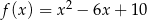 powstaje z wykresu funkcji
powstaje z wykresu funkcji 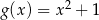 przez przesunięcie o 3 jednostki
przez przesunięcie o 3 jednostki
A) w prawo B) w lewo C) w górę D) w dół
W kartezjańskim układzie współrzędnych 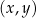 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 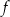 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
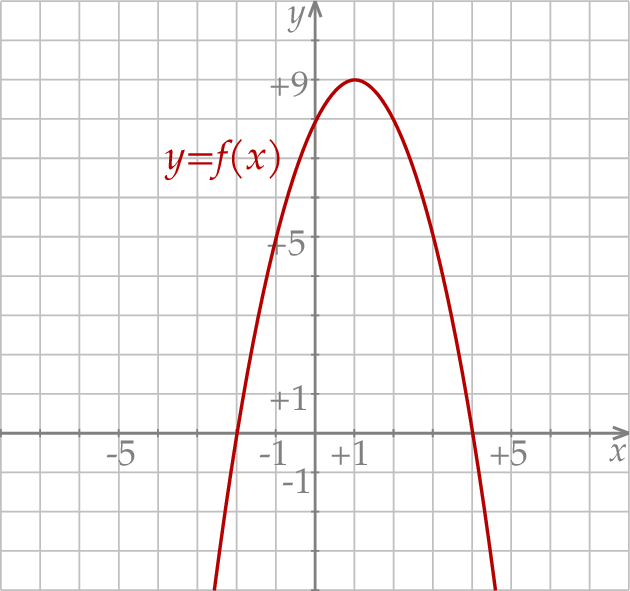
Dla funkcji 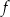 prawdziwa jest równość
prawdziwa jest równość
A) 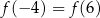 B)
B) 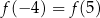 C)
C) 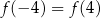 D)
D) 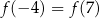
Wierzchołek 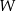 paraboli, będącej wykresem funkcji
paraboli, będącej wykresem funkcji 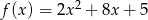 przesunięto o wektor
przesunięto o wektor 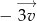 , gdzie
, gdzie ![→ v = [− 4;5]](https://img.zadania.info/zad/6882016/HzadT3x.gif) , otrzymując punkt
, otrzymując punkt 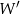 . Współrzędne punktu
. Współrzędne punktu 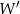 są równe
są równe
A) 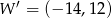 B)
B) 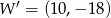 C)
C) 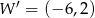 D)
D) 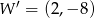
Wskaż wzór funkcji, która przecina osie układu współrzędnych w 3 punktach.
A) 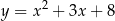 B)
B) 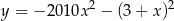
C) 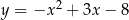 D)
D) 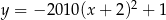
Wskaż wzór funkcji, która przecina osie układu współrzędnych w 3 punktach.
A) 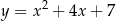 B)
B) 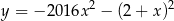
C) 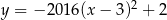 D)
D) 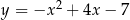
Funkcja kwadratowa 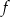 określona jest wzorem
określona jest wzorem 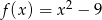 . Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą
. Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą 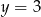 , należy go przesunąć o
, należy go przesunąć o
A) 12 jednostek w prawo wzdłuż osi 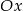
B) 12 jednostek do góry wzdłuż osi 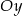
C) 12 jednostek do dołu wzdłuż osi 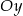
D) 3 jednostki w lewo wzdłuż osi 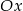
Funkcja kwadratowa 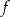 określona jest wzorem
określona jest wzorem 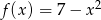 . Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą
. Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą 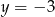 , należy go przesunąć o
, należy go przesunąć o
A) 4 jednostki do góry wzdłuż osi 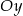
B) 10 jednostek do góry wzdłuż osi 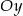
C) 4 jednostki w dół wzdłuż osi 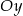
D) 10 jednostek w dół wzdłuż osi 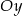
Funkcja kwadratowa 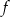 określona jest wzorem
określona jest wzorem 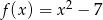 . Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą
. Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą 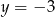 , należy go przesunąć o
, należy go przesunąć o
A) 4 jednostki do góry wzdłuż osi 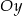
B) 10 jednostek do góry wzdłuż osi 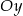
C) 4 jednostki w dół wzdłuż osi 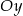
D) 10 jednostek w dół wzdłuż osi 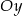
Na jednym z poniższych rysunków przedstawiono fragment wykresu funkcji 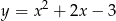 . Wskaż ten rysunek.
. Wskaż ten rysunek.
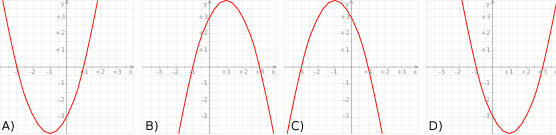
Na jednym z poniższych rysunków przedstawiono fragment wykresu funkcji 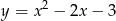 . Wskaż ten rysunek.
. Wskaż ten rysunek.