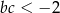Wierzchołek paraboli będącej wykresem funkcji 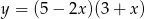 ma współrzędne
ma współrzędne
A) 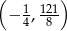 B)
B) 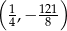 C)
C) 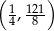 D)
D) 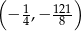
/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Parabola
Wierzchołek paraboli będącej wykresem funkcji 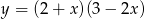 ma współrzędne
ma współrzędne
A) 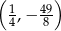 B)
B) 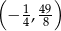 C)
C) 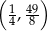 D)
D) 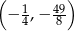
Wykresem funkcji 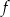 danej wzorem
danej wzorem 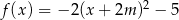 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 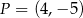 . Wówczas
. Wówczas
A) 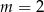 B)
B) 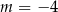 C)
C) 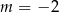 D)
D) 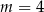
Zbiorem wartości funkcji kwadratowej 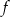 jest przedział
jest przedział 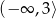 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 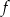 ?
?
Wskaż fragment wykresu funkcji kwadratowej, której zbiorem wartości jest  .
.
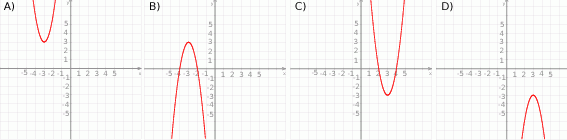
Zbiorem wartości funkcji kwadratowej 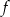 jest przedział
jest przedział 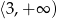 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 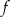 ?
?
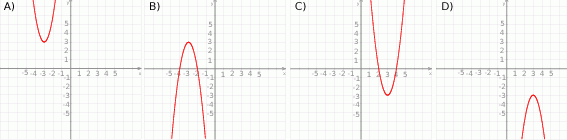
Zbiorem wartości funkcji kwadratowej 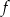 jest przedział
jest przedział 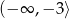 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 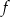 ?
?
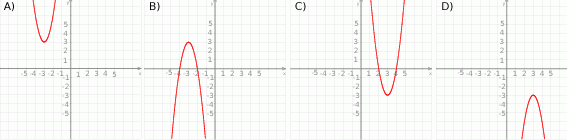
Zbiorem wartości funkcji kwadratowej 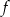 jest przedział
jest przedział 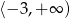 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 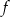 ?
?
Osią symetrii paraboli będącej wykresem funkcji 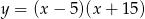 jest prosta o równaniu
jest prosta o równaniu
A) 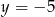 B)
B) 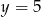 C)
C) 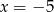 D)
D) 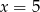
Osią symetrii paraboli będącej wykresem funkcji 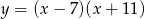 jest prosta o równaniu
jest prosta o równaniu
A) 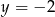 B)
B) 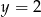 C)
C) 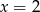 D)
D) 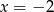
Osią symetrii paraboli określonej wzorem 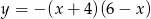 jest prosta o równaniu
jest prosta o równaniu
A) 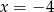 B)
B) 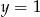 C)
C) 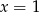 D)
D) 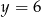
Oś symetrii paraboli, która jest wykresem funkcji 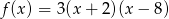 ma równanie
ma równanie
A) 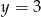 B)
B) 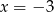 C)
C) 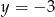 D)
D) 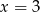
Wykresem funkcji kwadratowej 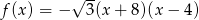 jest parabola której oś symetrii ma równanie
jest parabola której oś symetrii ma równanie
A) 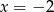 B)
B) 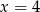 C)
C) 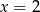 D)
D) 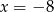
Wykresem funkcji kwadratowej 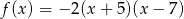 jest parabola której oś symetrii ma równanie
jest parabola której oś symetrii ma równanie
A) 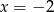 B)
B) 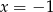 C)
C) 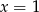 D)
D) 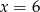
Pole figury ograniczonej fragmentem wykresu funkcji 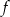 danej wzorem
danej wzorem 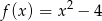 i osią
i osią 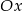 jest
jest
A) mniejsze od 8 B) większe od 8 C) równe 8 D) większe od 16
Pole figury ograniczonej fragmentem wykresu funkcji 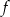 danej wzorem
danej wzorem 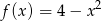 i osią
i osią 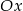 jest
jest
A) mniejsze od 16 B) mniejsze od 8 C) równe 16 D) większe od 16
Pole figury ograniczonej fragmentem wykresu funkcji 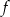 danej wzorem
danej wzorem 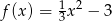 i osią
i osią 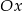 jest
jest
A) mniejsze od 9 B) równe 18 C) większe od 9 D) większe od 18
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 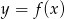 .
.
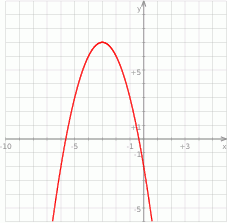
Zbiorem wartości funkcji 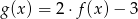 jest przedział
jest przedział
A) 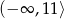 B)
B) 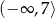 C)
C) 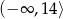 D)
D) 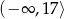
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej  . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 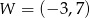 .
.
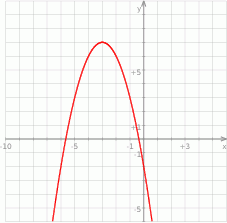
Największa wartość funkcji 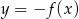 w przedziale
w przedziale 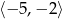 jest równa
jest równa
A)  B)
B) 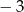 C) 7 D)
C) 7 D) 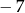
Na rysunku przedstawiono fragment paraboli będącej wykresem funkcji kwadratowej 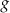 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 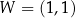 .
.
Zbiorem wartości funkcji 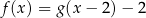 jest przedział
jest przedział
A) 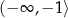 B)
B)  C)
C) 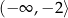 D)
D) 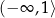
Funkcja kwadratowa 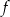 jest określona wzorem
jest określona wzorem 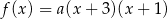 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 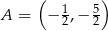 .
.
Współczynnik  we wzorze funkcji
we wzorze funkcji  jest równy
jest równy
A) 1 B) 2 C) 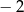 D)
D) 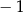
Funkcja kwadratowa 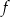 jest określona wzorem
jest określona wzorem 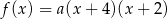 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 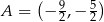 .
.
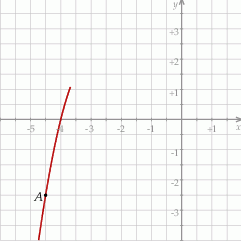
Współczynnik  we wzorze funkcji
we wzorze funkcji 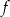 jest równy
jest równy
A) 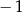 B)
B) 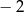 C) 2 D) 1
C) 2 D) 1
Liczba punktów wspólnych wykresu funkcji 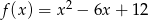 z osiami układu współrzędnych jest równa
z osiami układu współrzędnych jest równa
A) 0 B) 1 C) 2 D) 3
Liczba punktów wspólnych wykresu funkcji 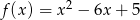 z osiami układu współrzędnych jest równa
z osiami układu współrzędnych jest równa
A) 0 B) 1 C) 2 D) 3
Pierwsza współrzędna wierzchołka paraboli o równaniu 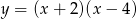 jest równa
jest równa
A) 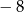 B)
B) 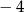 C) 1 D) 2
C) 1 D) 2
Pierwsza współrzędna wierzchołka paraboli o równaniu 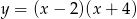 jest równa
jest równa
A) 8 B) 4 C) 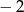 D)
D) 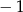
Funkcja kwadratowa 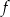 jest określona wzorem
jest określona wzorem 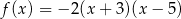 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 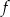 , ma współrzędną
, ma współrzędną  równą
równą
A) 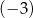 B)
B) 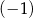 C) 1 D) 5
C) 1 D) 5
Funkcja kwadratowa 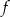 jest określona wzorem
jest określona wzorem 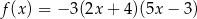 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 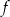 , ma współrzędną
, ma współrzędną  równą
równą
A) 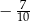 B)
B) 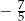 C)
C) 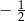 D)
D) 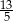
W kartezjańskim układzie współrzędnych 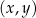 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej  (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 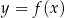 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
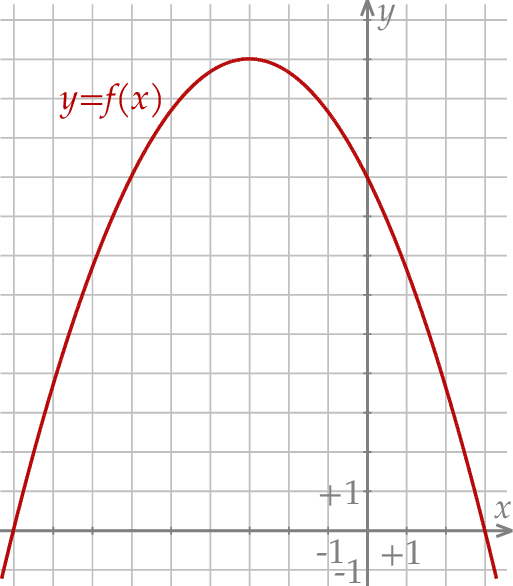
Zbiorem wartości funkcji 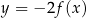 jest przedział
jest przedział
A) 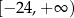 B)
B) ![(− ∞ ,12]](https://img.zadania.info/zad/9642145/HzadT6x.png) C)
C) ![(− ∞ ,− 12]](https://img.zadania.info/zad/9642145/HzadT7x.png) D)
D) 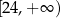
Wierzchołek paraboli 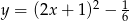 leży na prostej o równaniu
leży na prostej o równaniu
A) 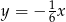 B)
B) 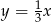 C)
C) 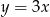 D)
D) 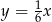
Wierzchołek paraboli 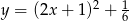 leży na prostej o równaniu
leży na prostej o równaniu
A) 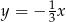 B)
B) 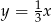 C)
C) 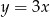 D)
D) 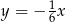
Suma odległości wierzchołka paraboli o równaniu 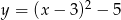 od osi układu współrzędnych jest równa
od osi układu współrzędnych jest równa
A) 4 B) 3 C) 5 D) 8
Suma odległości wierzchołka paraboli o równaniu 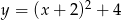 od osi układu współrzędnych jest równa
od osi układu współrzędnych jest równa
A) 6 B) 2 C) -2 D) -6
Wierzchołkiem paraboli będącej wykresem funkcji określonej wzorem 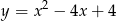 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 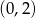 B)
B) 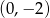 C)
C) 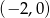 D)
D) 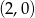
Wykresem funkcji kwadratowej 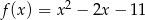 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 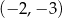 B)
B) 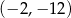 C)
C) 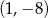 D)
D) 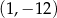
Wykresem funkcji kwadratowej 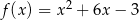 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 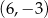 B)
B) 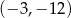 C)
C) 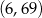 D)
D) 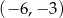
Wierzchołkiem paraboli będącej wykresem funkcji określonej wzorem 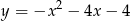 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 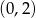 B)
B) 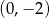 C)
C) 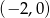 D)
D) 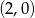
Wykresem funkcji kwadratowej 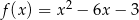 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 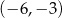 B)
B) 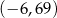 C)
C) 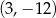 D)
D) 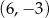
Wykresem funkcji kwadratowej 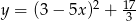 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 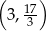 B)
B) 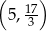 C)
C) 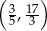 D)
D) 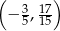
Wykresem funkcji kwadratowej 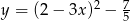 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 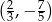 B)
B) 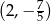 C)
C) 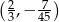 D)
D) 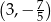
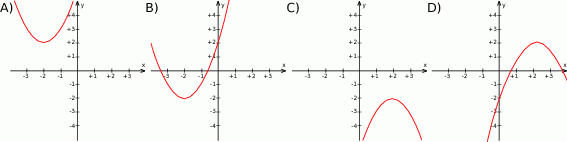
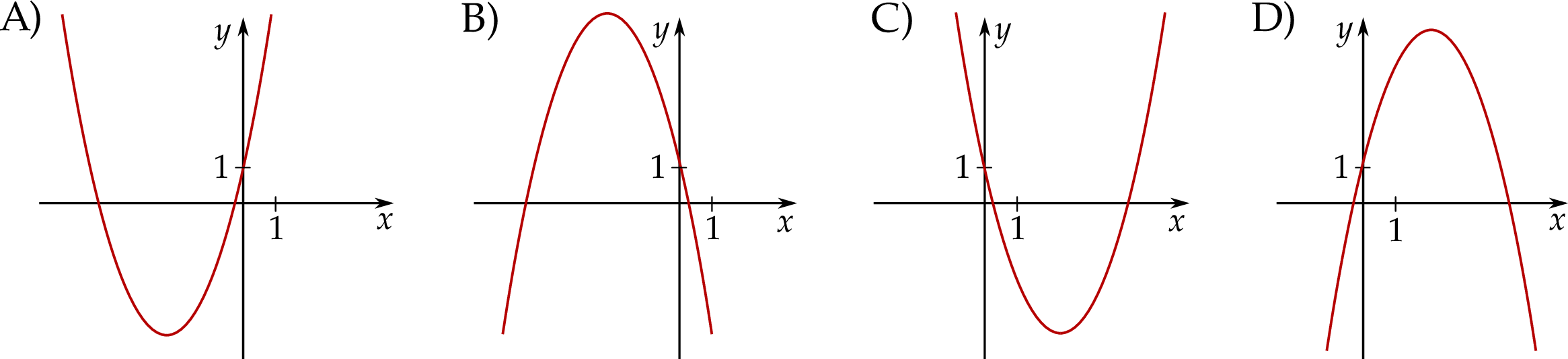
Funkcja kwadratowa 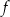 jest określona wzorem
jest określona wzorem 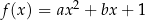 , gdzie
, gdzie  oraz
oraz 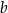 są pewnymi liczbami rzeczywistymi, takimi, że
są pewnymi liczbami rzeczywistymi, takimi, że 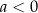 i
i 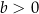 . Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych
. Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych 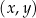 . Fragment wykresu funkcji
. Fragment wykresu funkcji  przedstawiono na rysunku
przedstawiono na rysunku
Funkcja kwadratowa  jest określona wzorem
jest określona wzorem  , gdzie
, gdzie  oraz
oraz 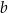 są pewnymi liczbami rzeczywistymi, takimi, że
są pewnymi liczbami rzeczywistymi, takimi, że 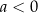 i
i 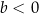 . Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych
. Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych 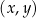 . Fragment wykresu funkcji
. Fragment wykresu funkcji 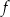 przedstawiono na rysunku
przedstawiono na rysunku
Prosta  ma dwa punkty wspólne z parabolą
ma dwa punkty wspólne z parabolą 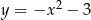 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
A) 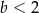 B)
B) 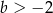 C)
C) 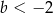 D)
D) 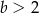
Funkcja kwadratowa 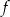 jest określona wzorem
jest określona wzorem 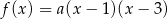 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 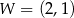 .
.
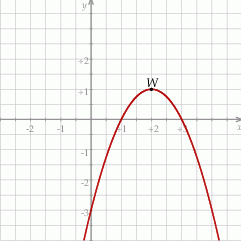
Współczynnik  we wzorze funkcji
we wzorze funkcji 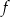 jest równy
jest równy
A) 1 B) 2 C) 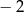 D)
D) 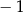
Funkcja kwadratowa 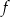 jest określona wzorem
jest określona wzorem 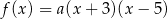 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 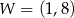 .
.
Współczynnik  we wzorze funkcji
we wzorze funkcji 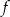 jest równy
jest równy
A) 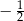 B) 2 C)
B) 2 C) 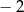 D)
D) 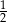
Wykres funkcji 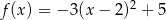 przesunięto o 3 jednostki w lewo i 2 jednostki w górę. W wyniku tej operacji otrzymano wykres funkcji
przesunięto o 3 jednostki w lewo i 2 jednostki w górę. W wyniku tej operacji otrzymano wykres funkcji
A) 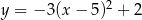 B)
B) 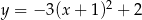
C) 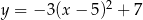 D)
D) 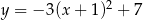
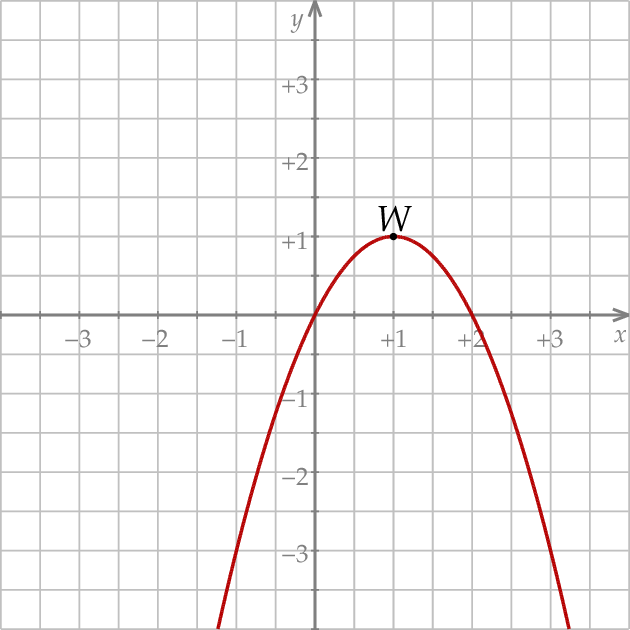
Wykres funkcji 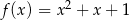 przesunięto o 2 jednostki w prawo i 1 jednostkę w górę. W wyniku tej operacji otrzymano wykres funkcji
przesunięto o 2 jednostki w prawo i 1 jednostkę w górę. W wyniku tej operacji otrzymano wykres funkcji
A) 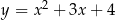 B)
B) 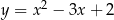
C) 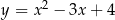 D)
D) 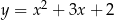
Na rysunku poniżej przedstawiono fragment wykresu funkcji kwadratowej 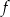 określonej wzorem
określonej wzorem 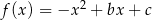 . Wierzchołek paraboli będącej wykresem tej funkcji ma współrzędne
. Wierzchołek paraboli będącej wykresem tej funkcji ma współrzędne 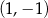 .
.
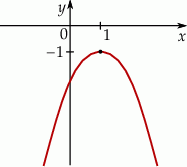
Stąd wynika, że:
A) 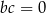 B)
B) 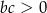 C)
C) 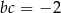 D)
D)