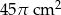Dane są dwa sześciany. Pole powierzchni całkowitej pierwszego sześcianu jest większe od pola powierzchni całkowitej drugiego sześcianu o 30%. Wynika stąd, że objętość pierwszego sześcianu jest większa od objętości drugiego sześcianu
A) o mniej niż 50%, ale więcej niż 40%. B) o mniej niż 60% , ale więcej niż 50%.
C) o mniej niż 70% , ale więcej niż 60%. D) o więcej niż 70%.
/Szkoła średnia/Zadania testowe/Geometria
Jeśli przyprostokątne trójkąta prostokątnego są równe 6 i 3, a najmniejszy kąt ma miarę  , to wyrażenie
, to wyrażenie 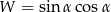 ma wartość
ma wartość
A) 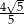 B)
B) 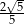 C)
C)  D)
D) 
W trójkącie prostokątnym o przyprostokątnych długości 1 i 2 kąty ostre są równe  i
i 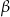 (
(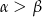 ). Wartość wyrażenia
). Wartość wyrażenia 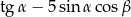 jest równe
jest równe
A) 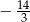 B) -2 C) 0 D)
B) -2 C) 0 D) 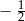
Punkty 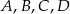 dzielą okrąg o środku
dzielą okrąg o środku 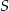 w stosunku
w stosunku 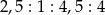 .
.
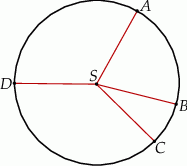
Różnica miar kątów wypukłych 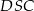 i
i 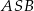 jest równa
jest równa
A) 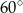 B)
B) 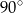 C)
C) 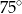 D)
D) 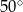
Dany jest trójkąt o bokach długości 4, 5 oraz 6. Cosinus największego kąta wewnętrznego tego trójkąta jest równy
A) 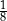 B)
B) 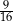 C)
C)  D)
D) 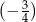
Jeżeli kąt ostry  jest o
jest o 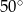 mniejszy od kąta przyległego do niego, to
mniejszy od kąta przyległego do niego, to
A) 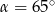 B)
B) 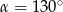 C)
C) 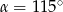 D)
D) 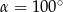
Jeżeli kąt ostry  jest o
jest o 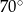 mniejszy od kąta przyległego do niego, to
mniejszy od kąta przyległego do niego, to
A) 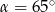 B)
B) 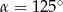 C)
C) 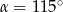 D)
D) 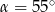
Jeżeli kąt ostry  jest o
jest o 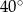 mniejszy od kąta przyległego do niego, to
mniejszy od kąta przyległego do niego, to
A) 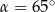 B)
B) 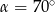 C)
C) 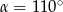 D)
D) 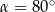
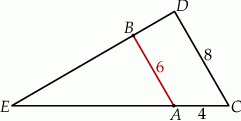
Oblicz długość odcinka 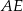 wiedząc, że
wiedząc, że 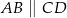 i
i 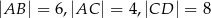 .
.
A) 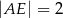 B)
B) 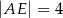 C)
C) 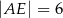 D)
D) 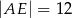
Odcinki 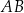 i
i 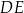 są równoległe. Długości odcinków
są równoległe. Długości odcinków 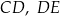 i
i 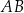 są odpowiednio równe 1, 3 i 9.
są odpowiednio równe 1, 3 i 9.
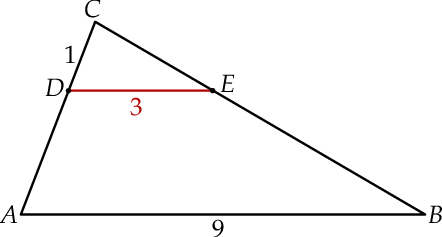
Długość odcinka 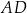 jest równa
jest równa
A) 2 B) 3 C) 5 D) 6
Odcinki 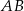 i
i 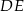 są równoległe. Długości odcinków
są równoległe. Długości odcinków 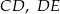 i
i 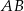 są odpowiednio równe 2, 4 i 16.
są odpowiednio równe 2, 4 i 16.
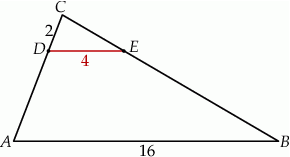
Długość odcinka 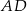 jest równa
jest równa
A) 12 B) 8 C) 3 D) 6
Odcinki 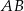 i
i 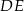 są równoległe. Długości odcinków
są równoległe. Długości odcinków 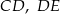 i
i  są odpowiednio równe 2, 5 i 15.
są odpowiednio równe 2, 5 i 15.
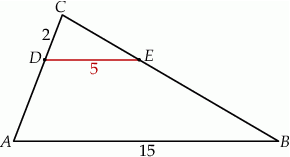
Długość odcinka  jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Jeżeli odcinki  i
i  są równoległe, to długość odcinka
są równoległe, to długość odcinka  (patrz rys.) jest równa
(patrz rys.) jest równa
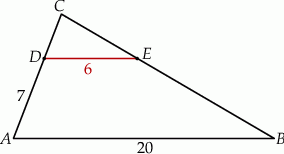
A) 9 B) 10 C) 11 D) 12
Oblicz długość odcinka  wiedząc, że
wiedząc, że 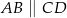 i
i 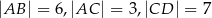 .
.
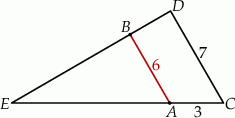
A) 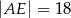 B)
B) 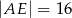 C)
C) 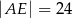 D)
D) 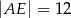
Oblicz długość odcinka 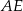 wiedząc, że
wiedząc, że 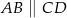 i
i 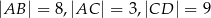 .
.
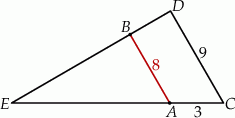
A) 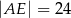 B)
B) 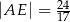 C)
C) 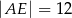 D)
D) 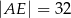
W trójkącie 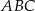 punkt
punkt 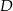 leży na boku
leży na boku 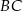 , a punkt
, a punkt 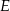 leży na boku
leży na boku 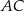 . Odcinek
. Odcinek 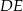 jest równoległy do boku
jest równoległy do boku 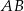 , a ponadto
, a ponadto 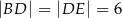 ,
, 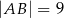 (zobacz rysunek).
(zobacz rysunek).
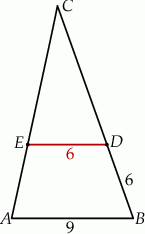
Odcinek  ma długość
ma długość
A) 8 B) 4 C) 9 D) 12
W trójkącie  punkt
punkt  leży na boku
leży na boku 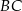 , a punkt
, a punkt 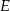 leży na boku
leży na boku 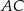 . Odcinek
. Odcinek 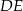 jest równoległy do boku
jest równoległy do boku 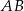 , a ponadto
, a ponadto 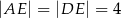 ,
, 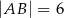 (zobacz rysunek).
(zobacz rysunek).
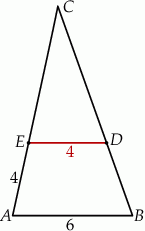
Odcinek 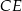 ma długość
ma długość
A) 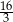 B)
B)  C) 8 D) 6
C) 8 D) 6
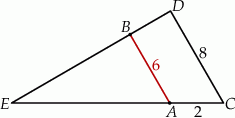
Oblicz długość odcinka 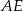 wiedząc, że
wiedząc, że 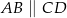 i
i 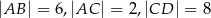 .
.
A) 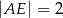 B)
B) 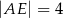 C)
C) 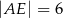 D)
D) 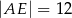
W trójkącie 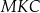 bok
bok 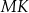 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 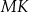 przecina boki
przecina boki 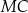 i
i 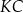 – odpowiednio – w punktach
– odpowiednio – w punktach 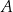 oraz
oraz 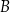 takich, że
takich, że 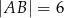 i
i 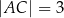 (zobacz rysunek).
(zobacz rysunek).

Długość odcinka 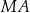 jest równa
jest równa
A) 18 B) 15 C) 9 D) 12
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 2 (zobacz rysunek).
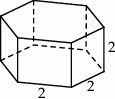
Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 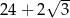 B)
B) 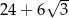 C)
C) 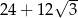 D)
D) 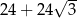
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 3 (zobacz rysunek).
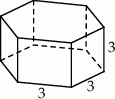
Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 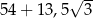 B)
B) 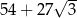 C)
C) 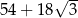 D)
D) 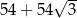
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6. Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 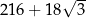 B)
B) 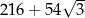 C)
C) 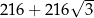 D)
D) 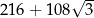
Suma długości wszystkich krawędzi sześcianu jest równa 24. Objętość tego sześcianu jest równa
A) 8 B) 27 C) 24 D) 64
Suma wszystkich krawędzi sześcianu jest równa 36. Objętość tego sześcianu jest równa
A) 8 B) 27 C) 64 D) 24
Suma długości wszystkich krawędzi sześcianu jest równa 72. Objętość tego sześcianu jest równa
A) 1728 B) 216 C) 127 D) 81
Cosinus kąta dwuściennego utworzonego przez dwie sąsiednie ściany czworościanu foremnego jest równy
A) 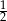 B)
B) 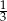 C)
C)  D)
D) 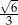
W czworościanie foremnym cosinus kąta dwuściennego między dwiema sąsiednimi ścianami jest równy
A) 0 B) 0,25 C) 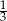 D)
D) 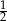
Wysokości 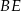 i
i 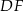 rombu
rombu 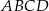 przecinają się w punkcie
przecinają się w punkcie 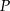 (zobacz rysunek).
(zobacz rysunek).
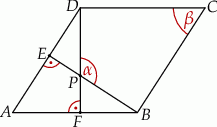
Wyrażenie 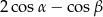 jest równe
jest równe
A) 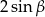 B)
B) 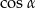 C) 0 D)
C) 0 D) 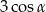
Przekrojem osiowym stożka o objętości 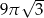 jest trójkąt równoboczny. Obwód tego trójkąta jest równy
jest trójkąt równoboczny. Obwód tego trójkąta jest równy
A) 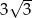 B)
B) 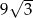 C) 18 D) 6
C) 18 D) 6
Przekrojem prostopadłościanu zawierającym przekątną podstawy i przekątne sąsiednich ścian bocznych wychodzących z tego samego wierzchołka jest
A) kwadrat B) prostokąt C) trójkąt D) trapez
Prostokąt 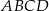 o przekątnej długości
o przekątnej długości 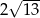 jest podobny do prostokąta o bokach długości 2 i 3. Obwód prostokąta
jest podobny do prostokąta o bokach długości 2 i 3. Obwód prostokąta 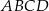 jest równy
jest równy
A) 10 B) 20 C) 5 D) 24
Prostokąt 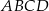 o przekątnej długości
o przekątnej długości 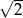 jest podobny do prostokąta o bokach długości 1 i 7. Obwód prostokąta
jest podobny do prostokąta o bokach długości 1 i 7. Obwód prostokąta 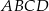 jest równy
jest równy
A) 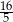 B)
B) 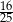 C) 80 D) 16
C) 80 D) 16
Prostokąt o bokach 4 i 6 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 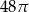 B)
B) 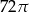 C)
C) 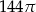 D)
D) 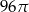
Prostokąt o bokach 10 i 6 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 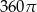 B)
B) 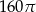 C)
C) 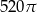 D)
D) 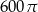
Prostokąt o bokach 3 i 5 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 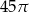 B)
B) 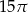 C)
C) 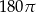 D)
D) 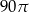
Która z liczb nie może być równa polu rombu o obwodzie 12?
A) 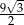 B)
B) 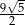 C)
C) 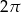 D)
D) 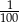
Która z liczb nie może być równa polu rombu o obwodzie 8?
A) 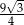 B)
B) 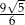 C)
C) 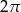 D)
D) 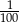
Objętość sześcianu 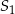 jest równa
jest równa 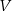 , a objętość sześcianu
, a objętość sześcianu 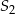 jest równa
jest równa 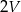 . Pole powierzchni całkowitej sześcianu
. Pole powierzchni całkowitej sześcianu 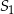 jest równe
jest równe 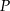 . Pole powierzchni całkowitej sześcianu
. Pole powierzchni całkowitej sześcianu 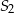 jest równe
jest równe
A) 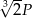 , , | B) 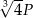 , , |
| ponieważ stosunek pól powierzchni brył podobnych jest równy | |
| 1) | sześcianowi skali podobieństwa. |
| 2) | skali podobieństwa. |
| 3) | kwadratowi skali podobieństwa. |
W trójkącie równoramiennym miara kąta przy podstawie jest równa 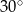 , a ramię ma długość 8 cm. Podstawa tego trójkąta ma długość
, a ramię ma długość 8 cm. Podstawa tego trójkąta ma długość
A) 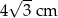 B) 4 cm C)
B) 4 cm C) 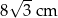 D)
D) 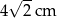
Ramię trójkąta równoramiennego ma długość 12 i tworzy z podstawą kąt o mierze 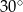 . Obwód tego trójkąta jest równy:
. Obwód tego trójkąta jest równy:
A) 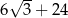 B) 30 C) 36 D)
B) 30 C) 36 D) 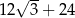
Punkt 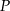 jest punktem wspólnym środkowych
jest punktem wspólnym środkowych 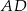 i
i 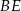 w trójkącie
w trójkącie 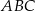 . Wówczas odcinki
. Wówczas odcinki 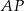 i
i 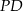 mogą mieć długości
mogą mieć długości
A) 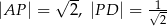 B)
B) 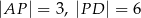
C) 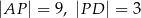 D)
D) 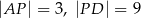
Dane są punkty 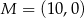 ,
, 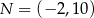 oraz
oraz 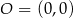 . Tangens kąta rozwartego
. Tangens kąta rozwartego 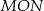 jest równy
jest równy
A) 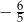 B)
B) 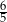 C) 1 D)
C) 1 D) 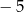
Obwód podstawy stożka wynosi 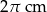 . Tworząca stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego stożka jest równe
. Tworząca stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego stożka jest równe
A) 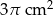 B)
B) 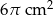 C)
C) 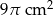 D)
D) 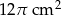
Obwód podstawy stożka wynosi 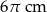 . Tworząca stożka jest 4 razy dłuższa od jego promienia podstawy. Zatem pole powierzchni całkowitej tego stożka jest równe
. Tworząca stożka jest 4 razy dłuższa od jego promienia podstawy. Zatem pole powierzchni całkowitej tego stożka jest równe
A) 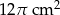 B)
B) 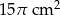 C)
C) 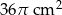 D)
D)