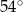Pole trójkąta przedstawionego na rysunku jest równe
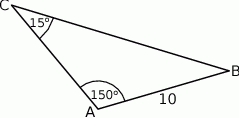
A) 50 B) 25 C) 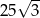 D)
D) 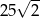
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Pole trójkąta przedstawionego na rysunku jest równe

A) 50 B) 25 C) 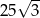 D)
D) 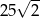
W trójkącie równoramiennym 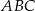 o podstawie
o podstawie 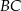 dane są:
dane są: 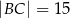 oraz
oraz 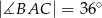 . Odcinek
. Odcinek 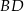 jest odcinkiem dwusiecznej kąta
jest odcinkiem dwusiecznej kąta 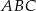 (zobacz rysunek).
(zobacz rysunek).
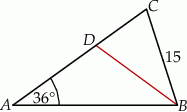
Wówczas długość odcinka 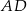 jest równa
jest równa
A) 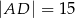 B)
B) 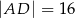 C)
C) 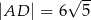 D)
D) 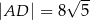
Z odcinków o długościach: 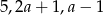 można zbudować trójkąt równoramienny. Wynika stąd, że
można zbudować trójkąt równoramienny. Wynika stąd, że
A) 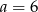 B)
B) 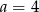 C)
C) 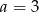 D)
D) 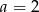
Z odcinków o długościach: 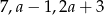 można zbudować trójkąt równoramienny. Wynika stąd, że
można zbudować trójkąt równoramienny. Wynika stąd, że
A) 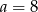 B)
B) 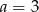 C)
C) 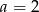 D)
D) 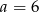
Z odcinków 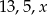 budujemy trójkąt. Będzie on prostokątny, gdy:
budujemy trójkąt. Będzie on prostokątny, gdy:
A) 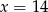 B)
B) 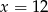 C)
C) 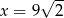 D)
D) 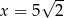
W pewnym trójkącie równoramiennym największy kąt ma miarę 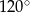 , a najdłuższy bok ma długość 12 (zobacz rysunek).
, a najdłuższy bok ma długość 12 (zobacz rysunek).
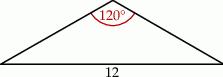
Najkrótsza wysokość tego trójkąta ma długość równą
A) 6 B) 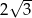 C)
C) 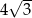 D)
D) 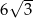
W pewnym trójkącie równoramiennym największy kąt ma miarę 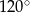 , a ramię ma długość 6 (zobacz rysunek).
, a ramię ma długość 6 (zobacz rysunek).

Najkrótsza wysokość tego trójkąta ma długość równą
A) 4 B) 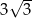 C)
C) 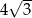 D) 3
D) 3
Ile wynosi tangens kąta  zaznaczonego na rysunku poniżej?
zaznaczonego na rysunku poniżej?
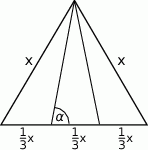
A) 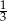 B)
B) 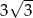 C)
C) 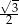 D)
D) 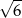
Trójkąt prostokątny równoramienny 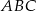 , w którym przeciwprostokątna jest równa
, w którym przeciwprostokątna jest równa 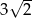 , jest podobny do trójkąta
, jest podobny do trójkąta 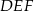 w skali
w skali 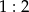 . Obwód trójkąta
. Obwód trójkąta 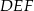 jest równy
jest równy
A) 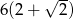 B)
B) 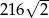 C)
C) 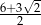 D)
D) 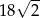
Trójkąt prostokątny równoramienny 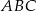 , w którym przeciwprostokątna jest równa
, w którym przeciwprostokątna jest równa 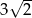 , jest podobny do trójkąta
, jest podobny do trójkąta 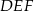 w skali
w skali 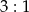 . Obwód trójkąta
. Obwód trójkąta 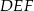 jest równy
jest równy
A) 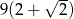 B)
B) 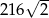 C)
C) 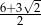 D)
D) 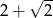
Trójkąt prostokątny równoramienny 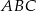 , w którym przeciwprostokątna jest równa
, w którym przeciwprostokątna jest równa 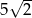 , jest podobny do trójkąta
, jest podobny do trójkąta 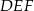 w skali
w skali 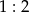 . Obwód trójkąta
. Obwód trójkąta 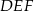 jest równy
jest równy
A) 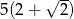 B)
B) 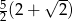 C)
C) 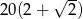 D)
D) 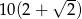
Pole trójkąta o bokach 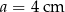 i
i 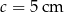 oraz kącie
oraz kącie 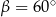 zawartym między danymi bokami jest równe
zawartym między danymi bokami jest równe
A) 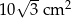 B)
B) 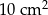 C)
C) 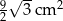 D)
D) 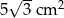
Pole trójkąta o bokach długości 4 oraz 9 i kącie między nimi o mierze 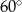 jest równe
jest równe
A) 18 B) 9 C) 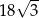 D)
D) 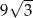
Długości boków trójkąta wynoszą 2 i 8, zaś kąt między nimi zawarty ma miarę 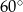 . Pole tego trójkąta wynosi
. Pole tego trójkąta wynosi
A) 8 B) 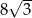 C) 4 D)
C) 4 D) 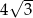
Dany jest trójkąt 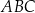 , w którym
, w którym 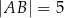 ,
, 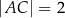 oraz
oraz 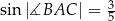 . Pole trójkąta
. Pole trójkąta 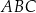 jest równe
jest równe
A) 3 B) 5 C) 6 D) 10
Pole trójkąta o bokach 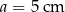 i
i 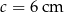 oraz kącie
oraz kącie 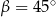 zawartym między danymi bokami jest równe
zawartym między danymi bokami jest równe
A) 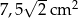 B)
B) 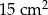 C)
C) 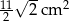 D)
D) 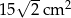
Ile wynosi pole trójkąta, w którym dwa boki mają długości 7 i 12, a kąt zawarty między nimi wynosi 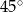 ?
?
A) 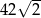 B) 42 C)
B) 42 C) 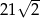 D) 21
D) 21
Wysokość w trójkącie prostokątnym dzieli podstawę na odcinki o długościach 3 i 5. Pole tego trójkąta jest równe:
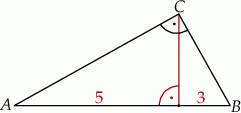
A) 15 B) 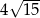 C) 16 D) za mało danych
C) 16 D) za mało danych
Liczby naturalne 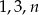 są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
A) 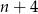 B)
B) 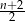 C)
C)  D) 3
D) 3
Liczby naturalne 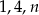 są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
A) 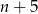 B)
B) 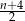 C) 4 D)
C) 4 D) 
Jeśli trójkąt prostokątny jest wpisany w okrąg o promieniu 6, a jednym z jego kątów ostrych jest kąt 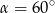 , to pole tego trójkąta jest równe
, to pole tego trójkąta jest równe
A) 36 B) 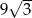 C) 18 D)
C) 18 D) 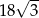
Jeśli trójkąt prostokątny jest wpisany w okrąg o promieniu 4, a jednym z jego kątów ostrych jest kąt 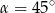 , to pole tego trójkąta jest równe
, to pole tego trójkąta jest równe
A) 16 B) 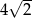 C) 8 D)
C) 8 D) 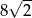
Jeśli trójkąt prostokątny jest wpisany w okrąg o promieniu 4, a jednym z jego kątów ostrych jest kąt 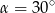 , to pole tego trójkąta jest równe
, to pole tego trójkąta jest równe
A) 16 B) 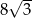 C) 8 D)
C) 8 D) 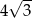
Jedna z przyprostokątnych trójkąta prostokątnego jest 3 razy dłuższa od drugiej. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 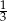 B) 3 C)
B) 3 C) 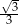 D)
D) 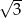
Jedna z przyprostokątnych trójkąta prostokątnego jest 5 razy krótsza od drugiej. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 5 B) 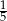 C)
C) 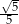 D)
D) 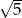
W trójkącie prostokątnym o bokach 6, 8, 10, tangens najmniejszego kąta jest równy:
A)  B)
B) 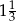 C)
C)  D)
D) 
Przyprostokątne trójkąta prostokątnego mają długość 3 i 4. Wynika stąd, że tangens mniejszego z kątów ostrych jest równy
A)  B)
B)  C)
C) 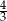 D)
D) 
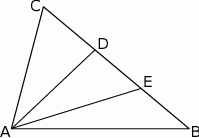
Punkty 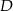 i
i 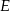 dzielą bok
dzielą bok 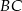 trójkąta
trójkąta 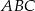 na trzy odcinki, których stosunek długości
na trzy odcinki, których stosunek długości 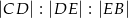 jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów
jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów 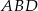 i
i 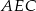 jest równy
jest równy
A)  B)
B) 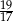 C)
C) 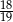 D)
D) 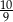
Jeżeli wysokość trójkąta równobocznego wynosi 2, to długość jego boku jest równa
A) 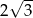 B)
B) 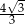 C)
C) 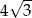 D) 6
D) 6
W trójkącie równobocznym wysokość jest równa 12. Zatem bok tego trójkąta ma długość
A) 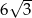 B)
B) 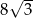 C) 24 D) 8
C) 24 D) 8
Jeżeli wysokość trójkąta równobocznego wynosi 3, to długość jego boku jest równa
A) 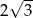 B)
B) 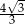 C)
C) 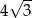 D) 6
D) 6
Jeżeli wysokość trójkąta równobocznego wynosi 6, to długość jego boku jest równa
A) 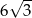 B)
B) 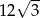 C)
C) 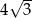 D) 18
D) 18
Jeżeli wysokość trójkąta równobocznego wynosi 4, to długość jego boku jest równa
A) 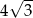 B)
B) 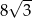 C)
C) 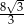 D) 12
D) 12
Długość boku trójkąta równobocznego o wysokości 6 cm jest równa:
A) 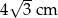 B) 12 cm C)
B) 12 cm C) 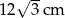 D)
D) 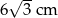
W trójkącie równoramiennym 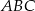 poprowadzono wysokość
poprowadzono wysokość 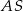 , która utworzyła z podstawą kąt o mierze
, która utworzyła z podstawą kąt o mierze 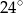 (zobacz rysunek). Ramię tego trójkąta ma długość 10. Długość wysokości
(zobacz rysunek). Ramię tego trójkąta ma długość 10. Długość wysokości 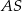 jest liczbą z przedziału
jest liczbą z przedziału
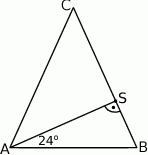
A) 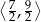 B)
B) 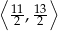 C)
C) 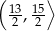 D)
D) 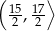
Jeśli jeden bok trójkąta ma długość 3 a drugi 5, to długość trzeciego boku nie może być równa
A) 9 B) 7 C) 6 D) 5
Długości boków trójkąta nie mogą być równe:
A) 3, 4, 4 B) 3, 4, 5 C) 3, 4, 2 D) 3, 4, 8
Dany jest trójkąt równoramienny 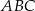 , w którym
, w którym 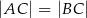 . Dwusieczna kąta poprowadzona z wierzchołka
. Dwusieczna kąta poprowadzona z wierzchołka 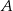 przecina bok
przecina bok 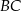 tego trójkąta w punkcie
tego trójkąta w punkcie 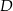 . Kąt
. Kąt 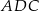 ma miarę
ma miarę 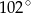 . Kąt między ramionami tego trójkąta ma miarę
. Kąt między ramionami tego trójkąta ma miarę
A) 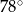 B)
B) 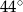 C)
C) 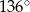 D)
D) 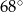
Punkt 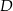 jest środkiem podstawy trójkąta równoramiennego
jest środkiem podstawy trójkąta równoramiennego 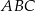 , w którym
, w którym 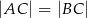 . Odległość punktu
. Odległość punktu 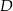 od prostej
od prostej 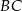 jest równa 12, a długość odcinka
jest równa 12, a długość odcinka 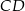 jest równa 20.
jest równa 20.
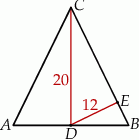
Podstawa 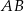 trójkąta
trójkąta 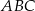 ma długość
ma długość
A) 15 B) 30 C) 24 D) 16
Wierzchołki trójkąta 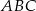 leżą na okręgu o środku
leżą na okręgu o środku 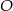 .
. 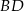 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 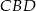 ma miarę
ma miarę 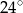 , to kąt
, to kąt 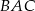 ma miarę
ma miarę
A) 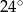 B)
B) 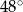 C)
C) 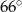 D)
D) 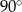
Wierzchołki trójkąta 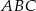 leżą na okręgu o środku
leżą na okręgu o środku 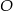 .
. 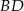 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 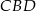 ma miarę
ma miarę 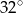 , to kąt
, to kąt 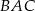 ma miarę
ma miarę
A) 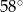 B)
B) 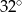 C)
C) 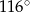 D)
D) 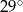
Wierzchołki trójkąta 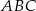 leżą na okręgu o środku
leżą na okręgu o środku 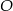 .
. 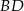 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 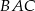 ma miarę
ma miarę 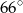 , to kąt
, to kąt 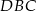 ma miarę
ma miarę
A) 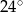 B)
B) 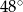 C)
C) 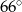 D)
D) 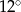
Punkty 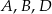 leżą na jednej prostej. Odcinek
leżą na jednej prostej. Odcinek 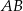 jest podstawą trójkąta równoramiennego
jest podstawą trójkąta równoramiennego  (zobacz rysunek).
(zobacz rysunek).
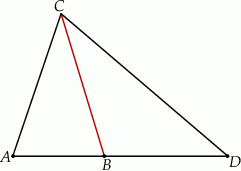
Jeżeli 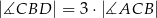 , to
, to 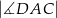 wynosi
wynosi
A) 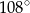 B)
B) 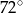 C)
C) 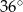 D)
D)