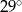Punkty 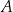 ,
, 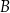 oraz
oraz 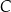 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 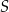 . Długość łuku
. Długość łuku 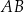 , na którym jest oparty kąt wpisany
, na którym jest oparty kąt wpisany 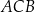 , jest równa
, jest równa 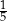 długości okręgu.
długości okręgu.

Miara kąta ostrego 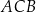 jest równa
jest równa
A) 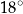 B)
B) 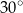 C)
C) 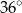 D)
D) 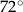
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkty 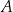 ,
, 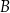 oraz
oraz 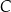 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 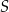 . Długość łuku
. Długość łuku 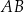 , na którym jest oparty kąt wpisany
, na którym jest oparty kąt wpisany 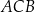 , jest równa
, jest równa 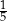 długości okręgu.
długości okręgu.

Miara kąta ostrego 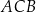 jest równa
jest równa
A) 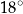 B)
B) 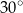 C)
C) 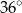 D)
D) 
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 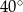 B)
B) 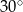 C)
C) 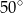 D)
D) 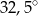
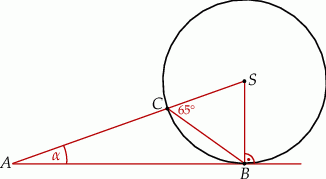
Prosta 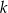 jest styczna w punkcie
jest styczna w punkcie 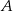 do okręgu o środku
do okręgu o środku 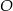 . Punkt
. Punkt 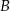 leży na tym okręgu i miara kąta
leży na tym okręgu i miara kąta 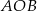 jest równa
jest równa 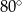 . Przez punkty
. Przez punkty 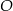 i
i 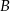 poprowadzono prostą, która przecina prostą
poprowadzono prostą, która przecina prostą 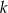 w punkcie
w punkcie 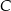 (zobacz rysunek).
(zobacz rysunek).

Miara kąta 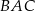 jest równa
jest równa
A) 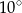 B)
B) 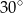 C)
C) 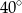 D)
D) 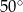
Prosta 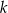 jest styczna w punkcie
jest styczna w punkcie 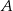 do okręgu o środku
do okręgu o środku 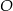 . Punkt
. Punkt 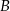 leży na tym okręgu i miara kąta
leży na tym okręgu i miara kąta 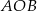 jest równa
jest równa 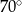 . Przez punkty
. Przez punkty 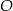 i
i 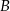 poprowadzono prostą, która przecina prostą
poprowadzono prostą, która przecina prostą 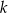 w punkcie
w punkcie 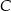 (zobacz rysunek).
(zobacz rysunek).
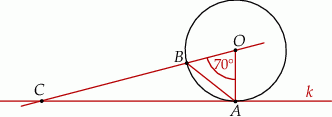
Miara kąta 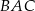 jest równa
jest równa
A) 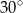 B)
B) 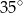 C)
C) 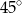 D)
D) 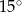
Odcinek 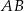 jest średnicą okręgu o środku
jest średnicą okręgu o środku 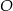 i promieniu
i promieniu  . Na tym okręgu wybrano punkt
. Na tym okręgu wybrano punkt 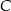 , taki, że
, taki, że 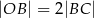 (zobacz rysunek).
(zobacz rysunek).
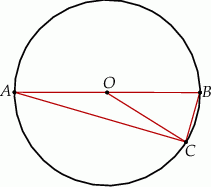
Pole trójkąta 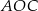 jest równe
jest równe
A) 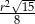 B)
B) 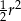 C)
C) 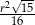 D)
D) 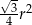
Kąt wpisany oparty na łuku okręgu długości 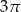 ma miarę
ma miarę 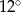 . Jakie jest pole koła ograniczonego tym okręgiem?
. Jakie jest pole koła ograniczonego tym okręgiem?
A) 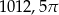 B)
B) 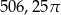 C)
C) 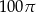 D)
D) 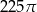
Kąt środkowy okręgu jest większy od kąta wpisanego opartego na tym samym łuku, o
A) 200% B) 150% C) 100% D) 50%
Kąt wpisany okręgu jest mniejszy od kąta środkowego opartego na tym samym łuku, o
A) 25% B) 50% C) 100% D) 150%
Odcinek 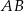 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 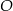 i promieniu
i promieniu 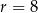 (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 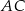 ma długość
ma długość 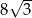 .
.
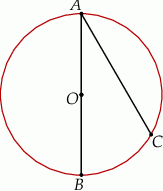
Miara kąta 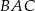 jest równa
jest równa
A) 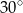 B)
B) 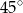 C)
C) 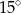 D)
D) 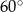
Odcinek 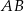 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 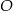 i promieniu
i promieniu 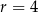 (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 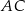 ma długość
ma długość 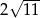 .
.
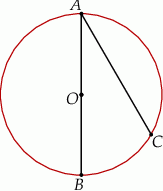
Sinus kąta 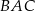 jest równy
jest równy
A) 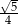 B)
B) 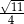 C)
C) 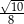 D)
D) 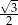
Kąt wpisany w okrąg o promieniu 10 ma miarę 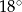 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 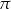 B)
B) 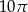 C)
C) 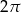 D)
D) 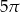
Kąt wpisany w okrąg o promieniu 8 ma miarę 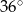 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 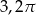 B)
B) 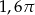 C)
C) 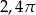 D)
D) 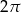
Kąt wpisany w okrąg o promieniu 9 ma miarę 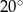 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 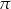 B)
B) 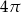 C)
C) 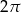 D)
D) 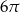
Kąt wpisany w okrąg o promieniu 9 ma miarę 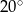 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 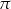 B)
B) 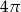 C)
C) 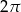 D)
D) 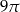
Kąt między cięciwą 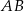 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 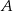 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 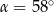 . Wówczas
. Wówczas
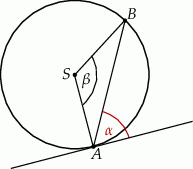
A) 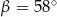 B)
B) 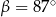 C)
C) 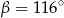 D)
D) 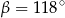
Punkty 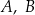 oraz
oraz 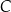 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 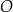 . Prosta
. Prosta 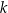 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 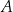 i tworzy z cięciwą
i tworzy z cięciwą 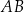 kąt o mierze
kąt o mierze 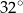 . Ponadto odcinek
. Ponadto odcinek 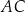 jest średnicą tego okręgu (zobacz rysunek).
jest średnicą tego okręgu (zobacz rysunek).

Miara kąta rozwartego 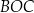 jest równa
jest równa
A) 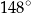 B)
B) 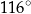 C)
C) 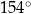 D)
D) 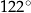
Kąt między cięciwą 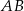 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 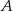 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 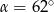 . Wówczas
. Wówczas
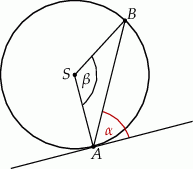
A) 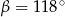 B)
B) 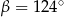 C)
C) 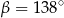 D)
D) 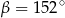
Punkty 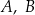 oraz
oraz 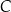 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 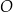 . Prosta
. Prosta 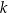 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 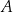 i tworzy z cięciwą
i tworzy z cięciwą 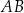 kąt o mierze
kąt o mierze 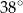 . Ponadto odcinek
. Ponadto odcinek 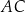 jest średnicą tego okręgu (zobacz rysunek).
jest średnicą tego okręgu (zobacz rysunek).

Miara kąta rozwartego 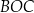 jest równa
jest równa
A) 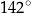 B)
B) 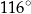 C)
C) 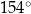 D)
D) 
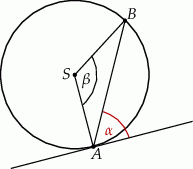
Kąt między cięciwą 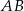 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 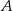 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 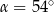 . Wówczas
. Wówczas
A) 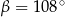 B)
B) 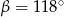 C)
C) 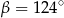 D)
D) 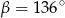
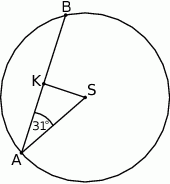
W okręgu o środku w punkcie 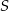 poprowadzono cięciwę
poprowadzono cięciwę 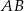 , która utworzyła z promieniem
, która utworzyła z promieniem 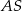 kąt o mierze
kąt o mierze 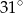 (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu
(zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu 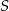 od cięciwy
od cięciwy 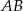 jest liczbą z przedziału
jest liczbą z przedziału
A) 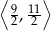 B)
B) 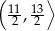 C)
C) 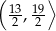 D)
D) 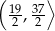
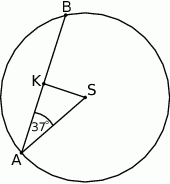
W okręgu o środku w punkcie 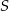 poprowadzono cięciwę
poprowadzono cięciwę 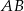 , która utworzyła z promieniem
, która utworzyła z promieniem 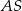 kąt o mierze
kąt o mierze 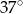 (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu
(zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu 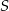 od cięciwy
od cięciwy 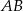 jest liczbą z przedziału
jest liczbą z przedziału
A) 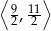 B)
B) 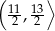 C)
C) 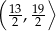 D)
D) 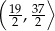
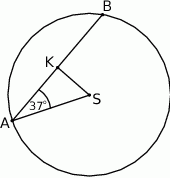
W okręgu o środku w punkcie 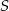 poprowadzono cięciwę
poprowadzono cięciwę 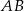 , która utworzyła z promieniem
, która utworzyła z promieniem 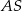 kąt o mierze
kąt o mierze 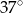 (zobacz rysunek). Promień tego okręgu ma długość 10. Długość cięciwy
(zobacz rysunek). Promień tego okręgu ma długość 10. Długość cięciwy 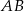 jest liczbą z przedziału
jest liczbą z przedziału
A) 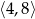 B)
B) 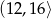 C)
C) 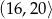 D)
D) 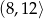
Cięciwy 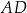 i
i 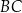 okręgu o środku
okręgu o środku 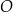 przecinają się w punkcie
przecinają się w punkcie 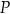 tak, że
tak, że 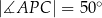 (zobacz rysunek).
(zobacz rysunek).

Jeżeli punkt 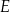 jest punktem wspólnym prostych
jest punktem wspólnym prostych 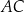 i
i 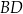 , to miara kąta
, to miara kąta 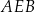 jest równa
jest równa
A) 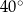 B)
B) 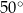 C)
C) 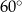 D)
D) 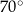
Punkty 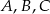 i
i 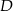 leżą na okręgu o środku
leżą na okręgu o środku 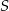 . Cięciwa
. Cięciwa 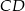 przecina średnicę
przecina średnicę 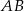 tego okręgu w punkcie
tego okręgu w punkcie 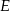 tak, że
tak, że 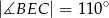 . Kąt środkowy
. Kąt środkowy 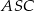 ma miarę
ma miarę 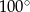 (zobacz rysunek).
(zobacz rysunek).
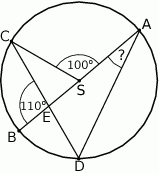
Kąt wpisany 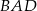 ma miarę
ma miarę
A) 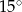 B)
B) 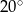 C)
C) 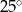 D)
D) 
Punkty 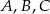 i
i 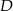 leżą na okręgu o środku
leżą na okręgu o środku 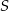 . Cięciwa
. Cięciwa 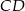 przecina średnicę
przecina średnicę 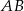 tego okręgu w punkcie
tego okręgu w punkcie 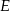 tak, że
tak, że 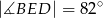 . Kąt środkowy
. Kąt środkowy 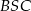 ma miarę
ma miarę 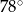 (zobacz rysunek).
(zobacz rysunek).
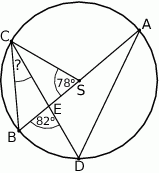
Kąt wpisany 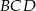 ma miarę
ma miarę
A) 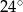 B)
B) 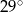 C)
C) 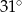 D)
D) 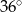
Punkty 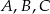 i
i 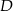 leżą na okręgu o środku
leżą na okręgu o środku 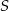 . Cięciwa
. Cięciwa 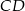 przecina średnicę
przecina średnicę 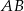 tego okręgu w punkcie
tego okręgu w punkcie 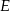 tak, że
tak, że 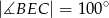 . Kąt środkowy
. Kąt środkowy 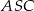 ma miarę
ma miarę 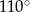 (zobacz rysunek).
(zobacz rysunek).
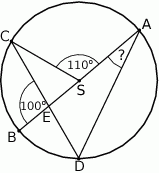
Kąt wpisany 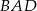 ma miarę
ma miarę
A) 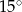 B)
B) 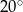 C)
C) 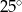 D)
D) 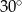
Punkty 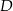 i
i 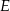 leżą na okręgu opisanym na trójkącie równobocznym
leżą na okręgu opisanym na trójkącie równobocznym 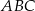 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 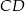 jest średnicą tego okręgu. Kąt wpisany
jest średnicą tego okręgu. Kąt wpisany 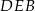 ma miarę
ma miarę  .
.
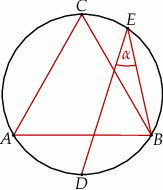
Zatem
A) 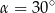 B)
B) 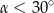 C)
C) 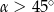 D)
D) 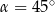
Pole pierścienia kołowego na rysunku jest równe 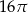 (mniejszy okrąg jest styczny do boków kwadratu
(mniejszy okrąg jest styczny do boków kwadratu 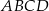 , a do większego okręgu należą punkty
, a do większego okręgu należą punkty 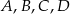 ). Zatem długość boku kwadratu
). Zatem długość boku kwadratu 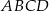 jest równa:
jest równa:
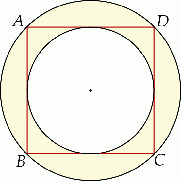
A) 2 B) 4 C) 8 D) 16
Pole pierścienia kołowego na rysunku jest równe 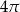 (mniejszy okrąg jest wpisany w trójkąt
(mniejszy okrąg jest wpisany w trójkąt 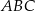 , a wierzchołki
, a wierzchołki 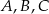 leżą na większym okręgu). Zatem długość boku trójkąta równobocznego
leżą na większym okręgu). Zatem długość boku trójkąta równobocznego 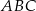 jest równa:
jest równa:
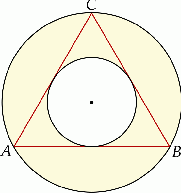
A) 2 B) 4 C) 8 D) 16
Dany jest czworokąt 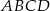 wpisany w okrąg o środku
wpisany w okrąg o środku 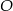 . Wówczas, jeśli
. Wówczas, jeśli 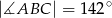 , to miara kąta
, to miara kąta 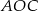 jest równa
jest równa
A) 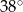 B)
B) 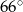 C)
C) 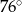 D)
D) 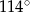
Dany jest czworokąt 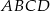 wpisany w okrąg o środku
wpisany w okrąg o środku 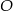 . Wówczas, jeśli
. Wówczas, jeśli 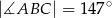 , to miara kąta
, to miara kąta 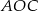 jest równa
jest równa
A) 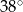 B)
B) 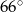 C)
C) 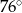 D)
D) 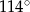
Dany jest czworokąt 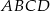 wpisany w okrąg o środku
wpisany w okrąg o środku 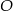 . Wówczas, jeśli
. Wówczas, jeśli 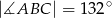 , to miara kąta
, to miara kąta 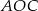 jest równa
jest równa
A) 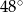 B)
B) 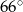 C)
C) 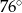 D)
D) 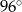
Punkty 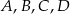 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 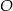 . Kąt środkowy
. Kąt środkowy 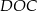 ma miarę
ma miarę 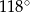 (zobacz rysunek).
(zobacz rysunek).
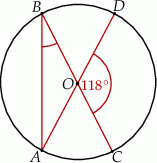
Miara kąta 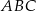 jest równa
jest równa
A) 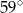 B)
B) 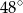 C)
C) 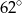 D)
D) 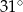
Punkty 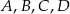 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 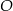 . Kąt środkowy
. Kąt środkowy 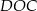 ma miarę
ma miarę 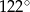 (zobacz rysunek).
(zobacz rysunek).
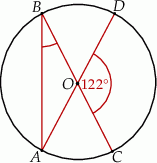
Miara kąta 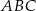 jest równa
jest równa
A) 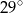 B)
B) 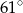 C)
C) 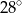 D)
D) 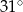
Trapez równoramienny 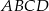 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 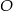 (zobacz rysunek).
(zobacz rysunek).
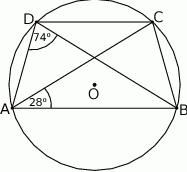
Różnica miar kątów 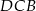 i
i 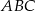 tego trapezu jest równa
tego trapezu jest równa
A) 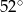 B)
B) 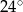 C)
C) 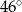 D)
D) 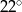
Cięciwy 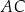 i
i 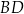 okręgu przecinają się w punkcie
okręgu przecinają się w punkcie 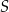 w ten sposób, że
w ten sposób, że 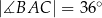 i
i 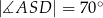 (zobacz rysunek).
(zobacz rysunek).

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 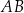 i i 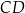 są równoległe. są równoległe. | P | F |
Trójkąty 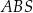 i i 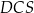 są podobne. są podobne. | P | F |
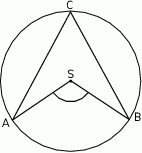
Punkt 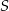 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
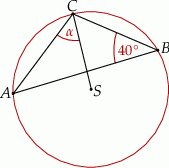
A) 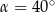 B)
B) 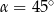 C)
C) 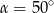 D)
D) 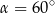
Punkt 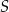 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy

A) 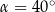 B)
B) 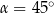 C)
C) 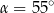 D)
D) 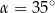
W trójkącie 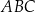 , wpisanym w okrąg o środku w punkcie
, wpisanym w okrąg o środku w punkcie 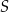 , kąt
, kąt 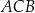 ma miarę
ma miarę 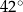 (zobacz rysunek).
(zobacz rysunek).

Miara kąta ostrego 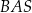 jest równa
jest równa
A) 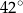 B)
B) 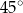 C)
C) 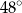 D)
D) 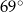
Średnice 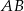 i
i 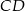 okręgu o środku
okręgu o środku 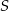 przecinają się pod kątem
przecinają się pod kątem 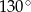 (tak jak na rysunku).
(tak jak na rysunku).
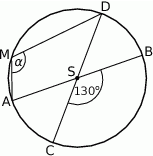
Miara kąta  jest równa
jest równa
A) 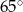 B)
B) 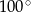 C)
C) 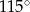 D)
D) 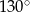
Punkt 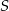 jest środkiem okręgu, na którym leżą punkty
jest środkiem okręgu, na którym leżą punkty 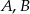 i
i 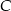 (patrz rysunek). Jeśli
(patrz rysunek). Jeśli 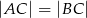 i miara kąta wypukłego
i miara kąta wypukłego 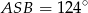 , to kąt wypukły
, to kąt wypukły 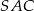 jest równy
jest równy
A) 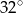 B)
B) 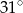 C)
C) 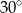 D)
D)