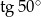Nie istnieje kąt  , taki, że
, taki, że
A) 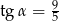 B)
B) 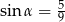 C)
C) 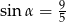 D)
D) 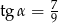
/Szkoła średnia/Zadania testowe/Funkcje/Trygonometryczna
Nie istnieje kąt  , taki, że
, taki, że
A) 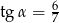 B)
B) 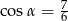 C)
C) 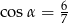 D)
D) 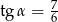
Nie istnieje kąt ostry  , taki, że
, taki, że
A) 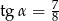 B)
B) 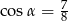 C)
C) 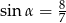 D)
D) 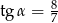
Nie istnieje kąt  , taki, że
, taki, że
A) 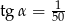 B)
B) 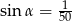 C)
C) 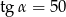 D)
D) 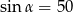
Kąt  jest ostry i
jest ostry i 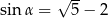 . Wartość wyrażenia
. Wartość wyrażenia 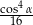 jest równa
jest równa
A) 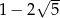 B)
B) 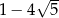 C)
C) 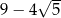 D)
D) 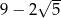
Kąt  jest ostry i
jest ostry i 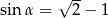 . Wartość wyrażenia
. Wartość wyrażenia 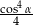 jest równa
jest równa
A) 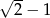 B)
B) 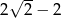 C)
C) 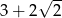 D)
D) 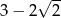
Która z liczb jest największa?
A) 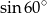 B)
B) 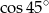 C)
C) 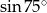 D)
D) 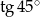
Kąt  jest ostry i
jest ostry i 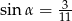 . Wówczas
. Wówczas 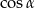 jest równy
jest równy
A) 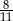 B)
B) 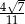 C)
C) 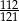 D)
D) 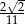
Kąt  jest ostry oraz
jest ostry oraz 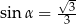 . Wtedy
. Wtedy
A) 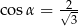 B)
B) 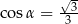 C)
C) 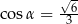 D)
D) 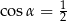
Kąt  jest ostry i
jest ostry i 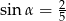 . Wówczas
. Wówczas 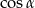 jest równy
jest równy
A)  B)
B) 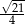 C)
C)  D)
D) 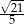
Sinusa kąta ostrego  jest równy 0,2. Cosinus kąta
jest równy 0,2. Cosinus kąta  jest równy
jest równy
A) 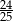 B)
B) 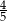 C)
C) 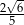 D)
D) 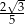
Sinus kąta ostrego  jest równy
jest równy  . Wtedy
. Wtedy
A) 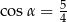 B)
B) 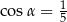 C)
C) 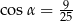 D)
D) 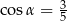
Kąt  jest ostry oraz
jest ostry oraz 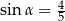 . Wtedy
. Wtedy
A) 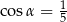 B)
B) 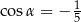 C)
C) 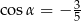 D)
D) 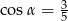
Sinus kąta ostrego  jest równy
jest równy  . Wówczas
. Wówczas
A) 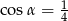 B)
B) 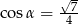 C)
C) 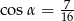 D)
D) 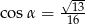
Kąt  jest ostry i spełniona jest równość
jest ostry i spełniona jest równość 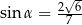 . Stąd wynika, że
. Stąd wynika, że
A) 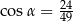 B)
B) 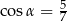 C)
C) 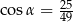 D)
D) 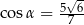
Sinus kąta ostrego  jest równy
jest równy 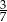 . Wówczas cosinus tego kąta jest równy
. Wówczas cosinus tego kąta jest równy
A) 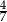 B)
B)  C)
C) 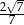 D)
D) 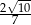
Sinus kąta ostrego  jest równy
jest równy 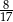 . Wówczas
. Wówczas
A) 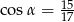 B)
B) 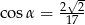 C)
C) 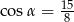 D)
D) 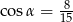
Jeśli wiadomo, że 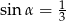 i
i  jest kątem ostrym, to prawdą jest, że
jest kątem ostrym, to prawdą jest, że
A) 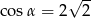 B)
B) 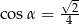 C)
C) 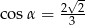 D)
D) 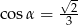
Kąt  jest ostry oraz
jest ostry oraz 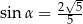 . Wtedy
. Wtedy
A) 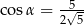 B)
B) 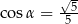 C)
C) 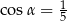 D)
D) 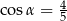
Kąt  jest ostry i
jest ostry i 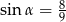 . Wówczas
. Wówczas 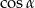 jest równy
jest równy
A) 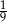 B)
B) 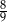 C)
C) 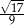 D)
D) 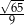
Kąt  jest ostry i
jest ostry i 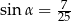 . Wynika stąd, że
. Wynika stąd, że
A) 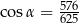 B)
B) 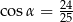 C)
C) 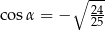 D)
D) 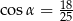
Kąt  jest ostry i
jest ostry i 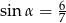 . Wówczas
. Wówczas 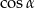 jest równy
jest równy
A) 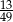 B)
B) 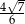 C)
C) 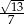 D)
D) 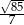
Wartość wyrażenia 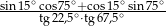 jest równa
jest równa
A) 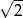 B)
B) 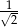 C) 1 D)
C) 1 D) 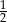
Wartość wyrażenia 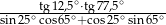 jest równa
jest równa
A) 1 B) 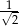 C)
C) 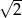 D)
D) 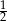
Wartość wyrażenia 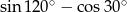 jest równa
jest równa
A) 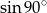 B)
B) 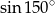 C)
C) 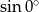 D)
D) 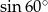
Wartość wyrażenia 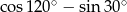 jest równa
jest równa
A) 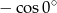 B)
B) 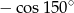 C)
C) 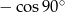 D)
D) 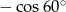
Liczba 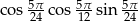 jest równa
jest równa
A) 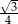 B)
B) 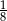 C)
C) 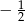 D)
D) 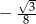
Wyrażenie 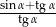 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 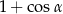 B)
B) 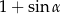 C)
C) 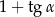 D)
D) 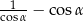
Wyrażenie 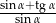 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 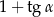 B)
B) 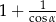 C)
C) 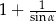 D)
D) 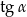
Wyrażenie 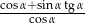 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 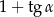 B)
B) 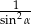 C)
C) 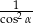 D)
D) 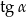
Dla ostrego kąta  wyrażenie
wyrażenie 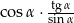 jest równe
jest równe
A) 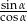 B)
B) 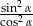 C)
C) 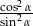 D)
D) 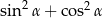
Wyrażenie 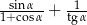 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 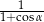 B)
B) 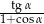 C)
C) 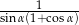 D)
D) 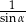
Kąt ostry  jest większy od kąta ostrego
jest większy od kąta ostrego 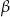 . Wynika stąd, że
. Wynika stąd, że
A) 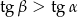 B)
B) 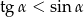 C)
C) 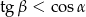 D)
D) 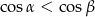
Kąt ostry  jest większy od kąta ostrego
jest większy od kąta ostrego 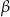 . Wynika stąd, że
. Wynika stąd, że
A) 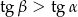 B)
B) 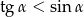 C)
C) 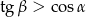 D)
D) 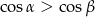
Kąt ostry  jest mniejszy od kąta ostrego
jest mniejszy od kąta ostrego 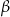 . Wynika stąd, że
. Wynika stąd, że
A) 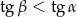 B)
B) 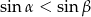 C)
C) 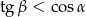 D)
D) 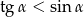
Jeśli  jest kątem ostrym i
jest kątem ostrym i  , to suma
, to suma 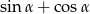 jest równa
jest równa
A) 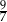 B)
B) 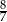 C)
C) 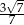 D)
D) 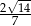
Jeśli  jest kątem ostrym i
jest kątem ostrym i 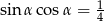 , to suma
, to suma 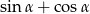 jest równa
jest równa
A) 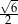 B)
B) 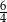 C)
C) 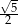 D)
D) 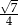
Jeśli  jest kątem ostrym i
jest kątem ostrym i 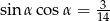 , to różnica
, to różnica 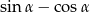 jest równa
jest równa
A) 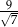 lub
lub 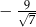
B) 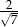 lub
lub 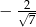
C) 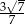 lub
lub 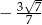
D) 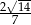 lub
lub 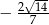
Wartość wyrażenia 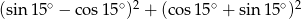 jest równa
jest równa
A) 1 B) 2 C) 0 D) 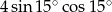
Wartość wyrażenia 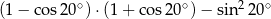 jest równa
jest równa
A) 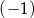 B) 0 C) 1 D) 20
B) 0 C) 1 D) 20
Wartość wyrażenia 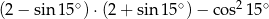 jest równa
jest równa
A) 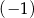 B) 3 C) 15 D) 0
B) 3 C) 15 D) 0
Wartość wyrażenia 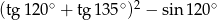 jest równa
jest równa
A) 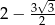 B)
B) 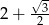 C)
C) 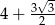 D)
D) 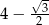
Dla pewnego kąta ostrego zachodzi 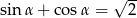 . Wtedy
. Wtedy 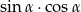 jest równy:
jest równy:
A) 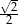 B)
B) 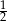 C)
C) 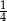 D) 1
D) 1
Kąt  jest ostry i
jest ostry i 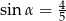 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 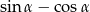 jest równa
jest równa
A) 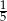 B)
B)  C)
C) 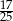 D)
D) 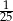
Kąt  jest ostry i
jest ostry i 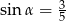 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 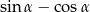 jest równa
jest równa
A) 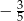 B)
B) 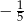 C)
C) 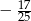 D)
D) 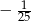
Wartość wyrażenia 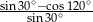 jest równa
jest równa
A) 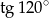 B) 2 C) 1 D)
B) 2 C) 1 D) 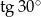
Wartość wyrażenia 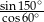 jest równa
jest równa
A) 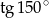 B)
B) 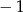 C) 1 D)
C) 1 D) 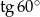
Jeśli dla kąta ostrego 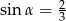 , to
, to
A) 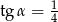 B)
B) 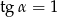 C)
C) 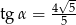 D)
D) 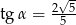
Jeśli dla kąta ostrego 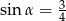 , to
, to
A) 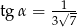 B)
B) 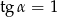 C)
C) 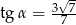 D)
D) 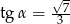
Kąt  jest ostry oraz
jest ostry oraz 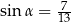 . Wtedy
. Wtedy 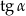 jest równy
jest równy
A)  B)
B) 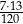 C)
C) 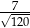 D)
D) 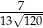
Wiadomo, że  jest kątem ostrym oraz
jest kątem ostrym oraz 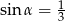 . Wówczas
. Wówczas
A) 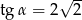 B)
B) 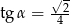 C)
C) 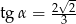 D)
D) 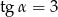
Kąt  jest kątem ostrym takim, że
jest kątem ostrym takim, że 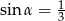 . Zatem
. Zatem
A) 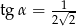 i
i 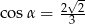
B) 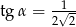 i
i 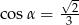
C) 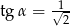 i
i 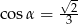
D) 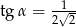 i
i 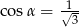
Kąt  jest ostry oraz
jest ostry oraz 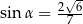 . Tangens kąta
. Tangens kąta  jest równy
jest równy
A) 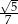 B)
B) 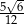 C)
C) 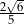 D)
D) 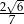
Sinus kąta ostrego  jest równy
jest równy 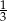 . Wówczas
. Wówczas 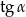 jest równy
jest równy
A) 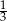 B)
B) 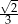 C)
C) 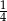 D)
D) 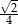
Kąt  jest ostry oraz
jest ostry oraz 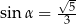 . Tangens kąta
. Tangens kąta  jest równy
jest równy
A) 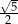 B)
B)  C)
C) 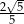 D)
D) 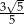
Jeśli dla kąta ostrego 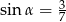 , to
, to
A) 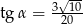 B)
B) 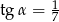 C)
C) 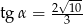 D)
D) 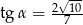
Jeżeli 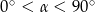 oraz
oraz 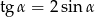 , to
, to
A) 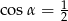 B)
B) 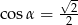 C)
C) 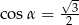 D)
D) 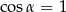
Kąt  jest ostry oraz
jest ostry oraz 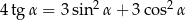 . Tangens kąta
. Tangens kąta  jest równy
jest równy
A)  B)
B) 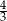 C)
C) 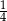 D) 4
D) 4
Jeżeli 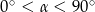 oraz
oraz 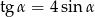 , to
, to
A) 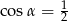 B)
B) 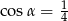 C)
C) 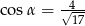 D)
D) 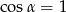
Jeżeli 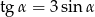 , oraz
, oraz  jest kątem ostrym, to
jest kątem ostrym, to
A) 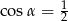 B)
B) 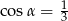 C)
C) 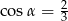 D)
D) 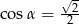
Jeżeli 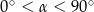 oraz
oraz 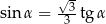 , to
, to
A) 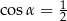 B)
B) 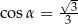 C)
C) 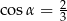 D)
D) 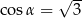
Kąt  jest ostry oraz
jest ostry oraz 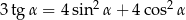 . Tangens kąta
. Tangens kąta  jest równy
jest równy
A)  B)
B) 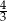 C)
C) 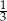 D) 3
D) 3
Liczba 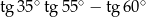 jest równa
jest równa
A) 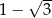 B)
B) 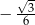 C)
C) 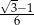 D)
D) 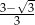
Wyrażenie 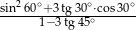 ma wartość
ma wartość
A)  B)
B) 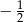 C)
C) 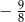 D)
D) 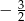
Wyrażenie 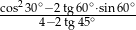 ma wartość
ma wartość
A) 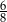 B)
B) 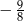 C)
C) 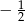 D)
D) 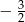
Wartość liczbowa wyrażenia 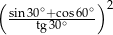 wynosi
wynosi
A) 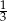 B)
B) 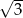 C) 3 D)
C) 3 D) 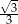
Wartość wyrażenia 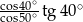 wynosi
wynosi
A) 1 B) 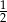 C)
C) 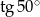 D)
D) 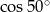
Wartość wyrażenia 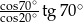 wynosi
wynosi
A) 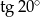 B)
B) 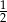 C) 1 D)
C) 1 D) 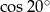
Wartość wyrażenia 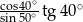 wynosi
wynosi
A) 1 B) 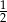 C)
C) 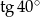 D)
D) 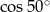
Wartość wyrażenia 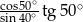 wynosi
wynosi
A) 1 B) 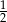 C)
C) 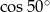 D)
D)