Ostrosłup ma tyle samo krawędzi bocznych, ile przekątnych ma jego podstawa. Liczba wszystkich wierzchołków tego ostrosłupa jest równa
A) 5 B) 6 C) 12 D) 10
/Szkoła średnia/Zadania testowe/Geometria/Stereometria
Ostrosłup i graniastosłup mają równe pola podstaw i równe wysokości. Objętość ostrosłupa jest równa 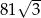 . Objętość graniastosłupa jest równa
. Objętość graniastosłupa jest równa
A) 27 B) 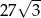 C) 243 D)
C) 243 D) 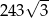
Ostrosłup i graniastosłup mają równe pola podstaw i równe wysokości. Objętość ostrosłupa jest równa 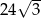 . Objętość graniastosłupa jest równa
. Objętość graniastosłupa jest równa
A) 8 B) 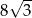 C)
C) 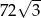 D) 72
D) 72
Suma długości wszystkich krawędzi i wszystkich przekątnych ścian sześcianu jest równa 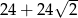 . Jaka jest objętość tego sześcianu?
. Jaka jest objętość tego sześcianu?
A) 8 B) 27 C) 64 D) 96
Suma długości wszystkich krawędzi sześcianu jest o 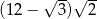 większa od długości przekątnej tego sześcianu. Pole powierzchni tego sześcianu jest równe
większa od długości przekątnej tego sześcianu. Pole powierzchni tego sześcianu jest równe
A) 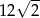 B) 12 C) 2 D)
B) 12 C) 2 D) 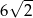
Jeżeli dodamy do siebie liczby wierzchołków, krawędzi i ścian ostrosłupa to otrzymamy 58. Ile krawędzi ma ten ostrosłup?
A) 29 B) 14 C) 28 D) 15
Jeżeli dodamy do siebie liczby wierzchołków, krawędzi i ścian ostrosłupa to otrzymamy 54. Ile krawędzi ma ten ostrosłup?
A) 26 B) 13 C) 28 D) 14
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Pole powierzchni całkowitej tego graniastosłupa jest równe 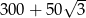 . Długość krawędzi tego graniastosłupa jest równa
. Długość krawędzi tego graniastosłupa jest równa
A) 12 B) 10 C) 9 D) 6
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Pole powierzchni całkowitej tego graniastosłupa jest równe 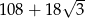 . Długość krawędzi tego graniastosłupa jest równa
. Długość krawędzi tego graniastosłupa jest równa
A) 12 B) 10 C) 9 D) 6
Dany jest ostrosłup prawidłowy trójkątny 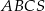 o podstawie
o podstawie 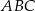 . Punkty
. Punkty 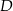 ,
, 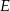 i
i 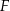 są środkami – odpowiednio – krawędzi bocznych
są środkami – odpowiednio – krawędzi bocznych 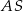 ,
, 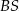 i
i 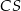 (zobacz rysunek).
(zobacz rysunek).
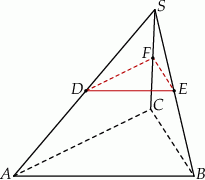
Stosunek objętości ostrosłupa 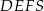 do objętości ostrosłupa
do objętości ostrosłupa 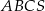 jest równy
jest równy
A) 3 : 4 B) 1 : 4 C) 1 : 8 D) 3 : 8
Dany jest ostrosłup prawidłowy trójkątny 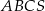 o podstawie
o podstawie 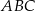 . Punkty
. Punkty 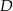 ,
, 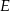 i
i 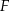 są punktami – odpowiednio – krawędzi bocznych
są punktami – odpowiednio – krawędzi bocznych 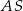 ,
, 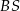 i
i 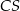 takimi, że
takimi, że 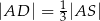 ,
, 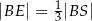 i
i 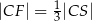 (zobacz rysunek).
(zobacz rysunek).
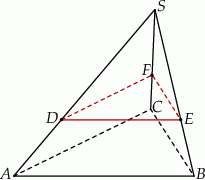
Stosunek objętości ostrosłupa 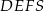 do objętości ostrosłupa
do objętości ostrosłupa 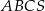 jest równy
jest równy
A) 8 : 27 B) 2 : 3 C) 8 : 9 D) 4 : 9
Z prostopadłościanu 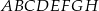 odcięto ostrosłup
odcięto ostrosłup 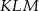 w ten sposób, że punkty
w ten sposób, że punkty 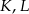 i
i 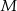 są środkami krawędzi
są środkami krawędzi 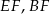 i
i 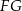 (zobacz rysunek).
(zobacz rysunek).
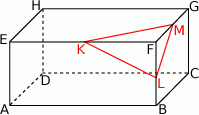
Ile razy objętość odciętego ostrosłupa jest mniejsza od objętości pozostałej części prostopadłościanu?
A) 48 razy. B) 47 razy. C) 46 razy. D) 24 razy.
Z koła o promieniu 12 wycięto dwa wycinki odpowiadające kątom środkowym 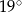 i
i 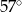 .
.
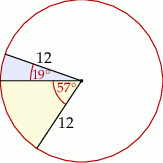
Następnie sklejono dwa stożki, których powierzchnie boczne utworzone zostały z otrzymanych wycinków. Ile razy pole podstawy większego z otrzymanych stożków jest większe od pola podstawy mniejszego stożka?
A) 3 B) 6 C) 9 D) 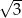
Na rysunkach poniżej przedstawiono siatki dwóch ostrosłupów.
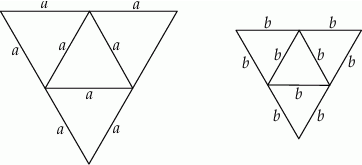
Pole powierzchni całkowitej ostrosłupa o krawędzi  jest dwa razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi
jest dwa razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi 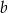 . Ile razy objętość ostrosłupa o krawędzi
. Ile razy objętość ostrosłupa o krawędzi  jest większa od objętości ostrosłupa o krawędzi
jest większa od objętości ostrosłupa o krawędzi 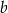 ?
?
A) 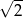 B) 2 C)
B) 2 C) 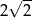 D) 4
D) 4
Na rysunkach poniżej przedstawiono siatki dwóch ostrosłupów.
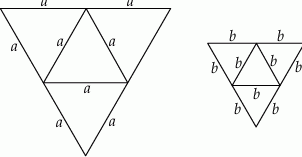
Pole powierzchni całkowitej ostrosłupa o krawędzi  jest trzy razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi
jest trzy razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi 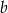 . Ile razy objętość ostrosłupa o krawędzi
. Ile razy objętość ostrosłupa o krawędzi  jest większa od objętości ostrosłupa o krawędzi
jest większa od objętości ostrosłupa o krawędzi 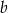 ?
?
A) 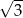 B)
B) 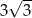 C) 3 D) 9
C) 3 D) 9
Krawędź sześcianu ma długość 9. Długość przekątnej tego sześcianu jest równa:
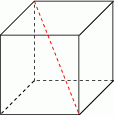
A) 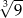 B)
B) 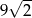 C)
C) 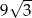 D)
D) 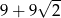
Krawędź sześcianu ma długość 6. Długość przekątnej tego sześcianu jest równa:
A) 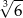 B)
B) 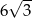 C)
C) 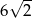 D)
D) 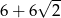
Przekątna ściany sześcianu ma długość 8. Przekątna tego sześcianu ma długość
A) 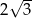 B)
B) 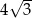 C)
C) 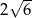 D)
D) 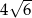
Przekątna ściany sześcianu ma długość 6. Przekątna tego sześcianu ma długość
A) 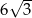 B)
B) 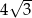 C)
C) 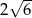 D)
D) 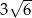
Przekątna ściany sześcianu ma długość 10. Przekątna tego sześcianu ma długość
A) 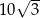 B)
B) 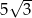 C)
C) 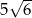 D)
D) 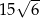
Przekątna ściany sześcianu ma długość 12. Przekątna tego sześcianu ma długość
A) 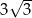 B)
B) 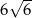 C)
C) 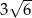 D)
D) 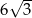
Powierzchnia boczna stożka po rozwinięciu jest półkolem o promieniu 12 cm. Podstawa tego stożka jest kołem o promieniu
A) 12 cm B) 6 cm C) 3 cm D) 1 cm
Po rozwinięciu powierzchni bocznej stożka na płaszczyźnie otrzymano połowę koła o promieniu 6. Promień podstawy tego stożka ma długość
A) 6 B)  C) 3 D)
C) 3 D) 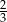
Po rozwinięciu powierzchni bocznej stożka na płaszczyźnie otrzymano jedną czwarta koła o promieniu 6. Promień podstawy tego stożka ma długość
A)  B)
B)  C) 3 D)
C) 3 D) 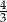
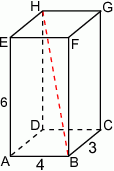
Wymiary prostopadłościanu 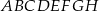 podane są na rysunku. Przekątna
podane są na rysunku. Przekątna 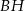 prostopadłościanu jest nachylona do płaszczyzny podstawy
prostopadłościanu jest nachylona do płaszczyzny podstawy 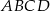 pod kątem
pod kątem  takim, że
takim, że
A) 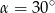 B)
B) 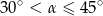 C)
C) 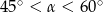 D)
D) 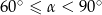
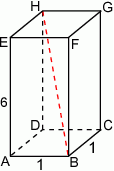
Wymiary prostopadłościanu 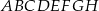 podane są na rysunku. Przekątna
podane są na rysunku. Przekątna 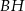 prostopadłościanu jest nachylona do płaszczyzny podstawy
prostopadłościanu jest nachylona do płaszczyzny podstawy 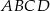 pod kątem
pod kątem  takim, że
takim, że
A) 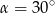 B)
B) 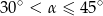 C)
C) 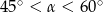 D)
D) 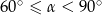
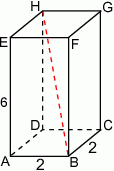
Wymiary prostopadłościanu 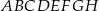 podane są na rysunku. Przekątna
podane są na rysunku. Przekątna 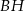 prostopadłościanu jest nachylona do płaszczyzny podstawy
prostopadłościanu jest nachylona do płaszczyzny podstawy 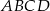 pod kątem
pod kątem  takim, że
takim, że
A) 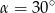 B)
B) 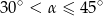 C)
C) 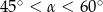 D)
D) 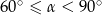
Objętość sześcianu jest równa 64. Przekątna ściany bocznej tego sześcianu ma długość
A) 4 B) 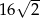 C)
C) 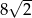 D)
D) 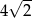
Objętość sześcianu jest równa 27. Przekątna ściany bocznej tego sześcianu ma długość
A) 3 B) 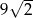 C)
C) 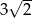 D)
D) 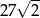
Objętość sześcianu jest równa 125. Przekątna ściany bocznej tego sześcianu ma długość
A) 5 B) 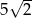 C)
C) 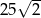 D)
D) 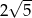
Dany jest ostrosłup prawidłowy czworokątny o krawędzi podstawy długości 80 cm i krawędzi bocznej długości 90 cm (zobacz rysunek), a ponadto dane są cztery odcinki 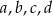 , o długościach – odpowiednio – 53 cm, 59 cm, 63 cm i 69 cm.
, o długościach – odpowiednio – 53 cm, 59 cm, 63 cm i 69 cm.
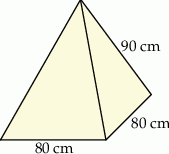
Wysokość tego ostrosłupa jest dłuższa
A) tylko od odcinka  .
.
B) tylko od odcinków  i
i 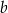 .
.
C) tylko od odcinków 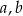 i
i  .
.
D) od wszystkich czterech danych odcinków.
Dany jest graniastosłup prawidłowy sześciokątny 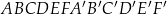 , w którym krawędź podstawy ma długość 5. Przekątna
, w którym krawędź podstawy ma długość 5. Przekątna 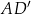 tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 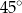 (zobacz rysunek).
(zobacz rysunek).
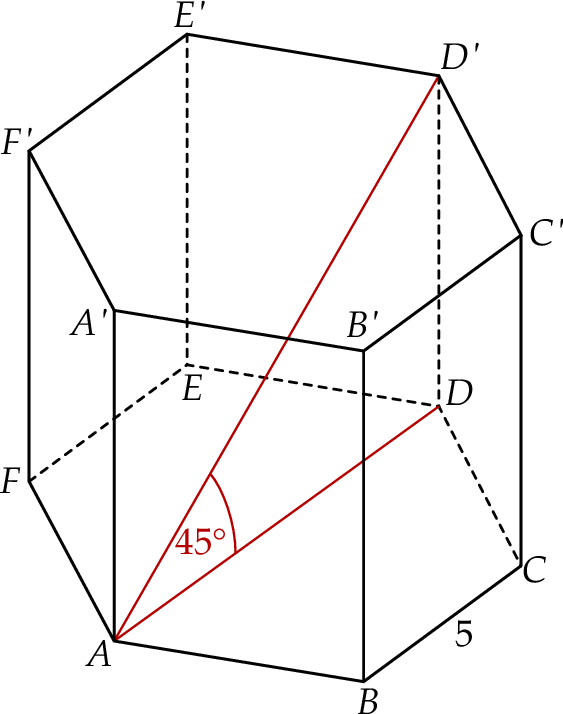
Pole ściany bocznej tego graniastosłupa jest równe
A) 12,5 B) 25 C) 50 D) 100
Dany jest graniastosłup prawidłowy sześciokątny 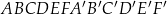 , w którym krawędź podstawy ma długość 3. Przekątna
, w którym krawędź podstawy ma długość 3. Przekątna 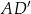 tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 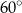 (zobacz rysunek).
(zobacz rysunek).
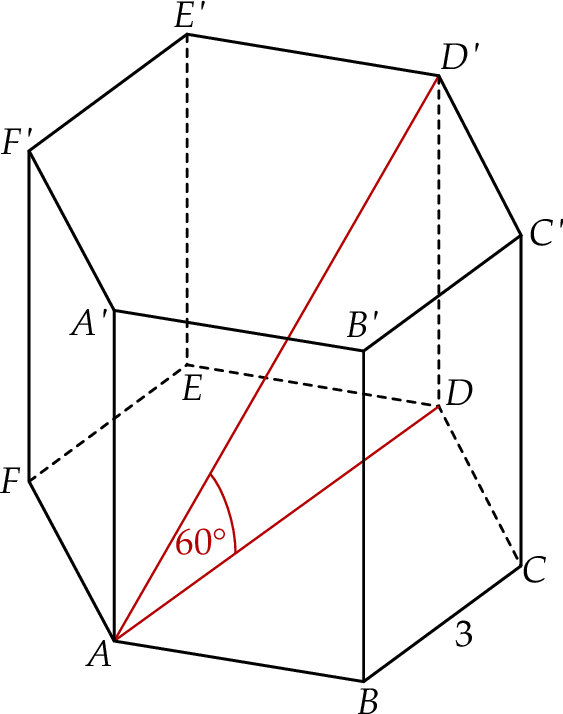
Pole ściany bocznej tego graniastosłupa jest równe
A) 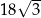 B)
B) 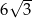 C)
C) 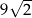 D) 90
D) 90
Przekątna graniastosłupa prawidłowego czworokątnego ma długość 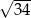 , a krawędź podstawy ma długość 3. Objętość tego graniastosłupa jest równa
, a krawędź podstawy ma długość 3. Objętość tego graniastosłupa jest równa
A) 4 B) 18 C) 36 D) 24
Ceramiczna ozdoba ma kształt czworościanu foremnego o krawędzi długości 6 dm (zobacz rysunek).
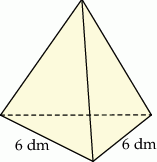
Wysokość tego czworościanu jest – z dokładnością do 0,01 dm – równa
A) 3,46 dm B) 4,9 dm C) 5,2 dm D) 4,8 dm
W graniastosłupie prawidłowym stosunek liczby wszystkich krawędzi do liczby wszystkich ścian jest równy 7 : 3. Podstawą tego graniastosłupa jest
A) trójkąt. B) pięciokąt. C) siedmiokąt. D) ośmiokąt.
W ostrosłupie prawidłowym czworokątnym 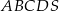 wszystkie krawędzie mają jednakową długość.
wszystkie krawędzie mają jednakową długość.
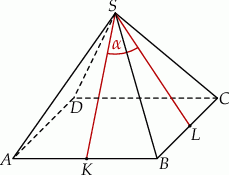
Oblicz cosinus kąta utworzonego przez wysokości 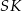 i
i 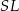 dwóch sąsiednich ścian bocznych.
dwóch sąsiednich ścian bocznych.

