Promień podstawy walca zwiększamy trzy razy, a jego wysokość zmniejszamy trzy razy. Wówczas objętość walca
A) zwiększy się trzy razy B) zmniejszy się trzy razy
C) zwiększy się o trzy D) nie zmieni się
/Szkoła średnia/Zadania testowe/Geometria/Stereometria
Promień podstawy walca zmniejszamy trzy razy, a jego wysokość zwiększamy trzy razy. Wówczas objętość walca
A) zwiększy się trzy razy B) zmniejszy się trzy razy
C) zwiększy się o trzy D) nie zmieni się
Promień podstawy walca zwiększamy cztery razy, a jego wysokość zmniejszamy cztery razy. Wówczas objętość walca
A) nie zmieni się B) zwiększy się o cztery
C) zmniejszy się cztery razy D) zwiększy się cztery razy
Podstawą ostrosłupa jest kwadrat 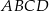 o boku długości 1. Wysokością tego ostrosłupa jest krawędź
o boku długości 1. Wysokością tego ostrosłupa jest krawędź 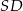 , a długość krawędzi
, a długość krawędzi 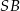 jest równa 2 (zobacz rysunek).
jest równa 2 (zobacz rysunek).
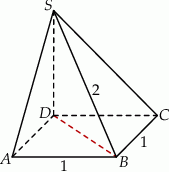
Różnica miar kątów 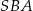 i
i 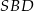 jest równa
jest równa
A) 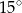 B)
B) 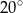 C)
C) 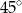 D)
D) 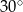
Objętość walca wynosi 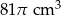 . Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
. Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
A) 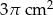 B)
B) 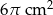 C)
C) 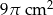 D)
D) 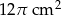
Objętość sześcianu jest równa 64. Pole powierzchni całkowitej tego sześcianu jest równe
A) 512 B) 384 C) 96 D) 16
Rysunek przedstawia siatkę ostrosłupa prostego o podstawie będącej prostokątem.
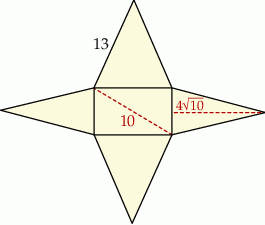
Objętość tego ostrosłupa jest równa
A) 192 B) 96 C) 576 D) 384
Dany jest trójkąt prostokątny o długościach boków 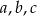 , gdzie
, gdzie 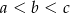 . Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt 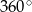 , otrzymujemy bryłę, której pole powierzchni całkowitej jest równe
, otrzymujemy bryłę, której pole powierzchni całkowitej jest równe
A) 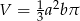 B)
B) 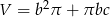 C)
C) 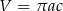 D)
D) 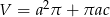
Jeśli promień podstawy stożka zwiększymy trzykrotnie, a wysokość zmniejszymy trzykrotnie, to objętość stożka
A) zwiększy się dziewięciokrotnie B) nie zmieni się
C) zwiększy się trzykrotnie D) zwiększy się sześciokrotnie
Jeśli promień podstawy stożka zmniejszymy trzykrotnie, a wysokość zwiększymy trzykrotnie, to objętość stożka
A) zwiększy się dziewięciokrotnie B) nie zmieni się
C) zwiększy się trzykrotnie D) zmniejszy się trzykrotnie
Jeśli promień podstawy stożka zwiększymy dwukrotnie, a wysokość zmniejszymy dwukrotnie, to objętość stożka
A) zwiększy się dwukrotnie B) nie zmieni się
C) zwiększy się czterokrotnie D) zmniejszy się czterokrotnie
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt  , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy 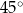 (zobacz rysunek).
(zobacz rysunek).
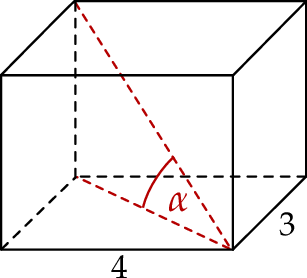
Wysokość graniastosłupa jest równa
A) 5 B) 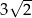 C)
C) 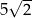 D)
D) 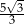
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt  , jaki tworzą dwie przekątne tego graniastosłupa, jest równy
, jaki tworzą dwie przekątne tego graniastosłupa, jest równy 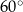 (zobacz rysunek).
(zobacz rysunek).
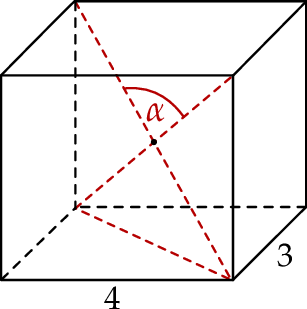
Wysokość graniastosłupa jest równa
A) 10 B) 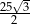 C)
C) 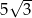 D)
D) 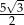
Graniastosłup prosty ma pole powierzchni całkowitej równe 94, a w jego podstawie jest prostokąt o bokach długości 3 i 4 (zobacz rysunek).
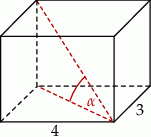
Kąt  , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
A) 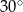 B)
B) 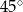 C)
C) 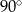 D)
D) 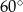
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt  , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy 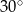 (zobacz rysunek).
(zobacz rysunek).
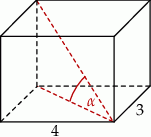
Wysokość graniastosłupa jest równa
A) 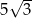 B)
B) 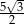 C)
C) 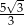 D)
D) 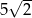
Objętość kuli o promieniu 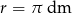 jest równa
jest równa
A) 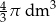 B)
B) 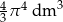 C)
C) 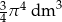 D)
D) 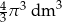
Objętość kuli o promieniu 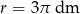 jest równa
jest równa
A) 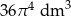 B)
B) 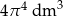 C)
C) 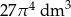 D)
D) 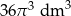
Przekątna przekroju osiowego walca jest o 13 dłuższa od promienia podstawy tego walca, oraz o 2 dłuższa od jego wysokości. Pole podstawy tego walca jest równe
A) 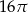 B)
B) 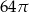 C)
C) 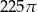 D)
D) 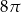
Promień 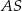 podstawy walca jest równy wysokości
podstawy walca jest równy wysokości 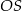 tego walca. Sinus kąta
tego walca. Sinus kąta 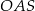 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
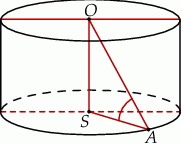
A) 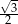 B)
B) 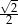 C)
C) 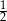 D) 1
D) 1
Promień 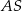 podstawy walca jest równy wysokości
podstawy walca jest równy wysokości 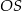 tego walca. Tangens kąta
tego walca. Tangens kąta 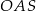 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
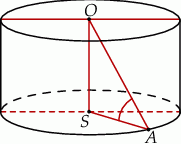
A) 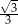 B)
B) 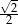 C)
C) 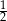 D) 1
D) 1
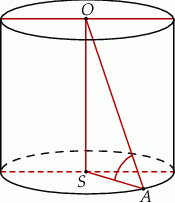
Promień 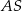 podstawy walca jest równy połowie wysokości
podstawy walca jest równy połowie wysokości 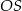 tego walca. Sinus kąta
tego walca. Sinus kąta 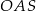 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
A) 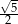 B)
B) 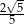 C)
C) 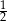 D) 1
D) 1
Przekątna graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 2 razy dłuższa od krawędzi podstawy, jest równa 6. Wynika stąd, że objętość tego graniastosłupa jest równa
A) 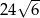 B)
B) 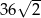 C)
C) 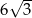 D)
D) 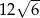
Przekrój osiowy stożka jest trójkątem równoramiennym o ramieniu długości 12. Kąt rozwarcia stożka ma miarę 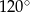 . Objętość stożka wynosi
. Objętość stożka wynosi
A) 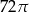 B)
B) 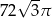 C)
C) 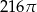 D)
D) 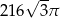
Powierzchnia sześcianu wynosi 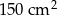 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 4 cm B) 5 cm C) 5,5 cm D) 6 cm
Powierzchnia sześcianu wynosi 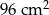 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 4 cm B) 5 cm C) 5,5 cm D) 6 cm
Pole powierzchni całkowitej sześcianu jest równe 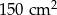 . Długość krawędzi tego sześcianu jest równa
. Długość krawędzi tego sześcianu jest równa
A) 3,5 cm B) 4 cm C) 4,5 cm D) 5 cm
Powierzchnia sześcianu wynosi 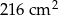 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 3 cm B) 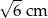 C) 12 cm D) 6 cm
C) 12 cm D) 6 cm
Objętość sześcianu jest równa 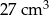 . Jaka jest suma długości wszystkich krawędzi tego sześcianu?
. Jaka jest suma długości wszystkich krawędzi tego sześcianu?
A) 18 cm B) 36 cm C) 24 cm D) 12 cm
Objętość sześcianu jest równa 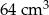 . Jaka jest suma długości wszystkich krawędzi tego sześcianu?
. Jaka jest suma długości wszystkich krawędzi tego sześcianu?
A) 48 cm B) 36 cm C) 24 cm D) 64 cm
Dane są graniastosłup i ostrosłup o takich samych podstawach. Liczba wszystkich wierzchołków tego graniastosłupa jest o 9 większa od liczby wszystkich wierzchołków tego ostrosłupa. Podstawą każdej z tych brył jest
A) dziewięciokąt. B) ośmiokąt. C) osiemnastokąt. D) dziesięciokąt.
Dane są graniastosłup i ostrosłup o takich samych podstawach. Liczba wszystkich wierzchołków tego graniastosłupa jest o 10 większa od liczby wszystkich wierzchołków tego ostrosłupa. Podstawą każdej z tych brył jest
A) dziewięciokąt. B) ośmiokąt. C) jedenastokąt. D) dziesięciokąt.
Przekątna graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości tego graniastosłupa. Z tego wynika, że miara kąta, jaki tworzy ta przekątna z podstawą, jest równa
A) 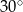 B)
B) 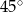 C)
C) 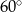 D)
D) 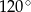
Przekątna graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od przekątnej podstawy tego graniastosłupa. Z tego wynika, że miara kąta, jaki tworzy ta przekątna z podstawą, jest równa
A) 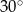 B)
B) 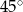 C)
C) 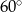 D)
D) 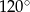
Długość przekątnej podstawy graniastosłupa prawidłowego czworokątnego jest równa długości jego wysokości. Z tego wynika, że miara kąta, jaki tworzy przekątna graniastosłupa z podstawą, jest równa
A) 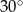 B)
B) 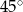 C)
C) 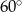 D)
D) 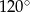
Pole powierzchni bocznej walca wynosi 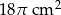 . Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
. Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
A) 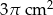 B)
B) 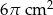 C)
C) 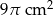 D)
D)