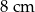Liczba krawędzi graniastosłupa jest o 10 większa od liczby jego ścian. Ile wierzchołków ma ten graniastosłup?
A) 6 B) 18 C) 24 D) 12
/Szkoła średnia/Zadania testowe/Geometria/Stereometria
Liczba wszystkich krawędzi graniastosłupa jest o 10 większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest
A) czworokąt B) pięciokąt C) sześciokąt D) dziesięciokąt
Liczba krawędzi graniastosłupa jest o 8 większa od liczby jego ścian. Ile wierzchołków ma ten graniastosłup?
A) 5 B) 15 C) 10 D) 16
Liczba wszystkich krawędzi graniastosłupa jest o 12 większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest
A) czworokąt B) pięciokąt C) sześciokąt D) dziesięciokąt
Kąt rozwarcia stożka ma miarę 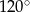 , a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy
, a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy
A) 3 B) 6 C) 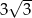 D)
D) 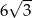
Kąt rozwarcia stożka ma miarę 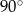 , a tworząca tego stożka ma długość 8. Promień podstawy stożka jest równy
, a tworząca tego stożka ma długość 8. Promień podstawy stożka jest równy
A) 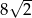 B) 4 C)
B) 4 C) 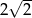 D)
D) 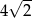
Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy
A) 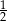 B)
B) 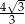 C) 1 D)
C) 1 D) 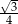
Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego jest 3 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy
A) 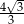 B)
B) 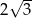 C)
C) 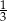 D)
D) 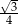
Pięć identycznych metalowych stożków o promieniu podstawy  przetopiono na jeden walec, którego wysokość jest równa
przetopiono na jeden walec, którego wysokość jest równa 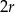 i jest dwa razy krótsza od jego promienia podstawy. Gdyby te same stożki przetopiono na kule o promieniu
i jest dwa razy krótsza od jego promienia podstawy. Gdyby te same stożki przetopiono na kule o promieniu  , to ile takich kul by otrzymano?
, to ile takich kul by otrzymano?
A) 32 B) 16 C) 8 D) 24
Wysokość 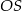 walca jest równa 2, a cosinus kąta
walca jest równa 2, a cosinus kąta 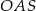 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy  .
.
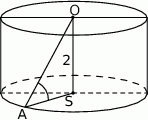
Pole powierzchni bocznej tego walca jest równe
A) 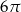 B)
B) 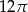 C)
C) 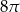 D)
D) 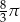
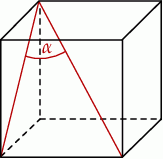
Jeżeli  oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
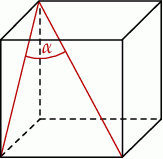
A) 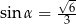 B)
B) 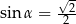 C)
C) 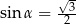 D)
D) 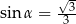
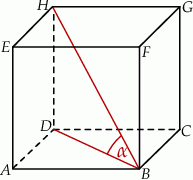
Dany jest sześcian 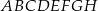 . Sinus kąta
. Sinus kąta  nachylenia przekątnej
nachylenia przekątnej 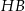 tego sześcianu do płaszczyzny podstawy
tego sześcianu do płaszczyzny podstawy 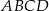 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
A) 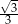 B)
B) 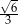 C)
C) 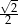 D)
D) 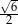
Jeżeli  oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
A) 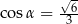 B)
B) 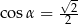 C)
C) 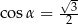 D)
D) 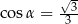
Jeżeli  oznacza miarę kąta między przekątnymi ścian sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątnymi ścian sześcianu (zobacz rysunek), to
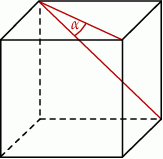
A) 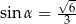 B)
B) 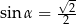 C)
C) 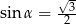 D)
D) 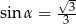
Zbiór punktów wspólnych kuli i prostej może być
A) zbiorem dwuelementowym B) zbiorem jednoelementowym C) okręgiem D) kołem
Zbiór punktów wspólnych kuli i płaszczyzny może być
A) zbiorem dwuelementowym B) okręgiem C) zbiorem jednoelementowym D) sferą
Ostrosłup ma 12 krawędzi. Liczba wszystkich wierzchołków tego ostrosłupa jest równa
A) 12 B) 9 C) 8 D) 7
Jeśli ostrosłup ma 50 krawędzi, to liczba jego ścian jest równa
A) 50 B) 26 C) 25 D) 22
Ostrosłup, który ma 12 krawędzi, ma
A) 6 ścian B) 7 ścian C) 8 ścian D) 9 ścian
Jeżeli ostrosłup ma 10 krawędzi, to liczba ścian bocznych jest równa
A) 5 B) 7 C) 8 D) 10
Dany jest sześcian 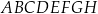 o krawędzi długości 5. Wewnątrz sześcianu znajduje się punkt
o krawędzi długości 5. Wewnątrz sześcianu znajduje się punkt  (zobacz rysunek).
(zobacz rysunek).
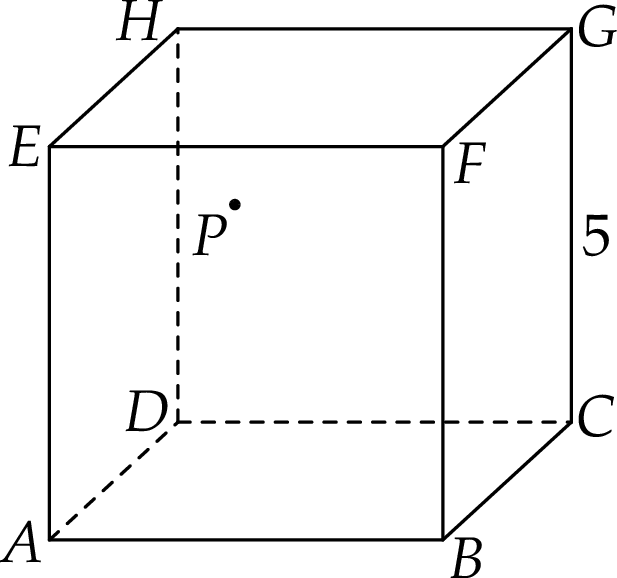
Suma odległości punktu 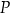 od wszystkich ścian sześcianu
od wszystkich ścian sześcianu 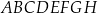 jest równa
jest równa
A) 15 B) 20 C) 25 D) 30
Powierzchnia boczna walca o objętości 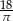 po rozwinięciu jest prostokątem, w którym przekątna tworzy z wysokością walca kąt o mierze
po rozwinięciu jest prostokątem, w którym przekątna tworzy z wysokością walca kąt o mierze 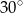 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 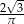 B)
B) 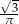 C)
C) 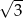 D)
D) 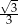
Krawędź podstawy ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od jego wysokości. Kąt nachylenia ściany bocznej do podstawy ma miarę
A) 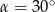 B)
B) 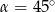 C)
C) 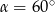 D)
D) 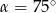
Dany jest prostopadłościan 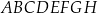 , w którym podstawy
, w którym podstawy 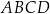 i
i 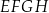 są kwadratami o boku długości 6. Przekątna
są kwadratami o boku długości 6. Przekątna 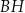 tego prostopadłościanu tworzy z przekątną
tego prostopadłościanu tworzy z przekątną 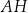 ściany bocznej
ściany bocznej 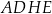 kąt o mierze
kąt o mierze 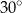 (zobacz rysunek).
(zobacz rysunek).
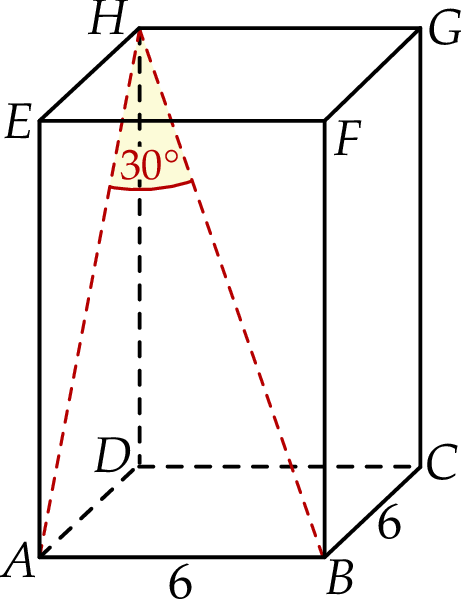
Przekątna 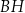 tego prostopadłościanu ma długość równą
tego prostopadłościanu ma długość równą
A) 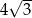 B)
B) 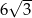 C) 12 D)
C) 12 D) 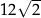
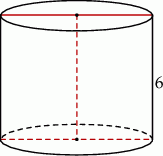
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
A) 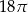 B)
B) 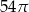 C)
C) 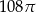 D)
D) 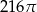
Przekrój osiowy walca jest kwadratem o boku 10. Objętość tego walca jest równa
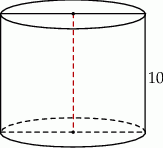
A) 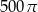 B)
B) 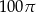 C)
C) 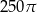 D)
D) 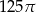
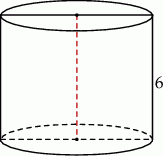
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
A) 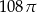 B)
B) 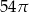 C)
C) 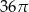 D)
D) 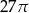
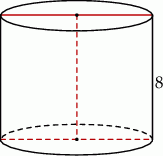
Przekrój osiowy walca jest kwadratem o boku długości 8. Objętość tego walca jest równa
A) 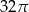 B)
B) 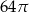 C)
C) 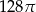 D)
D) 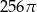
Jeżeli przekrój osiowy walca jest kwadratem o boku 4, to objętość walca jest równa
A) 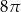 B)
B) 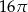 C)
C) 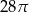 D)
D) 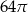
Stosunek pól powierzchni dwóch kul jest równy 1:9. Wobec tego stosunek objętości tych kul jest równy
A) 1:3 B) 1:9 C) 1:27 D) 1:81
Stosunek pól powierzchni dwóch kul jest równy 1:16. Wobec tego stosunek objętości tych kul jest równy
A) 1:256 B) 1:64 C) 1:16 D) 1:4
Stosunek pól powierzchni dwóch kul jest równy 1:4. Wobec tego stosunek objętości tych kul jest równy
A) 1:2 B) 1:8 C) 1:4 D) 1:16
Jeśli promień kuli zwiększymy o 30%, to pole powierzchni kuli wzrośnie o:
A) 30% B) 60% C) 69% D) ponad 100%
Jeśli promień kuli zmniejszymy o 50%, to pole powierzchni kuli zmaleje o:
A) 30% B) 60% C) 75% D) ponad 90%
Jeśli promień kuli zwiększymy o 50%, to pole powierzchni kuli wzrośnie o:
A) 30% B) 60% C) 69% D) ponad 100%
Dany jest prostopadłościan 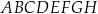 , w którym prostokąty
, w którym prostokąty 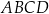 i
i 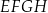 są jego podstawami. Odcinek
są jego podstawami. Odcinek 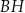 jest przekątną tego prostopadłościanu. Na którym rysunku prawidłowo oznaczono i podpisano kąt
jest przekątną tego prostopadłościanu. Na którym rysunku prawidłowo oznaczono i podpisano kąt  pomiędzy przekątną
pomiędzy przekątną 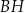 prostopadłościanu a jego ścianą boczną
prostopadłościanu a jego ścianą boczną 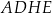 ?
?
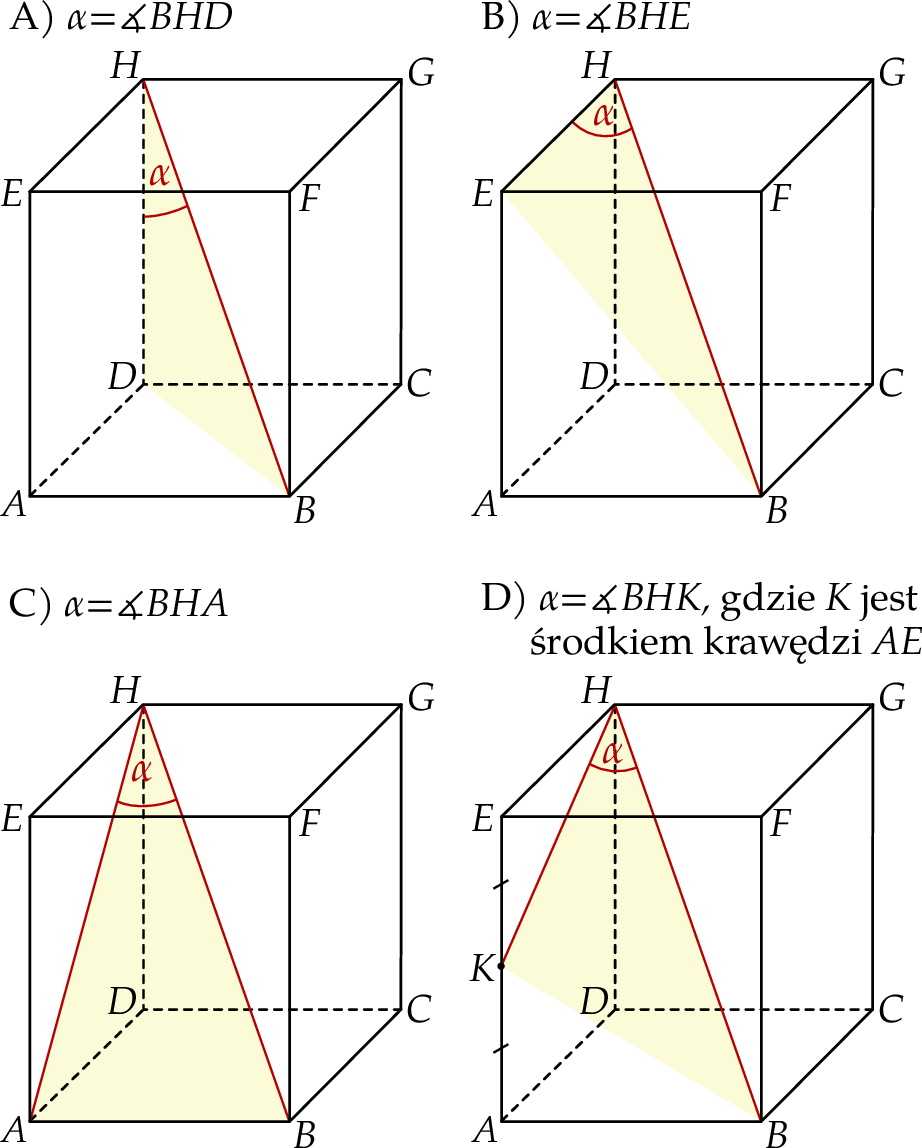
Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 15. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod  takim, że
takim, że 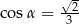 . Długość przekątnej tego graniastosłupa jest równa
. Długość przekątnej tego graniastosłupa jest równa
A) 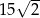 B) 45 C)
B) 45 C) 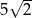 D) 10
D) 10
Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 12. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod  takim, że
takim, że 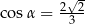 . Długość przekątnej tego graniastosłupa jest równa
. Długość przekątnej tego graniastosłupa jest równa
A) 18 B) 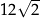 C)
C) 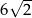 D) 8
D) 8
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają jednakową długość, a pole powierzchni całkowitej tego ostrosłupa jest równe 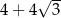 . Wobec tego długość wysokości tego ostrosłupa jest równa
. Wobec tego długość wysokości tego ostrosłupa jest równa
A) 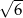 B) 2 C)
B) 2 C) 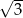 D)
D) 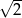
Pole podstawy stożka jest trzy razy mniejsze od jego pola powierzchni bocznej. Wówczas kąt  rozwarcia stożka spełnia warunek
rozwarcia stożka spełnia warunek
A) 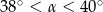 B)
B) 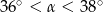 C)
C) 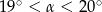 D)
D) 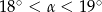
Pole powierzchni całkowitej sześcianu jest równe 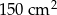 . Długość przekątnej podstawy tego sześcianu jest równa
. Długość przekątnej podstawy tego sześcianu jest równa
A) 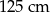 B)
B) 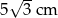 C)
C) 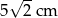 D)
D) 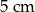
Pole powierzchni całkowitej sześcianu jest równe 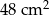 . Długość przekątnej podstawy tego sześcianu jest równa
. Długość przekątnej podstawy tego sześcianu jest równa
A) 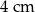 B)
B) 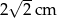 C)
C) 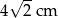 D)
D)