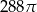Przekątna prostopadłościanu o wymiarach 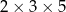 ma długość
ma długość
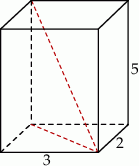
A) 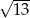 B)
B) 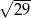 C)
C) 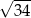 D)
D) 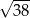
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Przekątna prostopadłościanu o wymiarach 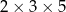 ma długość
ma długość

A) 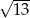 B)
B) 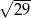 C)
C) 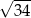 D)
D) 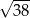
Przekątna prostopadłościanu o wymiarach 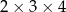 ma długość
ma długość
A) 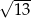 B)
B) 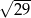 C) 5 D) 6
C) 5 D) 6
Przekątna prostopadłościanu o wymiarach 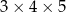 ma długość
ma długość
A) 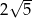 B)
B) 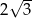 C)
C) 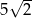 D)
D) 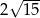
Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość 4 cm, a wysokość jego ściany bocznej ma długość 5 cm. Pole powierzchni bocznej tego ostrosłupa jest równe
A) 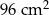 B)
B) 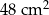 C)
C) 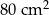 D)
D) 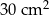
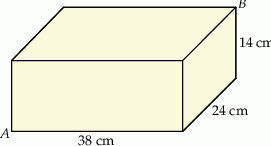
Pudełko w kształcie prostopadłościanu ma wymiary 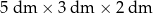 (zobacz rysunek).
(zobacz rysunek).
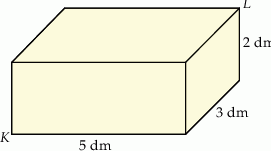
Przekątna 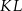 tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
A) 5,83 dm B) 6,16 dm C) 3,61 dm D) 5,39 dm
Bloczek betonowy fundamentowy ma kształt prostopadłościanu o wymiarach 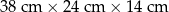 (zobacz rysunek).
(zobacz rysunek).
Przekątna 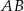 tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
A) 4,71 dm B) 4,49 dm C) 4,05 dm D) 4,7 dm
Pudełko w kształcie prostopadłościanu ma wymiary 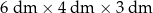 (zobacz rysunek).
(zobacz rysunek).
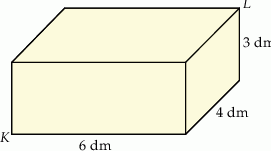
Przekątna 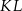 tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
A) 6,83 dm B) 6,16 dm C) 7,81 dm D) 5,39 dm
Podstawą ostrosłupa jest prostokąt 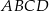 o bokach długości:
o bokach długości: 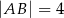 i
i 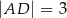 . Krawędź boczna
. Krawędź boczna 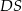 jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
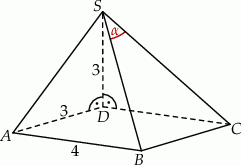
Jeżeli  jest katem pomiędzy krawędziami bocznymi
jest katem pomiędzy krawędziami bocznymi 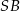 i
i 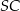 , to
, to
A) 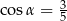 B)
B) 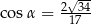 C)
C) 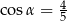 D)
D) 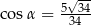
Podstawą ostrosłupa jest kwadrat 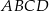 o boku długości 4. Krawędź boczna
o boku długości 4. Krawędź boczna 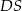 jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
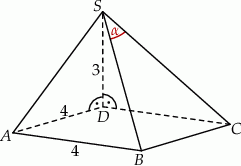
Jeżeli  jest katem pomiędzy krawędziami bocznymi
jest katem pomiędzy krawędziami bocznymi 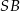 i
i 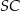 , to
, to
A) 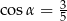 B)
B) 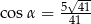 C)
C) 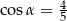 D)
D) 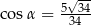
Objętość stożka o wysokości 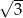 i kącie rozwarcia
i kącie rozwarcia  jest równa
jest równa
A) 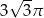 B)
B) 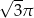 C)
C) 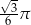 D)
D) 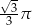
Kąt rozwarcia stożka ma miarę 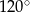 , a wysokość tego stożka ma długość 3. Objętość tego stożka jest równa
, a wysokość tego stożka ma długość 3. Objętość tego stożka jest równa
A) 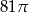 B)
B) 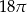 C)
C) 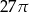 D)
D) 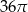
Kąt rozwarcia stożka ma miarę 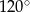 , a tworząca tego stożka ma długość 4. Objętość tego stożka jest równa
, a tworząca tego stożka ma długość 4. Objętość tego stożka jest równa
A) 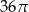 B)
B) 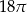 C)
C) 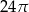 D)
D) 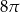
Krawędź podstawy graniastosłupa prawidłowego trójkątnego stanowi  wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
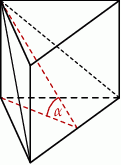
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt  o mierze
o mierze
A) 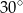 B)
B) 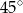 C)
C) 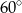 D)
D) 
Wysokość graniastosłupa prawidłowego trójkątnego jest równa połowie długości jego krawędzi podstawy. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
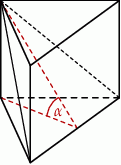
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt  o mierze
o mierze
A) 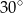 B)
B) 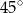 C)
C) 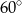 D)
D) 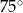
Podstawą ostrosłupa jest równoramienny trójkąt prostokątny 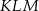 o przeciwprostokątnej długości
o przeciwprostokątnej długości 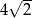 . Wysokością tego ostrosłupa jest krawędź
. Wysokością tego ostrosłupa jest krawędź 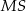 o długości 4 (zobacz rysunek).
o długości 4 (zobacz rysunek).
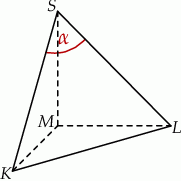
Kąt  , jaki tworzą krawędzie
, jaki tworzą krawędzie 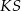 i
i 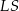 , spełnia warunek
, spełnia warunek
A) 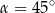 B)
B) 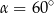 C)
C) 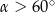 D)
D) 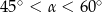
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 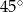 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 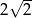 B)
B) 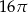 C)
C) 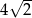 D)
D) 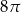
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 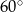 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 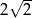 B)
B) 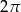 C)
C) 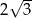 D) 2
D) 2
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 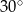 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 2 B) 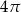 C)
C) 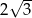 D)
D) 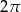
Powierzchnię boczną graniastosłupa prawidłowego czworokątnego o objętości 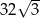 rozcięto wzdłuż krawędzi bocznej graniastosłupa i rozłożono na płaszczyźnie. Otrzymano w ten sposób prostokąt
rozcięto wzdłuż krawędzi bocznej graniastosłupa i rozłożono na płaszczyźnie. Otrzymano w ten sposób prostokąt 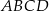 , w którym bok
, w którym bok 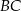 odpowiada krawędzi rozcięcia (wysokości graniastosłupa), a przekątna
odpowiada krawędzi rozcięcia (wysokości graniastosłupa), a przekątna 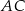 tworzy z bokiem
tworzy z bokiem 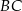 kąt o mierze
kąt o mierze 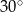 (zobacz rysunek).
(zobacz rysunek).
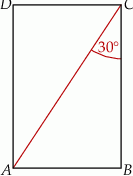
Długość krawędzi podstawy tego graniastosłupa jest równa.
A) 4 B) 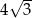 C)
C) 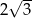 D) 2
D) 2
W każdym  –kącie wypukłym (
–kącie wypukłym (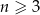 ) liczba przekątnych jest równa
) liczba przekątnych jest równa 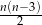 . Jeżeli graniastosłup prosty ma
. Jeżeli graniastosłup prosty ma 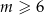 wierzchołków, to liczba wszystkich przekątnych jego podstaw i ścian bocznych jest równa
wierzchołków, to liczba wszystkich przekątnych jego podstaw i ścian bocznych jest równa
A) 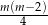 B)
B) 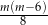 C)
C) 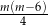 D)
D) 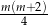
Przekrój osiowy walca jest prostokątem, w którym przekątne przecinają się pod kątem 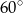 . Wysokość walca jest równa
. Wysokość walca jest równa 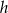 i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
A) 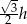 B)
B) 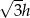 C)
C) 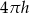 D)
D) 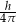
Przekrój osiowy walca jest prostokątem, w którym przekątne przecinają się pod kątem 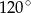 . Wysokość walca jest równa
. Wysokość walca jest równa 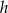 i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
A) 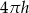 B)
B) 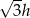 C)
C) 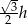 D)
D) 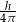
Pole powierzchni jednej ściany sześcianu jest równe 4. Objętość tego sześcianu jest równa
A) 6 B) 8 C) 24 D) 64
Pole powierzchni jednej ściany sześcianu jest równe 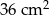 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa
A) 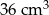 B)
B) 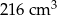 C)
C) 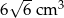 D)
D) 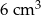
Pole powierzchni jednej ściany sześcianu jest równe 9. Objętość tego sześcianu jest równa
A) 9 B) 27 C) 54 D) 81
Suma długości wszystkich przekątnych sześcianu jest równa 24. Pole powierzchni całkowitej tego sześcianu jest równe
A) 144 B) 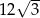 C) 36 D) 72
C) 36 D) 72
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 3 razy dłuższa od krawędzi podstawy, jest równe 140. Zatem krawędź podstawy tego graniastosłupa jest równa
A) 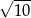 B)
B) 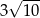 C)
C) 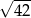 D)
D) 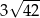
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 3 razy krótsza od krawędzi podstawy, jest równe 60. Zatem krawędź podstawy tego graniastosłupa jest równa
A) 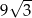 B)
B) 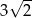 C)
C) 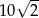 D)
D) 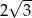
Promień kuli jest równy promieniowi podstawy walca, oraz objętości obu brył są równe. Stosunek pola powierzchni kuli do pola powierzchni całkowitej walca jest równy
A) 1 B)  C)
C) 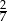 D)
D) 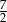
Dany jest stożek o objętości 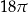 , którego przekrojem osiowym jest trójkąt
, którego przekrojem osiowym jest trójkąt 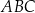 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 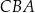 jest kątem nachylenia tworzącej
jest kątem nachylenia tworzącej 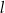 tego stożka do płaszczyzny jego podstawy. Tangens kąta
tego stożka do płaszczyzny jego podstawy. Tangens kąta 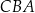 jest równy 2.
jest równy 2.
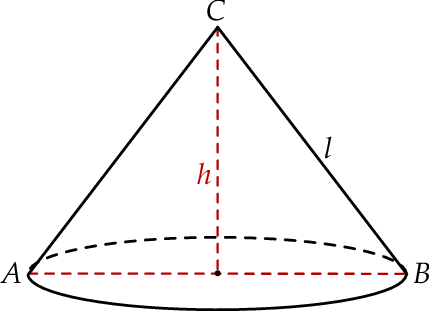
Wynika stąd, że wysokość 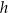 tego stożka jest równa
tego stożka jest równa
A) 12 B) 6 C) 4 D) 2
Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 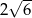 . Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze
. Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze 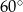 . Wysokość tego graniastosłupa ma długość
. Wysokość tego graniastosłupa ma długość
A) 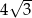 B) 6 C) 12 D) 4
B) 6 C) 12 D) 4
Przekątna graniastosłupa prawidłowego czworokątnego ma długość równą 16 i jest nachylona do płaszczyzny podstawy pod kątem 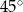 . Wysokość tego graniastosłupa ma długość równą
. Wysokość tego graniastosłupa ma długość równą
A) 8 B) 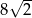 C)
C) 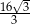 D)
D) 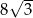
Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 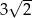 . Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze
. Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze 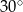 . Wysokość tego graniastosłupa ma długość
. Wysokość tego graniastosłupa ma długość
A) 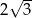 B) 6 C)
B) 6 C) 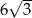 D) 4
D) 4
Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe 36, a miara kąta nachylenia przekątnej graniastosłupa do płaszczyzny jego podstawy jest równa 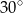 . Wysokość tego graniastosłupa jest równa
. Wysokość tego graniastosłupa jest równa
A) 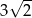 B)
B) 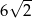 C)
C) 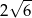 D)
D) 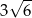
Przekątna graniastosłupa prawidłowego czworokątnego o długości równej 10 cm jest nachylona do płaszczyzny podstawy pod kątem 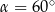 . Wysokość tego graniastosłupa ma długość równą
. Wysokość tego graniastosłupa ma długość równą
A) 5 cm B) 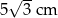 C)
C) 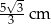 D)
D) 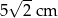
W graniastosłupie prawidłowym sześciokątnym 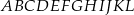 wierzchołki
wierzchołki 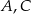 i
i 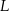 połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.
połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.
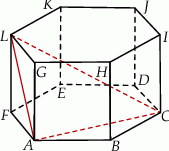
Cosinus największego kąta trójkąta 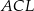 jest równy
jest równy
A)  B)
B) 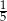 C) 0 D)
C) 0 D) 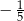
Przekrój osiowy stożka jest trójkątem równoramiennym o stosunku ramienia do podstawy 3:2. Tworząca stożka tworzy z podstawą kąt  , taki, że
, taki, że
A) 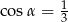 B)
B) 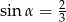 C)
C) 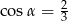 D)
D) 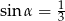
Przekrój osiowy stożka jest trójkątem równoramiennym o stosunku ramienia do podstawy 5:2. Tworząca stożka tworzy z podstawą kąt  , taki, że
, taki, że
A) 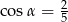 B)
B) 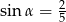 C)
C) 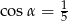 D)
D) 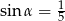
Przekrój osiowy stożka jest trójkątem równoramiennym o stosunku ramienia do podstawy 8:6. Tworząca stożka tworzy z podstawą kąt  , taki, że
, taki, że
A) 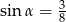 B)
B) 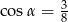 C)
C) 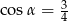 D)
D) 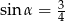
Objętość kuli stycznej do wszystkich ścian sześcianu o krawędzi długości 6 jest równa
A) 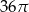 B)
B) 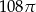 C)
C) 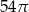 D)
D) 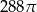
Objętość kuli stycznej do wszystkich ścian sześcianu o krawędzi długości 18 jest równa
A) 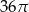 B)
B) 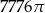 C)
C) 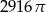 D)
D) 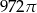
Objętość kuli stycznej do wszystkich ścian sześcianu o krawędzi długości 12 jest równa
A) 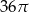 B)
B) 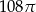 C)
C) 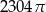 D)
D)