Promień podstawy stożka o objętości 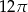 i wysokości 4 jest równy
i wysokości 4 jest równy
A) 1 B) 3 C) 6 D) 9
/Szkoła średnia/Zadania testowe/Geometria/Stereometria
Rysunek przedstawia ostrosłup prawidłowy czworokątny 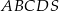 .
.
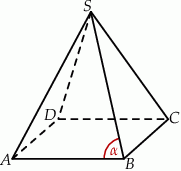
Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy 4. Zatem tangens zaznaczonego kąta 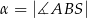 jest równy
jest równy
A) 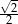 B)
B) 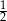 C) 2 D) 4
C) 2 D) 4
Objętość kuli wpisanej w sześcian o krawędzi długości 2 jest równa
A) 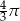 B)
B) 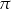 C)
C) 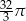 D)
D) 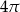
Objętość kuli wpisanej w sześcian o krawędzi długości 4 jest równa
A) 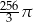 B)
B) 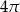 C)
C) 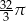 D)
D) 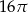
Tworząca stożka o promieniu podstawy 3 ma długość 6 (zobacz rysunek).
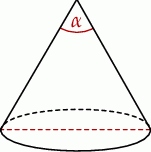
Kąt  rozwarcia tego stożka jest równy
rozwarcia tego stożka jest równy
A) 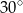 B)
B) 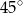 C)
C) 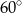 D)
D) 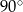
Tworząca stożka o wysokości 3 ma długość 6 (zobacz rysunek).
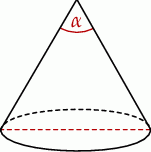
Kąt  rozwarcia tego stożka jest równy
rozwarcia tego stożka jest równy
A) 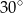 B)
B) 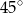 C)
C) 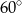 D)
D) 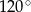
Graniastosłup, który ma 22 ściany, ma
A) 42 wierzchołki B) 22 wierzchołki C) 40 wierzchołków D) 20 wierzchołków
Graniastosłup, który ma 18 ścian, ma
A) 36 wierzchołków B) 32 wierzchołki C) 30 wierzchołków D) 48 wierzchołków
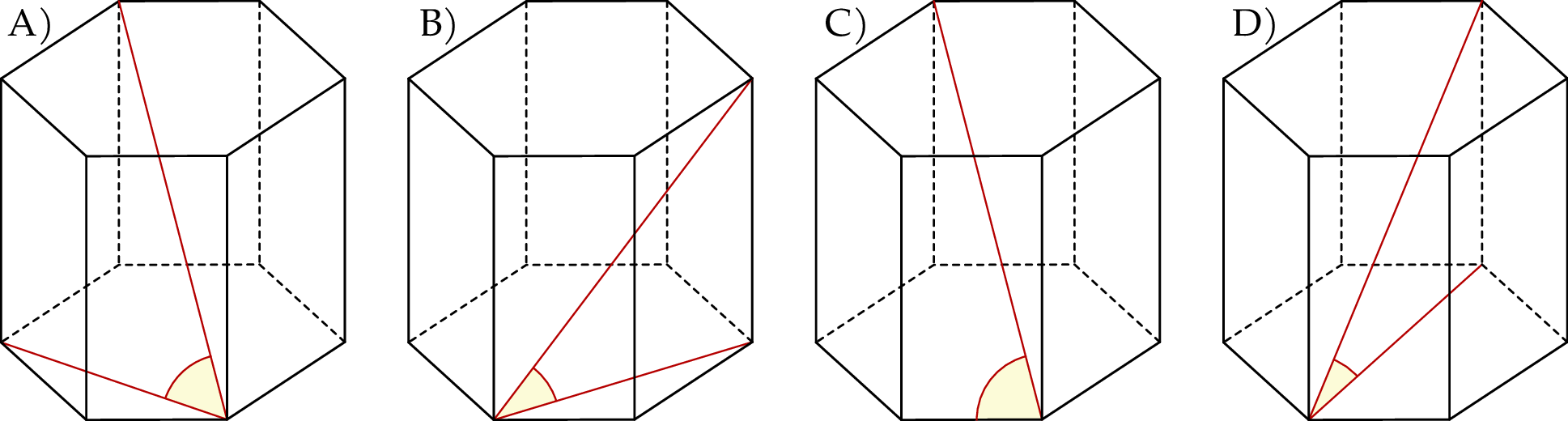
Kąt nachylenia najdłuższej przekątnej graniastosłupa prawidłowego sześciokątnego do płaszczyzny podstawy jest zaznaczony na rysunku
Walec i stożek mają równe promienie podstaw, a wysokość walca jest dwa razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 3 B) 6 C) 2 D) 12
Walec i stożek mają równe promienie podstaw, a wysokość walca jest trzy razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 9 B) 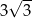 C) 3 D) 27
C) 3 D) 27
Dany jest ostrosłup, którego podstawą jest kwadrat o boku 6. Jedna z krawędzi bocznych tego ostrosłupa ma długość 12 i jest prostopadła do płaszczyzny podstawy. Tangens kąta nachylenia najdłuższej krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy jest równy
A) 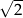 B)
B) 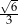 C)
C) 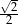 D)
D) 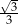
Dwa stożki o takich samych podstawach połączono podstawami z podstawami walca w taki sposób jak na rysunku. Wysokość mniejszego z tych stożków jest taka sama jak wysokość walca i stanowi  wysokości większego ze stożków. Objętość całej bryły jest równa
wysokości większego ze stożków. Objętość całej bryły jest równa 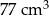 .
.
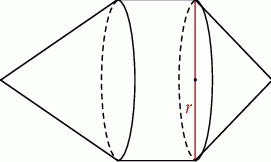
Objętość walca jest równa
A) 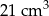 B)
B) 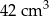 C)
C) 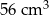 D)
D) 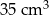
Każda krawędź ostrosłupa prawidłowego trójkątnego ma długość 9 (ostrosłup taki jest nazywany czworościanem foremnym). Wysokość tego ostrosłupa jest równa
A) 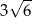 B)
B) 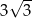 C)
C) 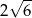 D)
D) 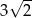
Każda krawędź ostrosłupa prawidłowego trójkątnego ma długość 12 (ostrosłup taki jest nazywany czworościanem foremnym). Wysokość tego ostrosłupa jest równa
A) 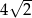 B)
B) 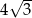 C)
C) 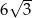 D)
D) 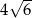
Przekątna graniastosłupa prawidłowego czworokątnego ma długość 10 cm, a krawędź podstawy ma długość 5 cm. Cosinus kąta nachylenia tej przekątnej do podstawy jest równy
A) 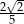 B)
B) 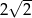 C)
C) 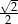 D)
D) 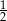
Przekątna graniastosłupa prawidłowego czworokątnego ma długość 6 cm, a krawędź podstawy ma długość 3 cm. Cosinus kąta nachylenia tej przekątnej do podstawy jest równy
A) 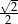 B)
B) 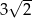 C)
C) 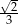 D)
D) 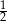
Przekątna graniastosłupa prawidłowego czworokątnego ma długość 9 cm, a krawędź podstawy ma długość 3 cm. Cosinus kąta nachylenia tej przekątnej do podstawy jest równy
A) 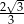 B)
B) 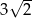 C)
C) 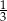 D)
D) 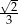
Wysokość graniastosłupa prawidłowego czworokątnego, którego pole powierzchni całkowitej jest równe 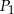 , zwiększono trzykrotnie. Pole powierzchni całkowitej otrzymanego w ten sposób graniastosłupa jest równe
, zwiększono trzykrotnie. Pole powierzchni całkowitej otrzymanego w ten sposób graniastosłupa jest równe 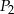 . Zatem
. Zatem
A) 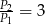 B)
B) 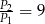 C)
C) 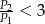 D)
D) 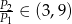
Objętość stożka o wysokości 8 i średnicy podstawy 12 jest równa
A) 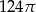 B)
B) 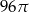 C)
C) 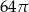 D)
D) 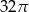
Dany jest stożek o wysokości 5 i średnicy podstawy 6. Objętość tego stożka jest równa
A) 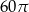 B)
B) 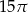 C)
C) 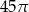 D)
D) 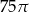
Dany jest stożek o wysokości 4 i średnicy podstawy 12. Objętość tego stożka jest równa
A) 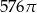 B)
B) 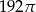 C)
C) 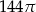 D)
D) 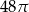
Objętość stożka o wysokości 4 i średnicy podstawy 6 jest równa
A) 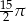 B)
B) 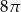 C)
C) 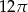 D)
D) 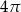
Objętość ostrosłupa prawidłowego trójkątnego o wysokości 8 jest równa 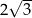 . Długość krawędzi podstawy tego ostrosłupa jest równa
. Długość krawędzi podstawy tego ostrosłupa jest równa
A) 3 B) 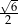 C) 1 D)
C) 1 D) 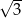
Kula o promieniu 5 cm i stożek o promieniu podstawy 10 cm mają równe objętości. Wysokość stożka jest równa
A) 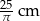 B) 10 cm C)
B) 10 cm C) 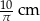 D) 5 cm
D) 5 cm
Pole powierzchni kuli o promieniu 6 cm jest równe polu powierzchni całkowitej stożka o promieniu podstawy 8 cm. Pole powierzchni bocznej stożka jest równe
A) 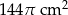 B)
B) 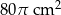 C)
C) 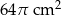 D)
D) 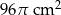
Promień kuli i promień podstawy stożka są równe 4. Pole powierzchni kuli jest równe polu powierzchni całkowitej stożka. Długość tworzącej stożka jest równa
A) 8 B) 4 C) 16 D) 12
Objętość graniastosłupa prawidłowego trójkątnego o wysokości 7 jest równa 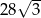 . Długość krawędzi podstawy tego graniastosłupa jest równa
. Długość krawędzi podstawy tego graniastosłupa jest równa
A) 2 B) 4 C) 8 D) 16
Objętość graniastosłupa prawidłowego trójkątnego o wysokości 7 jest równa 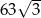 . Długość krawędzi podstawy tego graniastosłupa jest równa
. Długość krawędzi podstawy tego graniastosłupa jest równa
A) 4 B) 3 C) 6 D) 36
Długość tworzącej stożka jest równa 6, a obwód jego podstawy wynosi 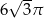 . Kąt rozwarcia tego stożka ma miarę
. Kąt rozwarcia tego stożka ma miarę
A) 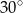 B)
B) 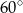 C)
C) 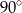 D)
D) 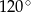
Objętość stożka o promieniu podstawy równym  jest równa
jest równa 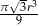 . Miara kąta rozwarcia tego stożka jest równa
. Miara kąta rozwarcia tego stożka jest równa
A) 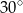 B)
B) 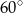 C)
C) 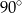 D)
D) 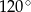
Objętość kuli jest równa 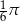 . Pole powierzchni tej kuli wyraża się liczbą
. Pole powierzchni tej kuli wyraża się liczbą
A) wymierną większą od 3 B) wymierną mniejszą od 3
C) niewymierną większą od 3 D) niewymierną mniejszą od 3
Objętość kuli jest równa 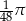 . Pole powierzchni tej kuli wyraża się liczbą
. Pole powierzchni tej kuli wyraża się liczbą
A) wymierną większą od 1 B) wymierną mniejszą od 1
C) niewymierną większą od 1 D) niewymierną mniejszą od 1
Objętość kuli jest równa 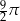 . Pole powierzchni tej kuli wyraża się liczbą
. Pole powierzchni tej kuli wyraża się liczbą
A) niewymierną większą od 27 B) niewymierną mniejszą od 27
C) wymierną mniejszą od 27 D) wymierną większą od 27
Liczba przekątnych sześcianu to
A) 6 B) 12 C) 8 D) 4
Liczba przekątnych wszystkich ścian bocznych i podstaw pewnego graniastosłupa jest równa 110. Zatem podstawą tego graniastosłupa jest:
A) dziewięciokąt B) dziesięciokąt C) jedenastokąt D) dwunastokąt
Liczba przekątnych wszystkich ścian bocznych i podstawy pewnego graniastosłupa jest równa 182. Zatem podstawą tego graniastosłupa jest:
A) trzynastokąt B) czternastokąt C) piętnastokąt D) szesnastokąt
Liczba przekątnych wszystkich ścian bocznych i podstaw pewnego graniastosłupa jest równa 240. Zatem podstawą tego graniastosłupa jest:
A) trzynastokąt B) czternastokąt C) piętnastokąt D) szesnastokąt

