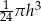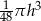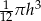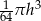Na rysunku przedstawiono bryłę zbudowaną z walca, stożka i półkuli. Wysokość walca jest równa  i jest taka sama jak wysokość stożka, oraz taka sama jak promień półkuli, promień podstawy walca i promień podstawy stożka.
i jest taka sama jak wysokość stożka, oraz taka sama jak promień półkuli, promień podstawy walca i promień podstawy stożka.
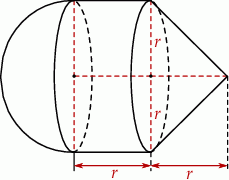
Objętość tej bryły jest równa
A) 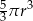 B)
B) 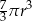 C)
C) 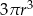 D)
D) 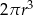

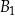 oraz
oraz 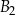 . Objętość prostopadłościanu
. Objętość prostopadłościanu 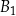 jest równa
jest równa 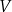 , a objętość prostopadłościanu
, a objętość prostopadłościanu 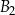 jest równa
jest równa 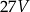 . Pole powierzchni całkowitej prostopadłościanu
. Pole powierzchni całkowitej prostopadłościanu 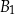 jest równe
jest równe 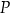 . Pole powierzchni całkowitej prostopadłościanu
. Pole powierzchni całkowitej prostopadłościanu 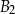 jest równe
jest równe 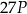 ,
,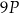 ,
,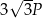
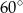 i mniejszą od
i mniejszą od 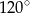
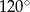 i mniejszą od
i mniejszą od 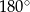
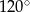
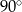 i mniejszą od
i mniejszą od 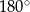
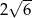 . Objętość tego sześcianu wynosi
. Objętość tego sześcianu wynosi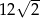
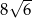
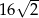
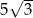 . Wtedy objętość tego sześcianu jest równa
. Wtedy objętość tego sześcianu jest równa 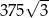
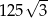
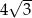 . Objętość tego sześcianu wynosi
. Objętość tego sześcianu wynosi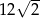
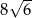
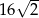
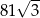
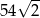
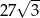
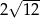 . Objętość tego sześcianu wynosi
. Objętość tego sześcianu wynosi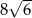
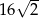
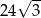
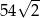
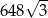
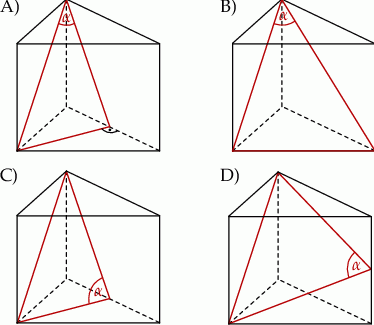
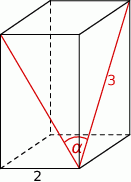
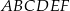 . Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt
. Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt  pomiędzy ścianą boczną
pomiędzy ścianą boczną 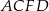 i przekątną
i przekątną 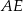 ściany bocznej
ściany bocznej  tego graniastosłupa?
tego graniastosłupa? 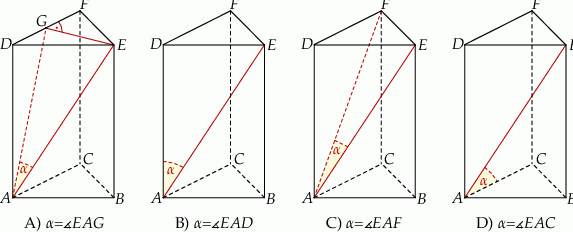
 . Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt
. Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt  pomiędzy ścianą boczną
pomiędzy ścianą boczną  i przekątną
i przekątną 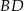 ściany bocznej
ściany bocznej  tego graniastosłupa?
tego graniastosłupa? 
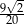
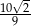
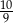
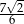
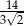
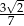
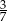
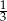
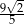
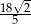
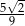
 . Kąt nachylenia krawędzi bocznej do płaszczyzny podstawy czworościanu oznaczono literą:
. Kąt nachylenia krawędzi bocznej do płaszczyzny podstawy czworościanu oznaczono literą: 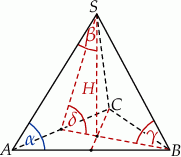

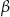
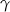
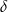
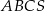 . Kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa oznaczono literą:
. Kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa oznaczono literą: 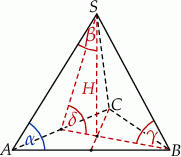

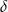
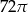 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy 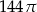 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy 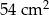 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa 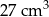
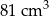
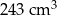
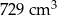
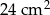 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa 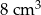
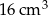
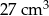
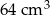
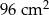 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa 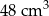
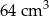
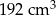
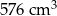
 .
. 
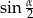 jest równa
jest równa 
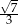
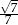
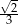
 .
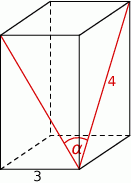
. 
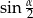 jest równa
jest równa 
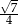
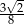
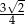
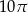
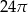
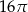
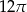
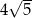 i polu 20. Pole powierzchni bocznej tego walca jest równe
i polu 20. Pole powierzchni bocznej tego walca jest równe 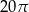
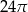
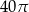
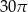
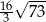
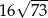
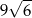
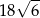
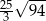
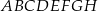 o krawędzi długości
o krawędzi długości  . Punkty
. Punkty 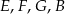 są wierzchołkami ostrosłupa
są wierzchołkami ostrosłupa 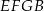 (zobacz rysunek).
(zobacz rysunek). 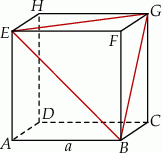
 jest równe
jest równe 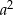
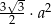
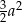
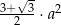
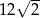
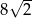
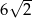
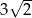
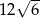
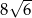
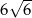
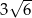
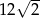
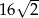
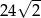
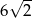
 , w którym bok
, w którym bok 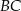 odpowiada krawędzi rozcięcia (wysokości graniastosłupa). Przekątna
odpowiada krawędzi rozcięcia (wysokości graniastosłupa). Przekątna 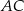 tego prostokąta ma długość 15 i tworzy z bokiem
tego prostokąta ma długość 15 i tworzy z bokiem 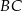 kąt o mierze
kąt o mierze 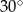 (zobacz rysunek).
(zobacz rysunek). 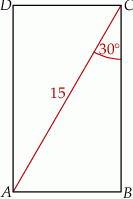
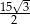
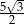
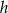 i promieniu podstawy trzy razy mniejszym od wysokości jest równa
i promieniu podstawy trzy razy mniejszym od wysokości jest równa 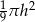
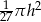
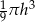
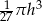
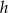 i promieniu podstawy cztery razy mniejszym od wysokości jest równa
i promieniu podstawy cztery razy mniejszym od wysokości jest równa