Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 2 (zobacz rysunek).
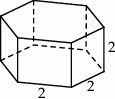
Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 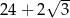 B)
B) 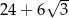 C)
C) 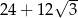 D)
D) 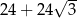
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 2 (zobacz rysunek).

Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 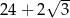 B)
B) 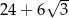 C)
C) 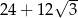 D)
D) 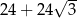
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6. Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 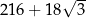 B)
B) 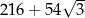 C)
C) 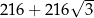 D)
D) 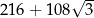
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 3 (zobacz rysunek).
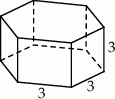
Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 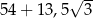 B)
B) 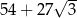 C)
C) 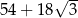 D)
D) 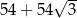
Suma długości wszystkich krawędzi sześcianu jest równa 24. Objętość tego sześcianu jest równa
A) 8 B) 27 C) 24 D) 64
Suma wszystkich krawędzi sześcianu jest równa 36. Objętość tego sześcianu jest równa
A) 8 B) 27 C) 64 D) 24
Suma długości wszystkich krawędzi sześcianu jest równa 72. Objętość tego sześcianu jest równa
A) 1728 B) 216 C) 127 D) 81
Cosinus kąta dwuściennego utworzonego przez dwie sąsiednie ściany czworościanu foremnego jest równy
A) 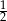 B)
B) 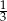 C)
C)  D)
D) 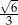
W czworościanie foremnym cosinus kąta dwuściennego między dwiema sąsiednimi ścianami jest równy
A) 0 B) 0,25 C) 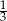 D)
D) 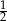
Przekrojem osiowym stożka o objętości 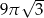 jest trójkąt równoboczny. Obwód tego trójkąta jest równy
jest trójkąt równoboczny. Obwód tego trójkąta jest równy
A) 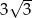 B)
B) 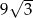 C) 18 D) 6
C) 18 D) 6
Przekrojem prostopadłościanu zawierającym przekątną podstawy i przekątne sąsiednich ścian bocznych wychodzących z tego samego wierzchołka jest
A) kwadrat B) prostokąt C) trójkąt D) trapez
Prostokąt o bokach 4 i 6 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 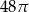 B)
B) 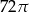 C)
C) 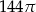 D)
D) 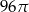
Prostokąt o bokach 10 i 6 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 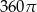 B)
B) 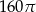 C)
C) 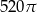 D)
D) 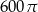
Prostokąt o bokach 3 i 5 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 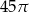 B)
B) 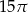 C)
C) 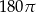 D)
D) 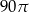
Objętość sześcianu 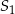 jest równa
jest równa 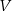 , a objętość sześcianu
, a objętość sześcianu 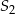 jest równa
jest równa 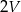 . Pole powierzchni całkowitej sześcianu
. Pole powierzchni całkowitej sześcianu 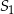 jest równe
jest równe 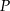 . Pole powierzchni całkowitej sześcianu
. Pole powierzchni całkowitej sześcianu 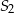 jest równe
jest równe
A) 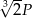 , , | B) 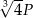 , , |
| ponieważ stosunek pól powierzchni brył podobnych jest równy | |
| 1) | sześcianowi skali podobieństwa. |
| 2) | skali podobieństwa. |
| 3) | kwadratowi skali podobieństwa. |
Obwód podstawy stożka wynosi 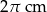 . Tworząca stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego stożka jest równe
. Tworząca stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego stożka jest równe
A) 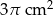 B)
B) 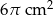 C)
C) 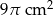 D)
D) 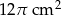
Obwód podstawy stożka wynosi 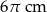 . Tworząca stożka jest 4 razy dłuższa od jego promienia podstawy. Zatem pole powierzchni całkowitej tego stożka jest równe
. Tworząca stożka jest 4 razy dłuższa od jego promienia podstawy. Zatem pole powierzchni całkowitej tego stożka jest równe
A) 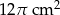 B)
B) 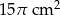 C)
C) 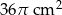 D)
D) 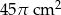
Przekrój osiowy stożka jest trójkątem równobocznym o boku  . Jeżeli
. Jeżeli  oznacza promień podstawy stożka,
oznacza promień podstawy stożka, 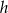 oznacza wysokość, to
oznacza wysokość, to
A) 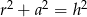 B)
B) 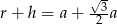 C)
C) 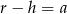 D)
D) 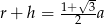
Przekrój osiowy stożka jest trójkątem równobocznym o wysokości 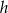 . Jeżeli
. Jeżeli  oznacza promień podstawy stożka,
oznacza promień podstawy stożka, 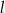 oznacza długość jego tworzącej, to
oznacza długość jego tworzącej, to
A) 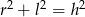 B)
B) 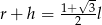 C)
C) 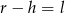 D)
D) 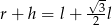
Przekrój osiowy stożka jest trójkątem rozwartokątnym o polu 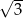 . Jeżeli tworząca tego stożka ma długość 2, to jego objętość jest równa
. Jeżeli tworząca tego stożka ma długość 2, to jego objętość jest równa
A) 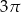 B)
B) 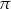 C)
C) 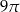 D)
D) 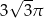
Dany jest trójkąt prostokątny o długościach boków 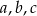 , gdzie
, gdzie 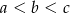 . Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt 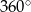 , otrzymujemy bryłę, której objętość jest równa
, otrzymujemy bryłę, której objętość jest równa
A) 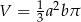 B)
B) 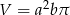 C)
C) 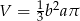 D)
D) 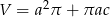
Dany jest trójkąt prostokątny o długościach boków 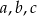 , gdzie
, gdzie 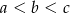 . Obracając ten trójkąt, wokół prostej zawierającej krótszą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej krótszą przyprostokątną o kąt 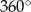 , otrzymujemy bryłę, której objętość jest równa
, otrzymujemy bryłę, której objętość jest równa
A) 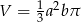 B)
B) 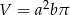 C)
C) 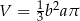 D)
D) 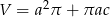
Kąt nachylenia ściany bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy ma miarę 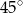 . Krawędź podstawy ma długość 6 cm. Długość wysokości tego ostrosłupa jest równa
. Krawędź podstawy ma długość 6 cm. Długość wysokości tego ostrosłupa jest równa
A) 6 cm B) 3 cm C) 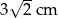 D)
D) 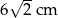
Kąt nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy ma miarę 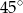 . Krawędź boczna ma długość 12 cm. Długość wysokości tego ostrosłupa jest równa
. Krawędź boczna ma długość 12 cm. Długość wysokości tego ostrosłupa jest równa
A) 6 cm B) 3 cm C) 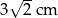 D)
D) 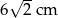
Kąt nachylenia ściany bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy ma miarę 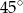 . Wysokość ściany bocznej ma długość 6 cm. Długość wysokości tego ostrosłupa jest równa
. Wysokość ściany bocznej ma długość 6 cm. Długość wysokości tego ostrosłupa jest równa
A) 6 cm B) 3 cm C) 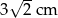 D)
D) 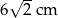
Tworząca stożka ma długość 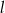 , a promień jego podstawy jest równy
, a promień jego podstawy jest równy  (zobacz rysunek).
(zobacz rysunek).
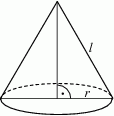
Powierzchnia boczna tego stożka jest 2 razy większa od pola jego podstawy. Wówczas
A) 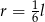 B)
B) 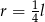 C)
C) 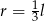 D)
D) 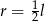
Tworząca stożka ma długość 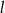 , a promień jego podstawy jest równy
, a promień jego podstawy jest równy  (zobacz rysunek).
(zobacz rysunek).
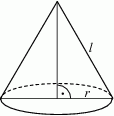
Powierzchnia boczna tego stożka jest 3 razy większa od pola jego podstawy. Wówczas
A) 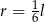 B)
B) 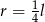 C)
C) 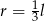 D)
D) 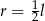
Długości trzech wychodzących z jednego wierzchołka krawędzi prostopadłościanu są trzema kolejnymi liczbami naturalnymi parzystymi. Najdłuższa krawędź tego prostopadłościanu ma długość 10. Pole powierzchni całkowitej tego prostopadłościanu jest równe
A) 376 B) 466 C) 480 D) 720
Prostopadłościan dzielimy na części prowadząc dwie płaszczyzny równoległe do jego podstaw, które dzielą krawędź boczną w stosunku 5:1:2. Jaki procent objętości całego prostopadłościanu stanowi objętość najmniejszej z utworzonych części?
A) 15% B) 25% C) 17% D) 12,5%
Prostopadłościan dzielimy na części prowadząc dwie płaszczyzny równoległe do jego podstaw, które dzielą krawędź boczną w stosunku 5:1:2. Jaki procent objętości całego prostopadłościanu stanowi objętość największej z utworzonych części?
A) 62,5% B) 37,5% C) 65% D) 75%
Każda krawędź graniastosłupa prawidłowego trójkątnego ma długość równą 8. Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 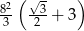 B)
B) 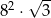 C)
C) 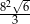 D)
D) 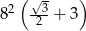
Każda krawędź graniastosłupa prawidłowego trójkątnego ma długość równą 6. Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 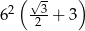 B)
B) 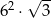 C)
C) 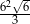 D)
D) 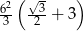
Średnica podstawy stożka ma długość 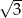 , a jego tworząca ma długość 1. Tangens kąta rozwarcia tego stożka jest równy
, a jego tworząca ma długość 1. Tangens kąta rozwarcia tego stożka jest równy
A) 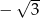 B)
B) 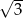 C)
C) 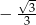 D)
D) 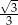
Obwód podstawy walca wynosi 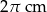 . Wysokość walca jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego walca jest równe
. Wysokość walca jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego walca jest równe
A) 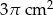 B)
B) 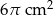 C)
C) 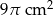 D)
D) 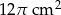
Wycinek kołowy o kącie środkowym 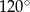 i polu
i polu 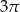 zwinięto w stożek. Promień podstawy tego stożka jest równy:
zwinięto w stożek. Promień podstawy tego stożka jest równy:
A) 2,5 B) 2 C) 1,6 D) 1
Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 15. Przekątna ściany bocznej graniastosłupa jest nachylona do płaszczyzny podstawy pod  takim, że
takim, że 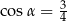 . Długość przekątnej tego graniastosłupa jest równa
. Długość przekątnej tego graniastosłupa jest równa
A) 25 B) 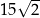 C)
C) 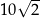 D) 20
D) 20
