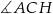Stosunek wysokości stożka do promienia podstawy wynosi 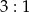 . Objętość stożka jest równa
. Objętość stożka jest równa 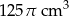 . Zatem promień podstawy stożka ma długość
. Zatem promień podstawy stożka ma długość
A) 25 cm B) 15 cm C) 5 cm D) 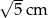
/Szkoła średnia/Zadania testowe/Geometria/Stereometria
Stosunek wysokości stożka do promienia podstawy wynosi 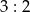 . Objętość stożka jest równa
. Objętość stożka jest równa 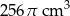 . Zatem promień podstawy stożka ma długość
. Zatem promień podstawy stożka ma długość
A) 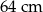 B)
B) 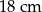 C)
C) 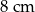 D)
D) 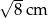
Stosunek wysokości stożka do promienia podstawy wynosi 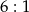 . Objętość stożka jest równa
. Objętość stożka jest równa 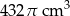 . Zatem promień podstawy stożka ma długość
. Zatem promień podstawy stożka ma długość
A) 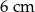 B)
B) 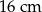 C)
C) 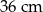 D)
D) 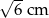
Podstawą ostrosłupa jest kwadrat 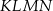 o boku długości 4. Wysokością tego ostrosłupa jest krawędź
o boku długości 4. Wysokością tego ostrosłupa jest krawędź 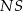 , a jej długość jest równa 6 (zobacz rysunek).
, a jej długość jest równa 6 (zobacz rysunek).
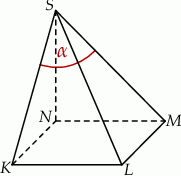
Kąt  , jaki tworzą krawędzie
, jaki tworzą krawędzie 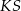 i
i 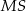 , spełnia warunek
, spełnia warunek
A) 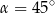 B)
B) 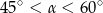 C)
C) 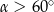 D)
D) 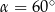
Liczba przekątnych graniastosłupa prawidłowego sześciokątnego jest równa
A) 12 B) 18 C) 6 D) 9
Pewien wielościan ma 6 krawędzi. Liczba jego ścian jest równa
A) 4 B) 5 C) 6 D) 9
Pewien wielościan ma 4 ściany. Liczba jego krawędzi jest równa
A) 4 B) 5 C) 6 D) 9
Jeśli średnica podstawy stożka jest równa 12, a wysokość stożka 8, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 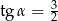 B)
B) 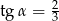 C)
C) 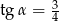 D)
D) 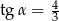
Jeśli średnica podstawy stożka jest równa 18, a wysokość stożka 12, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 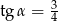 B)
B) 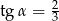 C)
C) 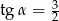 D)
D) 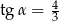
Jeśli średnica podstawy stożka jest równa 16, a wysokość stożka 6, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 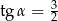 B)
B) 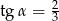 C)
C) 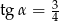 D)
D) 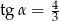
Trójkąt prostokątny równoramienny obrócono dookoła jednej z przyprostokątnych. Objętość tak otrzymanej bryły jest równa 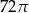 . Średnica podstawy bryły ma długość
. Średnica podstawy bryły ma długość
A) 6 B) 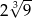 C) 12 D)
C) 12 D) 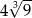
Trójkąt prostokątny równoramienny obrócono dookoła jednej z przyprostokątnych. Objętość tak otrzymanej bryły jest równa 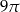 . Średnica podstawy bryły ma długość
. Średnica podstawy bryły ma długość
A) 6 B) 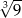 C) 3 D)
C) 3 D) 
Trójkąt prostokątny równoramienny obrócono dookoła jednej z przyprostokątnych. Objętość tak otrzymanej bryły jest równa 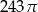 . Średnica podstawy bryły ma długość
. Średnica podstawy bryły ma długość
A) 9 B) 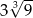 C)
C) 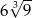 D) 18
D) 18
Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 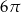 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 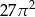 B)
B) 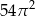 C)
C) 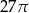 D)
D) 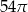
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 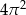 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 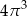 B)
B) 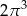 C)
C) 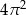 D)
D) 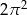
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 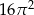 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 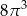 B)
B) 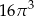 C)
C) 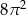 D)
D) 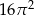
Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 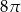 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 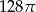 B)
B) 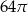 C)
C) 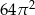 D)
D) 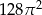
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 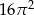 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 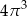 B)
B) 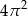 C)
C) 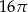 D)
D) 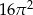
Pole powierzchni całkowitej walca, którego przekrojem osiowym jest kwadrat o boku długości 4, jest równe
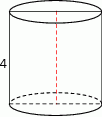
A) 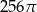 B)
B) 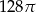 C)
C) 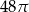 D)
D) 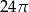
Pole powierzchni całkowitej walca, którego przekrojem osiowym jest kwadrat o boku długości 6, jest równe
A) 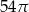 B)
B) 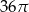 C)
C) 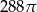 D)
D) 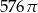
Obwód podstawy ostrosłupa prawidłowego siedmiokątnego jest równy 33,6 cm, a długość jego krawędzi bocznej jest równa 2,5 cm. Pole powierzchni bocznej tego ostrosłupa jest równe
A) 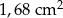 B)
B) 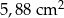 C)
C) 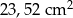 D)
D) 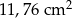
Narysowana bryła ma w podstawie kwadrat, a krawędzie boczne są prostopadłe do podstawy. Objętość tej bryły jest równa
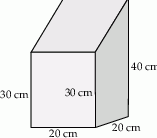
A) 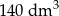 B)
B) 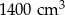 C)
C) 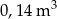 D)
D) 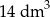
Liczba wszystkich krawędzi graniastosłupa jest równa 24. Wówczas podstawą tego graniastosłupa jest:
A) sześciokąt B) ośmiokąt C) dziesięciokąt D) dwunastokąt
Liczba wszystkich krawędzi graniastosłupa jest równa 21. Wówczas podstawą tego graniastosłupa jest:
A) sześciokąt B) ośmiokąt C) siedmiokąt D) dwunastokąt
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Suma długości wszystkich krawędzi jest równa 90. Wtedy pole powierzchni całkowitej tego graniastosłupa jest równe
A) 300 B) 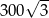 C)
C) 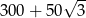 D)
D) 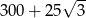
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Suma długości wszystkich krawędzi jest równa 72. Wtedy pole powierzchni całkowitej tego graniastosłupa jest równe
A) 192 B) 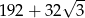 C)
C) 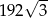 D)
D) 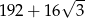
Przekątna podstawy ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości ostrosłupa. Ostrosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i środek jednej z krawędzi bocznych (patrz rysunek).
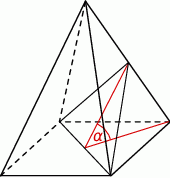
Płaszczyzna przekroju tworzy z podstawą ostrosłupa kąt  o mierze
o mierze
A) 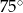 B)
B) 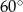 C)
C) 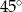 D)
D) 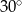
Promień kuli o polu powierzchni równym 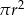 powiększono 2 razy. Objętość tak zmienionej kuli jest równa
powiększono 2 razy. Objętość tak zmienionej kuli jest równa
A) 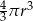 B)
B) 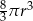 C)
C) 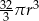 D)
D) 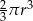
Promień kuli o polu powierzchni równym 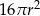 zmniejszono 2 razy. Objętość tak zmienionej kuli jest równa
zmniejszono 2 razy. Objętość tak zmienionej kuli jest równa
A) 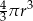 B)
B) 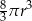 C)
C) 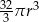 D)
D) 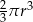
Promień kuli o polu powierzchni równym 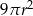 powiększono 2 razy. Objętość tak zmienionej kuli jest równa
powiększono 2 razy. Objętość tak zmienionej kuli jest równa
A) 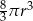 B)
B) 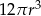 C)
C) 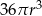 D)
D) 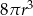
Stosunek pola powierzchni bocznej walca do pola przekroju osiowego tego walca
A) może być większy od 6 B) jest zawsze większy od 3
C) może być równy 3 D) jest zawsze mniejszy od 3
Pewien graniastosłup ma 57 krawędzi. Liczba wszystkich ścian tego graniastosłupa jest równa
A) 19 B) 21 C) 38 D) 57
Ostrosłupy prawidłowe trójkątne 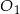 i
i 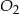 mają takie same wysokości. Długość krawędzi podstawy ostrosłupa
mają takie same wysokości. Długość krawędzi podstawy ostrosłupa 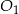 jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa
jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa 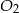 . Stosunek objętości ostrosłupa
. Stosunek objętości ostrosłupa 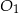 do objętości ostrosłupa
do objętości ostrosłupa 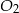 jest równy
jest równy
A) 3 : 1 B) 1 : 3 C) 9 : 1 D) 1 : 9
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość 4, wysokość ostrosłupa ma długość 5. Ściana boczna jest nachylona do podstawy pod kątem  takim, że
takim, że
A) 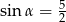 B)
B) 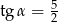 C)
C) 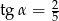 D)
D) 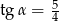
Kąt rozwarcia stożka ma miarę 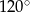 , a jego tworząca ma długość 10. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
, a jego tworząca ma długość 10. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
A) 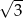 B)
B) 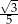 C) 5 D)
C) 5 D) 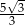
Kąt rozwarcia stożka ma miarę 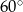 , a jego tworząca ma długość 8. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
, a jego tworząca ma długość 8. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
A) 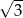 B)
B) 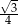 C)
C) 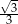 D)
D) 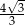
Kąt rozwarcia stożka ma miarę 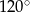 , a jego tworząca ma długość 12. Wówczas stosunek wysokości stożka do jego promienia podstawy jest równy
, a jego tworząca ma długość 12. Wówczas stosunek wysokości stożka do jego promienia podstawy jest równy
A) 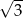 B)
B) 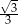 C)
C) 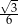 D)
D) 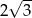
W graniastosłupie prawidłowym sześciokątnym 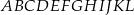 wierzchołki
wierzchołki 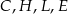 połączono odcinkami (tak jak na rysunku).
połączono odcinkami (tak jak na rysunku).
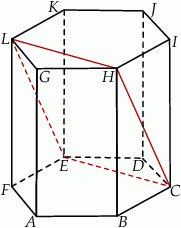
Wskaż kąt między bokiem 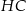 czworokąta
czworokąta 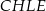 i płaszczyzną podstawy tego graniastosłupa.
i płaszczyzną podstawy tego graniastosłupa.
A) 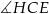 B)
B) 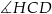 C)
C) 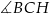 D)
D)