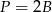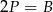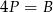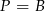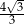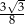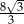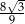Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 4, a przekątna ściany bocznej ma długość 5 (zobacz rysunek). Kąt, jaki tworzą przekątna ściany bocznej i przekątna podstawy wychodzące z jednego wierzchołka, ma miarę  .
.
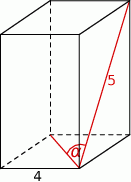
Wtedy wartość 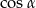 jest równa
jest równa
A)  B)
B) 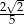 C)
C) 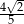 D)
D) 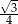

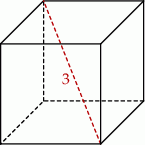
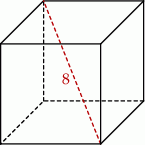
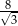
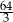
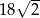
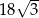
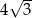 . Pole powierzchni tego sześcianu jest równe
. Pole powierzchni tego sześcianu jest równe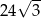
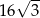
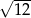 . Pole powierzchni tego sześcianu jest równe
. Pole powierzchni tego sześcianu jest równe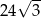
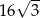
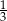
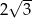
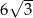
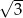
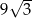
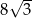
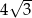
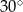 . Każda krawędź tego graniastosłupa ma długość równą 2 (zobacz rysunek).
. Każda krawędź tego graniastosłupa ma długość równą 2 (zobacz rysunek). 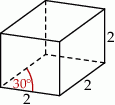
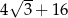
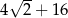
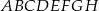 mamy:
mamy: 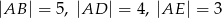 . Który z odcinków
. Który z odcinków 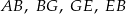 jest najdłuższy?
jest najdłuższy? 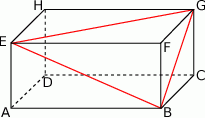
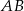
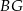
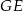
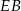
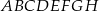 mamy:
mamy: 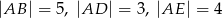 . Który z odcinków
. Który z odcinków 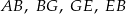 jest najdłuższy?
jest najdłuższy? 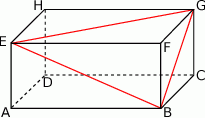
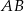
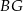
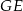
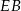
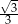
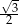
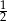
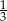
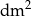 ) i objętość tej kuli (w
) i objętość tej kuli (w 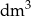 ) wyraża ta sama liczba. Zatem promień tej kuli ma długość
) wyraża ta sama liczba. Zatem promień tej kuli ma długość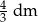
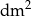 ) jest trzy razy większe niż objętość tej kuli (w
) jest trzy razy większe niż objętość tej kuli (w 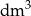 ). Zatem promień tej kuli ma długość
). Zatem promień tej kuli ma długość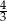 dm
dm 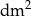 ) jest 4 razy większe od objętość tej kuli (w
) jest 4 razy większe od objętość tej kuli (w 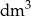 ). Zatem promień tej kuli ma długość
). Zatem promień tej kuli ma długość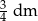
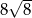 , to przekątna tego sześcianu jest równa
, to przekątna tego sześcianu jest równa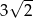
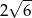
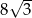
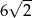
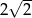 , to przekątna tego sześcianu ma długość
, to przekątna tego sześcianu ma długość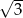
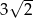
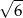
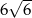 , to przekątna tego sześcianu ma długość
, to przekątna tego sześcianu ma długość 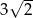
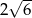
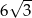
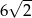
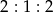 . Przekątna prostopadłościanu ma długość 6. Pole podstawy prostopadłościanu jest równe
. Przekątna prostopadłościanu ma długość 6. Pole podstawy prostopadłościanu jest równe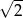
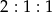 . Przekątna prostopadłościanu ma długość 6. Pole podstawy prostopadłościanu jest równe
. Przekątna prostopadłościanu ma długość 6. Pole podstawy prostopadłościanu jest równe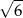
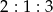 . Przekątna prostopadłościanu ma długość 14. Pole podstawy prostopadłościanu jest równe
. Przekątna prostopadłościanu ma długość 14. Pole podstawy prostopadłościanu jest równe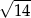
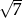
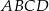 , w którym bok
, w którym bok 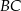 odpowiada krawędzi rozcięcia (wysokości graniastosłupa). Przekątna
odpowiada krawędzi rozcięcia (wysokości graniastosłupa). Przekątna 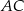 tego prostokąta ma długość 16 i tworzy z bokiem
tego prostokąta ma długość 16 i tworzy z bokiem 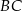 kąt o mierze
kąt o mierze 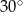 (zobacz rysunek).
(zobacz rysunek). 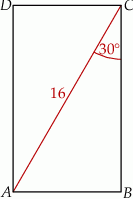
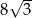
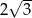
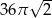
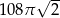
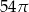
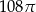
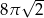
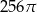
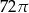
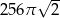
 , którego podstawą jest kwadrat
, którego podstawą jest kwadrat 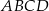 , i w którym krawędź
, i w którym krawędź 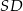 jest prostopadła do płaszczyzny podstawy (patrz rysunek).
jest prostopadła do płaszczyzny podstawy (patrz rysunek). 
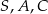
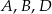
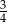
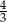
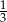
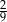
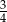
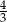
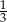
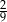
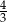
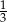
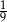
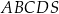 o podstawie
o podstawie 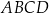 . Długość krawędzi podstawy tego ostrosłupa jest równa 4. Pole powierzchni całkowitej tego ostrosłupa jest równe 56. Wysokość ściany bocznej poprowadzona z wierzchołka
. Długość krawędzi podstawy tego ostrosłupa jest równa 4. Pole powierzchni całkowitej tego ostrosłupa jest równe 56. Wysokość ściany bocznej poprowadzona z wierzchołka 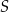 do krawędzi podstawy
do krawędzi podstawy 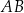 tego ostrosłupa jest równa
tego ostrosłupa jest równa 
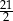
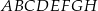 . Przekątne
. Przekątne 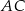 i
i 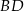 ściany
ściany 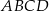 sześcianu przecinają się w punkcie
sześcianu przecinają się w punkcie 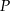 (zobacz rysunek).
(zobacz rysunek). 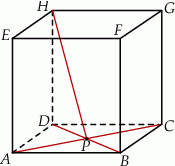
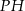 tworzy z płaszczyzną
tworzy z płaszczyzną 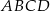 , jest równy
, jest równy 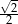
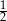
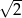
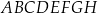 . Przekątne
. Przekątne 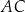 i
i 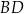 ściany
ściany 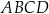 sześcianu przecinają się w punkcie
sześcianu przecinają się w punkcie 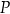 (zobacz rysunek).
(zobacz rysunek). 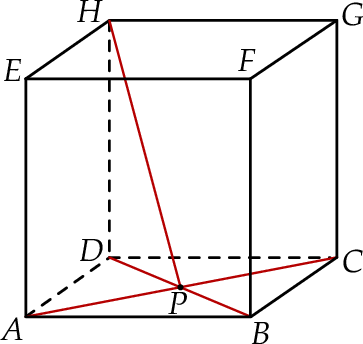
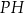 tworzy z krawędzią
tworzy z krawędzią 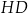 , jest równy
, jest równy 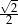
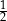
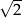
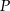 oznacza sumę pól podstaw tego walca, zaś
oznacza sumę pól podstaw tego walca, zaś 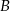 pole jego powierzchni bocznej, to
pole jego powierzchni bocznej, to 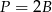
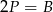
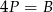
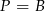
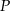 oznacza sumę pól podstaw tego walca, zaś
oznacza sumę pól podstaw tego walca, zaś 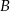 pole jego powierzchni bocznej, to
pole jego powierzchni bocznej, to