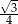Przekątna sześcianu ma długość 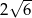 . Suma długości wszystkich krawędzi tego sześcianu wynosi
. Suma długości wszystkich krawędzi tego sześcianu wynosi
A) 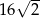 B)
B) 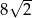 C)
C) 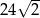 D) 48
D) 48
/Szkoła średnia/Zadania testowe/Geometria/Stereometria
Powierzchnia boczna stożka o promieniu podstawy 6 cm, po rozwinięciu jest wycinkiem koła o kącie 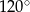 . Pole powierzchni bocznej tego stożka jest równe
. Pole powierzchni bocznej tego stożka jest równe
A) 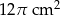 B)
B) 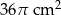 C)
C) 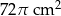 D)
D) 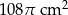
Dany jest prostopadłościan o wymiarach 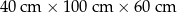 . Jeżeli każdą z najdłuższych krawędzi tego prostopadłościanu wydłużymy o 30%, a każdą z najkrótszych krawędzi skrócimy o 20%, to w wyniku obu tych przekształceń objętość tego prostopadłościanu
. Jeżeli każdą z najdłuższych krawędzi tego prostopadłościanu wydłużymy o 30%, a każdą z najkrótszych krawędzi skrócimy o 20%, to w wyniku obu tych przekształceń objętość tego prostopadłościanu
A) zwiększy się o 8% B) zwiększy się o 4%
C) zmniejszy się o 8% D) zmniejszy się o 4%
Przekrój osiowy stożka jest trójkątem równobocznym o boku  . Objętość tego stożka wyraża się wzorem
. Objętość tego stożka wyraża się wzorem
A) 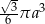 B)
B) 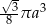 C)
C) 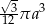 D)
D) 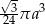
Przekrój osiowy stożka jest równoramiennym trójkątem prostokątnym o przyprostokątnej długości  . Objętość tego stożka wyraża się wzorem
. Objętość tego stożka wyraża się wzorem
A) 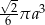 B)
B) 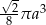 C)
C) 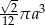 D)
D) 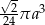
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 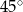 , a wysokość ostrosłupa jest równa 6. Wysokość podstawy tego ostrosłupa ma długość
, a wysokość ostrosłupa jest równa 6. Wysokość podstawy tego ostrosłupa ma długość
A) 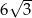 B) 9 C) 12 D)
B) 9 C) 12 D) 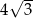
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 7 i 3. Kąt  , jaki przekątna tego graniastosłupa tworzy z jedną z krawędzi górnej podstawy jest równy
, jaki przekątna tego graniastosłupa tworzy z jedną z krawędzi górnej podstawy jest równy 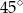 (zobacz rysunek).
(zobacz rysunek).
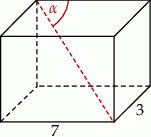
Wysokość graniastosłupa jest równa
A) 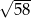 B)
B) 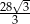 C)
C) 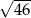 D)
D) 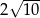
Przekrój osiowy stożka jest trójkątem prostokątnym o przeciwprostokątnej długości 6. Objętość tego stożka jest równa
A) 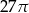 B)
B) 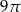 C)
C) 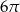 D)
D) 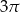
Przekrój osiowy stożka jest trójkątem prostokątnym o przeciwprostokątnej długości 8. Objętość tego stożka jest równa
A) 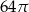 B)
B) 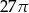 C)
C) 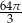 D)
D) 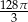
Różnica liczby krawędzi i liczby wierzchołków ostrosłupa jest równa 11. Podstawą tego ostrosłupa jest
A) dziesięciokąt. B) jedenastokąt. C) dwunastokąt. D) trzynastokąt.
W pewnym ostrosłupie prawidłowym stosunek liczby 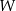 wszystkich wierzchołków do liczby
wszystkich wierzchołków do liczby 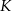 wszystkich krawędzi jest równy
wszystkich krawędzi jest równy 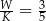 . Podstawą tego ostrosłupa jest
. Podstawą tego ostrosłupa jest
A) kwadrat. B) pięciokąt foremny.
C) sześciokąt foremny. D) siedmiokąt foremny.
W pewnym ostrosłupie prawidłowym stosunek liczby 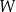 wszystkich wierzchołków do liczby
wszystkich wierzchołków do liczby 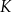 wszystkich krawędzi jest równy
wszystkich krawędzi jest równy 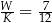 . Podstawą tego ostrosłupa jest
. Podstawą tego ostrosłupa jest
A) kwadrat. B) pięciokąt foremny.
C) sześciokąt foremny. D) siedmiokąt foremny.
Różnica liczby krawędzi i liczby wierzchołków ostrosłupa jest równa 10. Podstawą tego ostrosłupa jest
A) dziesięciokąt. B) jedenastokąt. C) dwunastokąt. D) trzynastokąt.
Podstawą ostrosłupa jest kwadrat 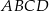 o boku długości 4. Krawędź boczna
o boku długości 4. Krawędź boczna 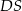 jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
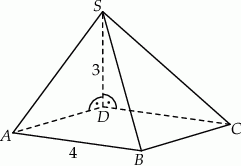
Pole ściany  tego ostrosłupa jest równe
tego ostrosłupa jest równe
A) 20 B) 10 C) 16 D) 12
Podstawą ostrosłupa jest kwadrat  o boku długości 12. Krawędź boczna
o boku długości 12. Krawędź boczna  jest prostopadła do podstawy i ma długość 9 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 9 (zobacz rysunek).
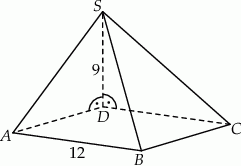
Pole ściany 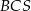 tego ostrosłupa jest równe
tego ostrosłupa jest równe
A) 180 B) 108 C) 54 D) 90
Iloczyn długości wszystkich krawędzi sześcianu jest równy 16. Objętość tego sześcianu jest równa
A) 12 B) 2 C) 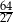 D)
D) 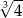
Graniastosłup o podstawie ośmiokąta ma dokładnie
A) 16 wierzchołków. B) 9 wierzchołków. C) 16 krawędzi. D) 8 krawędzi.
Graniastosłup o podstawie dziewięciokąta ma dokładnie
A) 16 wierzchołków. B) 18 wierzchołków. C) 24 krawędzie. D) 18 krawędzi.
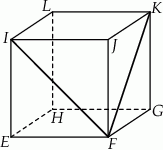
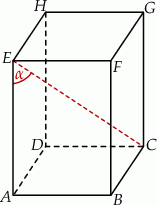
W sześcianie 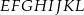 poprowadzono z wierzchołka
poprowadzono z wierzchołka 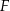 dwie przekątne sąsiednich ścian,
dwie przekątne sąsiednich ścian, 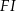 oraz
oraz 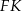 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 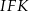 jest równa
jest równa
A) 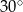 B)
B) 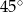 C)
C) 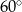 D)
D) 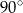
Pole powierzchni bocznej graniastosłupa prawidłowego trójkątnego o wysokości 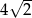 i długości krawędzi przy podstawie równej 4 wynosi
i długości krawędzi przy podstawie równej 4 wynosi
A) 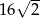 B)
B) 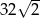 C)
C) 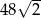 D)
D) 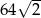
Objętość stożka wynosi 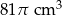 . Wysokość stożka jest 9 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
. Wysokość stożka jest 9 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
A) 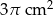 B)
B) 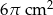 C)
C) 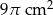 D)
D) 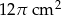
Objętość stożka wynosi 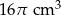 . Wysokość stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
. Wysokość stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
A) 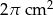 B)
B) 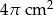 C)
C) 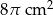 D)
D) 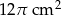
Powierzchnia boczna walca po rozwinięciu na płaszczyznę jest kwadratem o polu 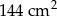 . Jeśli przyjmiemy
. Jeśli przyjmiemy 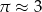 , to promień podstawy walca będzie równy około
, to promień podstawy walca będzie równy około
A) 4 cm B) 2 cm C) 12 cm D) 6 cm
Powierzchnia boczna walca po rozwinięciu na płaszczyznę jest kwadratem o polu 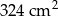 . Jeśli przyjmiemy
. Jeśli przyjmiemy 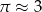 , to promień podstawy walca będzie równy około
, to promień podstawy walca będzie równy około
A) 3 cm B) 9 cm C) 6 cm D) 12 cm
Powierzchnia boczna walca po rozwinięciu na płaszczyznę jest kwadratem o polu 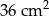 . Jeśli przyjmiemy
. Jeśli przyjmiemy 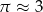 , to promień podstawy walca będzie równy około
, to promień podstawy walca będzie równy około
A) 3 cm B) 12 cm C) 6 cm D) 1 cm
Podstawą graniastosłupa prostego czworokątnego  jest kwadrat
jest kwadrat  o polu 4 (zobacz rysunek). Objętość graniastosłupa jest równa
o polu 4 (zobacz rysunek). Objętość graniastosłupa jest równa 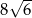 . Miara kąta
. Miara kąta  jest równa
jest równa
A) 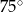 B)
B) 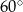 C)
C) 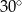 D)
D) 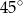
Objętość walca, w którym wysokość jest trzykrotnie dłuższa od promienia podstawy, jest równa 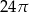 . Zatem promień podstawy tego walca jest ma długość:
. Zatem promień podstawy tego walca jest ma długość:
A) 4 B) 8 C) 2 D) 6
Dany jest walec, w którym wysokość jest równa promieniowi podstawy. Objętość tego walca jest równa 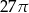 . Wynika stąd, że promień podstawy tego walca jest równy
. Wynika stąd, że promień podstawy tego walca jest równy
A) 9 B) 6 C) 3 D) 2
Objętość walca, w którym wysokość jest trzykrotnie krótsza od promienia podstawy, jest równa 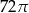 . Zatem promień podstawy tego walca ma długość:
. Zatem promień podstawy tego walca ma długość:
A) 4 B) 8 C) 2 D) 6
Pole powierzchni bocznej stożka wynosi 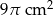 . Tworząca stożka jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
. Tworząca stożka jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
A) 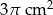 B)
B) 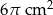 C)
C) 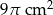 D)
D) 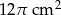
W graniastosłupie prawidłowym czworokątnym 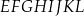 wierzchołki
wierzchołki 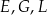 połączono odcinkami (tak jak na rysunku).
połączono odcinkami (tak jak na rysunku).
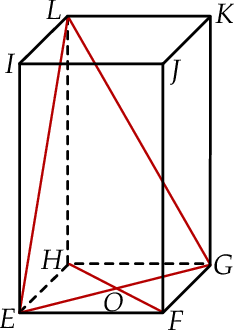
Wskaż kąt między wysokością 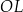 trójkąta
trójkąta 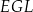 i płaszczyzną podstawy tego graniastosłupa.
i płaszczyzną podstawy tego graniastosłupa.
A) 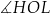 B)
B) 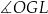 C)
C) 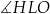 D)
D) 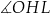
W graniastosłupie prawidłowym czworokątnym  wierzchołki
wierzchołki  połączono odcinkami (tak jak na rysunku).
połączono odcinkami (tak jak na rysunku).
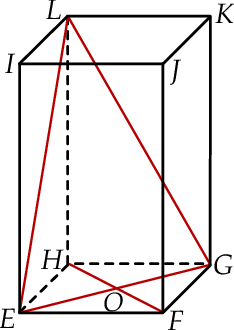
Wskaż kąt między wysokością 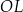 trójkąta
trójkąta 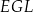 i krawędzią boczną tego graniastosłupa.
i krawędzią boczną tego graniastosłupa.
A) 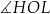 B)
B) 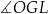 C)
C) 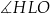 D)
D) 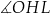
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 4, a przekątna ściany bocznej ma długość 5 (zobacz rysunek). Kąt, jaki tworzą przekątna ściany bocznej i przekątna podstawy wychodzące z jednego wierzchołka, ma miarę  .
.
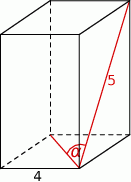
Wtedy wartość 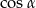 jest równa
jest równa
A)  B)
B) 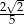 C)
C) 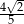 D)
D)